Předpoklad o přímé úměrnosti mezi napětím a deformací lze nejobecněji vyjádřit vztahem
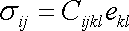 , , |
(2,1) |
který
udává, že složky
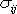 tenzoru napětí jsou lineární kombinací
složek
tenzoru napětí jsou lineární kombinací
složek
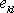 tenzoru deformace. Rovnice
(2,1)
je
nejobecnějším tvarem Hookova zákona.
Koeficienty
tenzoru deformace. Rovnice
(2,1)
je
nejobecnějším tvarem Hookova zákona.
Koeficienty
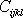 v rovnici
(2,1)
vystihují vlastnosti
látky, budeme jim říkat elastické
koeficienty. Rovnice
(2,1)
platí v každém bodě uvažované látky. Je-li
látka homogenní, tj. má-li ve všech svých bodech stejné vlastnosti, budou při
dané orientaci souřadnicových os hodnoty jednotlivých koeficientů
v rovnici
(2,1)
vystihují vlastnosti
látky, budeme jim říkat elastické
koeficienty. Rovnice
(2,1)
platí v každém bodě uvažované látky. Je-li
látka homogenní, tj. má-li ve všech svých bodech stejné vlastnosti, budou při
dané orientaci souřadnicových os hodnoty jednotlivých koeficientů
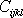 v celé látce stejné.
v celé látce stejné.
Složky
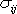 a
a
 jsou složkami tenzoru, potom též koeficienty
jsou složkami tenzoru, potom též koeficienty
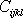 musí být složkami tenzoru a to tenzoru
čtvrtého řádu (viz [1], čl.
5.3 ). Kdyby byly všechny složky vzájemně nezávislé, bylo by jich 34, tj. 81. Jelikož
musí být složkami tenzoru a to tenzoru
čtvrtého řádu (viz [1], čl.
5.3 ). Kdyby byly všechny složky vzájemně nezávislé, bylo by jich 34, tj. 81. Jelikož
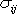 a
a
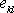 jsou symetrické tenzory, musí být
tenzor
jsou symetrické tenzory, musí být
tenzor
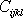 symetrický v indexech i,j a k,l, počet nezávislých koeficientů se
tak redukuje na 62 = 36.
Z energetických úvah ( [1], čl. 6.1 ) plyne, že elastické koeficienty
symetrický v indexech i,j a k,l, počet nezávislých koeficientů se
tak redukuje na 62 = 36.
Z energetických úvah ( [1], čl. 6.1 ) plyne, že elastické koeficienty
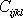 jsou symetrické i při záměně první dvojice
indexů s druhou;
jsou symetrické i při záměně první dvojice
indexů s druhou;
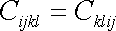 . . |
(2,2) |
Pro 6 z
36 koeficientů je rovnice
(2,2)
splněna automaticky, pro zbývajících
30 dává relace vždy mezi dvěma
koeficienty, čímž snižuje počet nezávislých z
30 na 15. Zbývá tedy 6 + 15 =
21 nezávislých elastických
koeficientů
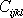 .
Těchto 21 konstant vystihuje elastické chování krystalů trojklonné
(triklinické) soustavy.
.
Těchto 21 konstant vystihuje elastické chování krystalů trojklonné
(triklinické) soustavy.

Trojklonná soustava má nejmenší počet prvků symetrie (např. [5], čl.
4.4 ). Se stoupajícím počtem prvků symetrie počet nezávislých elastických
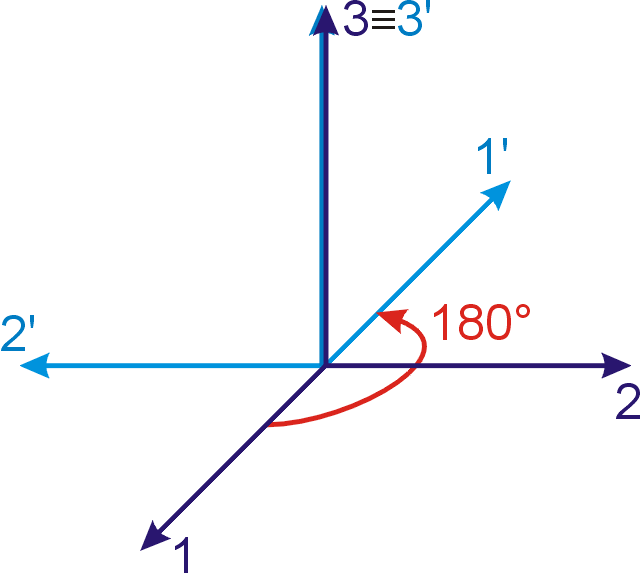
konstant klesá. Krystaly jednoklonné (monoklinické) sousta-vy mají dvojčetnou
osu symetrie. Fyzikální vlastnosti, tedy i elastické koeficienty, musí být
stejné, provedeme-li kolem této osy rotaci o
180o (viz obr.21).
Elastické koeficienty
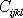 a
a
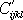 se stejný-mi indexy musí mít v obou
sousta-vách stejné hodnoty. Koeficienty
se stejný-mi indexy musí mít v obou
sousta-vách stejné hodnoty. Koeficienty
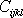 jsou však složkami tenzoru, a proto pro ně
platí transformační rovnice (I6,44),
které pro tenzor čtvrtého řádu mají tvar
jsou však složkami tenzoru, a proto pro ně
platí transformační rovnice (I6,44),
které pro tenzor čtvrtého řádu mají tvar
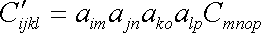 . . |
(2,3) |
Jak již bylo uvedeno v textu k rovnici (I6,44), výrazy
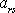 jsou složky (s je proměnný index)
jednotkového vektoru, který leží ve směru a smyslu r-té osy čárkované soustavy souřadnic vyjádřené
v nečárkované soustavě souřadnic. Pro transformaci souřadnic znázorněnou
na obr.21 nabývají z výrazů
jsou složky (s je proměnný index)
jednotkového vektoru, který leží ve směru a smyslu r-té osy čárkované soustavy souřadnic vyjádřené
v nečárkované soustavě souřadnic. Pro transformaci souřadnic znázorněnou
na obr.21 nabývají z výrazů
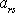 nenulových hodnot pouze
nenulových hodnot pouze
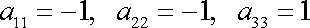 . . |
(2,4) |
Součty na pravé straně rovnice
(2,3)
se pak redukují na
jediný sčítanec, např. pro složku
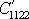 dostáváme vyjádření
dostáváme vyjádření
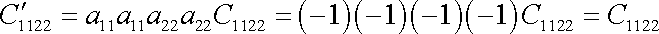 . . |
(2,5) |
Rovnice
(2,5)
nepřináší žádnou redukci počtu elastických
koeficientů, protože odpovídá požadované identičnosti elastických koeficientů
se stejnými indexy v obou uvažovaných souřadnicových soustavách.
Vyskytne-li se však v transformační rovnici
(2,3)
člen
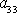 v lichém počtu, dostaneme rovnice
požadující rovnost čárkovaných a nečárkovaných koeficientů
v lichém počtu, dostaneme rovnice
požadující rovnost čárkovaných a nečárkovaných koeficientů
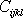 s opačnými znaménky, např.
s opačnými znaménky, např.
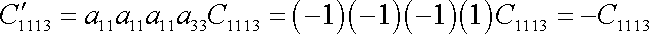 . . |
(2,6) |
Má-li však dle požadavků symetrie krystalu platit
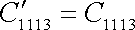 , , |
(2,7) |
lze podmínky (2,6) a (2,7) současně splnit jen, když položíme
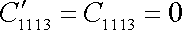 . . |
Nezávislých elastických koeficientů obsahujících lichý počet
trojek je osm:
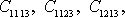
 .
Podmínky
(2,6)
a
(2,7)
tedy sníží počet nezávislých elastických koeficientů
krystalů jednoklonné soustavy o osm oproti krystalům trojklonné soustavy. Počet
elastických koeficientů určujících chování hookovského trojklonného krystalu je 21, pro jednoklonnou soustavu je tento
počet
.
Podmínky
(2,6)
a
(2,7)
tedy sníží počet nezávislých elastických koeficientů
krystalů jednoklonné soustavy o osm oproti krystalům trojklonné soustavy. Počet
elastických koeficientů určujících chování hookovského trojklonného krystalu je 21, pro jednoklonnou soustavu je tento
počet
 .
Počet nezávislých elastických koeficientů krystalových soustav vyšších symetrií
je nižší, pro krychlovou soustavu se redukuje na tři nezávislé koeficienty.
(Počty nezávislých elastických koeficientů pro různé krystalové soustavy jsou
uvedeny např. v [1], čl.
5.3 ).
.
Počet nezávislých elastických koeficientů krystalových soustav vyšších symetrií
je nižší, pro krychlovou soustavu se redukuje na tři nezávislé koeficienty.
(Počty nezávislých elastických koeficientů pro různé krystalové soustavy jsou
uvedeny např. v [1], čl.
5.3 ).
Pro izotropní látku (těleso) se počet nezávislých elastických koeficientů redukuje na dva. V teoretických úvahách bývají jako nezávislé voleny Laméovy konstanty l a m. V technické praxi a při vyhodnocování měření [6] se spíše užívá modulu pružnosti v tahu (Youngova modulu) E a modulu pružnosti ve smyku G, který je totožný s Laméovou konstantou m .
Užijeme-li Laméových konstant pro charakteristiku elastických vlastností izotropní látky, redukuje se rovnice (2,1) na tvar (např. [1], čl. 5,3 )
Rovnice
(2,8)
se nazývá zobecněný Hookův zákon pro izotropní
látku. Zopakujeme (srov.
(1,104)
), že
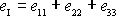 je první invariant tenzoru malých deformací
a
je první invariant tenzoru malých deformací
a
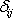 Kroneckerův symbol zavedený v poznámce
na str. 12.
Kroneckerův symbol zavedený v poznámce
na str. 12.
Jsou-li elastické vlastnosti látky popsány moduly E a G, zobecněný Hookův zákon je vyjádřen rovnicí
Zobecněný Hookův zákon pro izotropní prostředí lze odvodit též z představy, že deformace izotropní látky se skládá ze dvou nezávislých částí, z deformace objemové a deformace tvarové. Odvození zde podrobně probereme.
Nejprve ukážeme, že první invariant
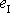 tenzoru je v přiblížení malých
deformací, které vždy při užití tenzoru
tenzoru je v přiblížení malých
deformací, které vždy při užití tenzoru
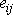 předpokládáme, roven relativní změně objemu.
V diferenciálním okolí bodu, v němž známe složky tenzoru
předpokládáme, roven relativní změně objemu.
V diferenciálním okolí bodu, v němž známe složky tenzoru
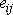 ,
uvažujeme kvádr, jehož hrany délky
,
uvažujeme kvádr, jehož hrany délky
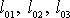 jsou před deformací rovnoběžné se směry
hlavních os deformace. Uvažovaný kvádr zůstane kvádrem i po deformaci, pouze
délky jeho hran se změní na hodnoty
jsou před deformací rovnoběžné se směry
hlavních os deformace. Uvažovaný kvádr zůstane kvádrem i po deformaci, pouze
délky jeho hran se změní na hodnoty
 .
Relativní prodloužení hrany rovnoběžné s první osou je dle
(1,58)
dáno
výrazem
.
Relativní prodloužení hrany rovnoběžné s první osou je dle
(1,58)
dáno
výrazem
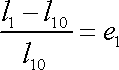 . . |
(2,10) |
Zvolíme-li totiž souřadnicovou soustavu ve směru hlavních os
deformace, hlavní deformace
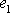 je složkou
je složkou
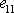 tenzoru uvažovanou v rovnici
(1,58)
.
Rovnice analogické rovnici
(2,10)
pro druhé dva hlavní směry deformace mají
tvar
tenzoru uvažovanou v rovnici
(1,58)
.
Rovnice analogické rovnici
(2,10)
pro druhé dva hlavní směry deformace mají
tvar
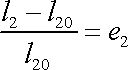 |
(2,10´) |
a
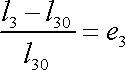 . . |
(2,10´´) |
Vyjádříme-li délky hran kvádru po deformaci, dostaneme
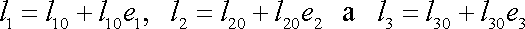 . . |
(2,11) |
Objem V kvádru po deformaci je pak dán výrazem
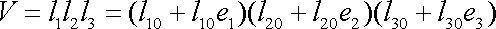 . . |
(2,12) |
Roznásobíme závorky a zanedbáme jako malé veličiny vyšších řádů členy, v kterých se složky tenzoru malých deformací vyskytují více než jednou. Po úpravě dostaneme
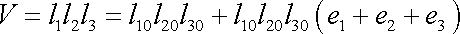 . . |
(2,13) |
Jelikož
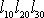 je původní objem
je původní objem
 kvádru a výraz
kvádru a výraz
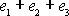 je první invariant
je první invariant
 tenzoru malých deformací, můžeme konečně
psát rovnici
tenzoru malých deformací, můžeme konečně
psát rovnici
která ukazuje, že první invariant
 je v přiblížení užívaném v teorii
malých deformací roven relativní změně objemu
je v přiblížení užívaném v teorii
malých deformací roven relativní změně objemu
 ,
tedy veličině, kterou označujeme jako objemovou
deformaci.
,
tedy veličině, kterou označujeme jako objemovou
deformaci.
Pro tvrzení
(2,14)
není podstatné, že jsme invariant
počítali v soustavě souřadnic proložené hlavními osami tenzoru deformace.
Invariant
 můžeme spočítat jako součet
můžeme spočítat jako součet
 složek se stejnými indexy tenzoru
složek se stejnými indexy tenzoru
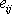 vyjádřeného v libovolné kartézské
soustavě souřadnic a právě vzhledem k tomu, že se jedná o invariant, bude
pro daný bod mít vždy stejnou hodnotu rovnou relativní změně objemu
v okolí tohoto bodu.
vyjádřeného v libovolné kartézské
soustavě souřadnic a právě vzhledem k tomu, že se jedná o invariant, bude
pro daný bod mít vždy stejnou hodnotu rovnou relativní změně objemu
v okolí tohoto bodu.
Užijeme-li invariant
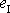 lze tenzor
lze tenzor
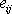 rozložit dle zřejmé identity
rozložit dle zřejmé identity
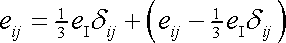 |
(2,15) |
na dvě části, z nichž první označíme
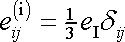 |
(2,16) |
a druhou
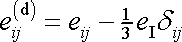 . . |
(2,17) |
Část
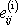 budeme nazývat izotropní část tenzoru malých deformací a část
budeme nazývat izotropní část tenzoru malých deformací a část
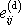 deviátor
tenzoru malých deformací. Dle schématu
(2,15)
lze rozložit na izotropní část a
deviátor každý tenzor druhého řádu. Izotropní část tenzoru
deviátor
tenzoru malých deformací. Dle schématu
(2,15)
lze rozložit na izotropní část a
deviátor každý tenzor druhého řádu. Izotropní část tenzoru
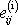 má dle
(2,16)
v libovolné soustavě
souřadnic nenulové pouze složky se shodnými indexy a všechny tyto složky mají
stejnou velikost
má dle
(2,16)
v libovolné soustavě
souřadnic nenulové pouze složky se shodnými indexy a všechny tyto složky mají
stejnou velikost
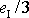 ;
;
 .
Takovému tenzoru odpovídá ve všech směrech stejné relativní prodloužení o
velikosti
.
Takovému tenzoru odpovídá ve všech směrech stejné relativní prodloužení o
velikosti
 ,
smykové úhly jsou nulové, tvar objemových elementů se deformací nemění (viz
úvahy na konci čl. 1.2 ). První invariant
,
smykové úhly jsou nulové, tvar objemových elementů se deformací nemění (viz
úvahy na konci čl. 1.2 ). První invariant
 izotropní části
izotropní části
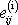 tenzoru
tenzoru
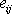 je shodný s prvním invariantem
je shodný s prvním invariantem
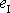 celého tenzoru
celého tenzoru
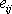 ;
;
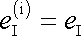 . . |
(2,18) |
Relativní objemová změna odpovídající izotropní části
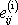 tenzoru malých deformací
tenzoru malých deformací
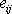 je rovna objemové změně odpovídající celému
tenzoru
je rovna objemové změně odpovídající celému
tenzoru
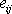 .
.
První invariant deviátoru
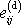 tenzoru
tenzoru
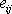 ,
který vypočteme dle definiční rovnice
(2,17)
,
,
který vypočteme dle definiční rovnice
(2,17)
,
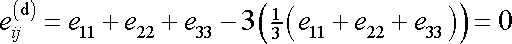 , , |
(2,19) |
je nulový. Relativní objemová změna odpovídající deviátoru
tenzoru malých deformací je nulová. Složky se smíšenými indexy deviátoru
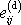 jsou obecně nenulové, složky se shodnými
indexy jsou buď všechny nulové nebo takové, že jejich součet je nulový. Úhly
smyku u deformace popsané takovým tenzorem jsou nenulové, tvar objemových
elementů se deformací mění. Shrneme:
jsou obecně nenulové, složky se shodnými
indexy jsou buď všechny nulové nebo takové, že jejich součet je nulový. Úhly
smyku u deformace popsané takovým tenzorem jsou nenulové, tvar objemových
elementů se deformací mění. Shrneme:
Izotropní část
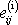 popisuje objemovou deformaci a deviátor
popisuje objemovou deformaci a deviátor
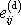 tvarovou deformaci odpovídající tenzoru
malých deformací
tvarovou deformaci odpovídající tenzoru
malých deformací
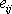 .
.
Obdobně jako tenzor deformace rozložíme i tenzor napětí
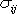 na izotropní část a deviátor;
na izotropní část a deviátor;
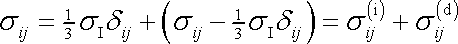 . . |
(2,20) |
Vektor napětí
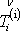 na plošce o normále
na plošce o normále
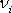 odpovídající izotropní části
odpovídající izotropní části
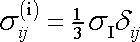 |
(2,21) |
tenzoru napětí je dle (1,82) dán výrazem
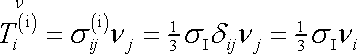 . . |
(2,22) |
Z rovnice
(2,22)
plyne, že pro libovolnou plošku
proloženou daným bodem má vektor napětí
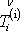 směr normály plošky a na každé plošce
stejnou velikost
směr normály plošky a na každé plošce
stejnou velikost
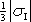 .
Izotropní části
.
Izotropní části
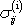 tenzoru napětí
tenzoru napětí
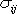 odpovídá čistý tah nebo čistý tlak stejné velikosti
pro všechny orientace plošek procházejících bodem, pro který je tenzor
odpovídá čistý tah nebo čistý tlak stejné velikosti
pro všechny orientace plošek procházejících bodem, pro který je tenzor
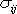 zadán. Je-li
zadán. Je-li
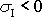 ,
odpovídá popisované napětí známému případu tlaku v kapalině, přičemž
velikost tlaku
,
odpovídá popisované napětí známému případu tlaku v kapalině, přičemž
velikost tlaku
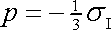 . . |
(2,23) |
Napětí odpovídající deviátoru
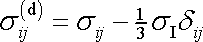 |
(2,24) |
tenzoru napětí
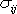 představuje obecné smykové napětí.
představuje obecné smykové napětí.
Zobecněný Hookův zákon pro izotropní látku lze odvodit z předpokladu, že izotropní část tenzoru napětí je úměrná izotropní části tenzoru deformace
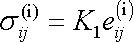 |
(2,25) |
a deviátor tenzoru napětí je úměrný deviátoru tenzoru deformace
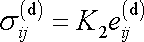 . . |
(2,26) |
Konstanty úměrnosti
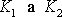 jsou vzájemně různé. Za těchto předpokladů
dostáváme pro tenzor napětí vyjádření
jsou vzájemně různé. Za těchto předpokladů
dostáváme pro tenzor napětí vyjádření
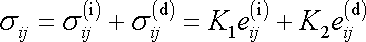 . . |
(2,27) |
Dosadíme-li za
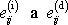 z
(2,16)
a
(2,17)
, máme dále
z
(2,16)
a
(2,17)
, máme dále
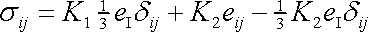 |
neboli
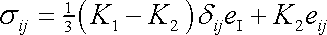 . . |
(2,28) |
Poslední rovnice je až na značení konstant totožná s rovnicí (2,8) , resp. (2,9) , a je tedy zobecněným Hookovým zákonem pro izotropní látku. Porovnáním rovnic dostáváme vztahy mezi konstantami užívanými v rovnicích (2,28) a (2,8)
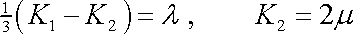 |
(2,29) |
a mezi konstantami z rovnic (2,28) a (2,9)
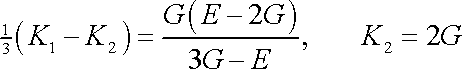 . . |
(2,30) |
Ukázali jsme, že pro izotropní látku získáme z předpokladů (2,25) a (2,26) zobecněný Hookův zákon stejně, jako když užitím prvků symetrie upravujeme rovnici (2,1) .
V minulé stati jsme si ukázali, jak Hookův zákon pro izotropní elastickou látku lze odvodit z předpokladu úměrnosti izotropních částí tenzorů deformace a napětí a úměrnosti jejich deviátorů. Tuto skutečnost lze též interpretovat jako nezávislost objemové a tvarové deformace sledované látky. Rozborem rovnic (2,25) a (2,26) ukážeme nyní podrobněji oprávněnost tohoto tvrzení.
Dosadíme-li do rovnice
(2,25)
vyjádření
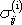 dle
(2,21)
a
dle
(2,21)
a
 dle
(2,16)
, dostáváme po zkrácení
dle
(2,16)
, dostáváme po zkrácení
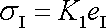 . . |
(2,31) |
Invariant
 pro
pro
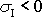 je dle rovnice
(2,23)
roven záporně vzaté
trojnásobné hodnotě tlaku p. Při
je dle rovnice
(2,23)
roven záporně vzaté
trojnásobné hodnotě tlaku p. Při
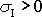 je invariant
je invariant
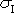 roven trojnásobné hodnotě velikosti vektoru
napětí
(2,22)
, který v tomto případě popisuje ve všech směrech stejný
čistý tah, pro nějž budeme užívat názvu izotropní
tah. Velikost izotropního tahu můžeme, oprostíme-li se od vžité představy,
že písmenem p musí být označen jen
tlak, též označit p. Tlak bude odpovídat hodnotám
p > 0 a izotropní tah hodnotám p
< 0. Rovnici
roven trojnásobné hodnotě velikosti vektoru
napětí
(2,22)
, který v tomto případě popisuje ve všech směrech stejný
čistý tah, pro nějž budeme užívat názvu izotropní
tah. Velikost izotropního tahu můžeme, oprostíme-li se od vžité představy,
že písmenem p musí být označen jen
tlak, též označit p. Tlak bude odpovídat hodnotám
p > 0 a izotropní tah hodnotám p
< 0. Rovnici
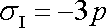 |
(2,32) |
budeme pak pokládat za platnou pro všechny hodnoty
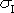 .
.
Invariant
 má dle rovnice
(2,14)
význam relativní změny
objemu
má dle rovnice
(2,14)
význam relativní změny
objemu
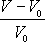 .
Dále budeme pokládat přibližnou rovnici
(2,14)
za přesně splněnou a rovnici
(2,31)
přepíšeme na tvar
.
Dále budeme pokládat přibližnou rovnici
(2,14)
za přesně splněnou a rovnici
(2,31)
přepíšeme na tvar
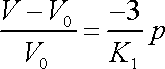 . . |
(2,33) |
Rovnice
(2,33)
má velmi názorný význam;
říká, že relativní změna objemu je úměrná působícímu tlaku, případně
izotropnímu tahu p. Přitom tlaku, tj. hodnotě
p > 0, odpovídá zmenšení
objemu a izotropnímu tahu ( p < 0
) odpovídá zvětšení objemu. Takovýto jednoduchý fyzikální vztah je obsahem
rovnice
(2,25)
. Koeficient úměrnosti
 je roven objemové stlačitelnosti k,
je roven objemové stlačitelnosti k,
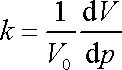 . . |
(2,34) |
Převrácená hodnota objemové stlačitelnosti
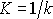 se nazývá modul objemové pružnosti. Mezi ním a konstantou
se nazývá modul objemové pružnosti. Mezi ním a konstantou
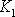 z rovnice
(2,25)
platí vztah
z rovnice
(2,25)
platí vztah
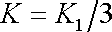 . . |
(2,35) |
O jeho platnosti se lze přesvědčit, vypočteme-li dle definiční rovnice (2,34) objemovou stlačitelnost k příslušnou rovnici (2,33) a nalezneme její převrácenou hodnotu. Zavedeme-li do rovnice (2,33) modul objemové pružnosti K, můžeme ji přepsat na tvar
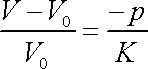 , , |
(2,36) |
který jasně ukazuje závislost relativní změny objemu na všestranném napětí či tlaku p.
Abychom objasnili význam rovnice (2,26) , obrátíme pozornost na deformaci vyjádřenou tenzorem
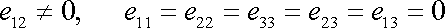 . . |
(2,37) |
Jak jsme ukázali na konci článku 1.2, vyjadřuje takový tenzor smyk o úhel
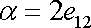 |
(2,38) |
v rovině kolmé k třetí souřadnicové ose. Jeho
první invariant
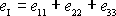 je zřejmě nulový. Proto je nulová celá
izotropní část tenzoru
(2,37)
a tenzor je shodný se svým deviátorem
je zřejmě nulový. Proto je nulová celá
izotropní část tenzoru
(2,37)
a tenzor je shodný se svým deviátorem
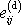 ;
;
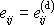 .
Tenzorová rovnice
(2,26)
pro tenzor
(2,37)
se redukuje na jedinou složkovou
rovnici
.
Tenzorová rovnice
(2,26)
pro tenzor
(2,37)
se redukuje na jedinou složkovou
rovnici
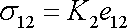 , , |
(2,39) |
která ukazuje, že smykové napětí
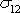 je úměrné smykové deformaci
je úměrné smykové deformaci
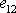 .
To je stejný vztah, jaký bývá uváděn (např. [6] ) v tvaru
.
To je stejný vztah, jaký bývá uváděn (např. [6] ) v tvaru
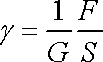 . . |
(2,40) |
V rovnici
(2,40)
je úhel smyku a značen
g a G
je modul pružnosti ve smyku. Smykové napětí je vyjádřeno poměrem smykově
působící síly F k velikosti S plochy, na kterou tato síla působí. Smykové
napětí
 je v souřadnicové soustavě, v níž
uvažujeme tenzor
(2,37)
(v této soustavě má síla F směr první souřadnicové osy) vyjádřeno
složkou
je v souřadnicové soustavě, v níž
uvažujeme tenzor
(2,37)
(v této soustavě má síla F směr první souřadnicové osy) vyjádřeno
složkou
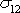 tenzoru napětí. Rovnici
(2,40)
můžeme tedy
přepsat na tvar
tenzoru napětí. Rovnici
(2,40)
můžeme tedy
přepsat na tvar
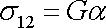 |
a užijeme-li vztahu (2,38) , dostáváme dále
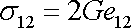 . . |
(2,40´) |
Porovnáme-li poslední rovnici s rovnicí (2,39) , dostáváme vztah
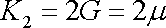 |
(2,41) |
mezi konstantou
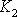 a modulem pružnosti ve smyku G,
který, jak jsme již uvedli (text před rovnicí
(2,8)
), je totožný
s Laméovým koeficientem m.
a modulem pružnosti ve smyku G,
který, jak jsme již uvedli (text před rovnicí
(2,8)
), je totožný
s Laméovým koeficientem m.
Právě provedeným rozborem jsme ukázali, že pro deformaci popsanou tenzorem (2,37) rovnice (2,26) je až na užité značení totožná s elementárním Hookovým zákonem pro smyk. Pro obecnou deformaci rovnice (2,26) udává, že poměr složek se stejnými indexy deviátoru napětí a deviátoru deformace je stejný jako poměr smykového napětí ke smykové deformaci daný Hookovým zákonem pro smyk (2,40) , resp. (2,40´) .
V rovnici
(2,26)
nahradíme víceindexové značení složek
označením, v kterém libovolnou složku deviátoru napětí označíme
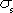 a jí odpovídající složku deviátoru
deformace
a jí odpovídající složku deviátoru
deformace
 .
Dále v téže rovnici nahradíme dle
(2,41)
koeficient
.
Dále v téže rovnici nahradíme dle
(2,41)
koeficient
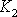 dvojnásobnou hodnotou modulu smyku 2G.
Dostaneme tak rovnici
dvojnásobnou hodnotou modulu smyku 2G.
Dostaneme tak rovnici
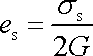 , , |
(2,42) |
která charakterizuje chování lineárně elastické látky při
tvarové deformaci. Charakteristiku doplníme rovnicí
(2,36)
popisující chování
látky při objemové deformaci. Relativní objemovou změnu
 ,
která pro uvažované malé deformace je ve velmi dobrém přiblížení rovna
invariantu
,
která pro uvažované malé deformace je ve velmi dobrém přiblížení rovna
invariantu
 ,
označíme
,
označíme
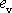 a budeme ji nazývat objemová deformace. Se
symbolem
a budeme ji nazývat objemová deformace. Se
symbolem
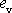 má rovnice
(2,36)
tvar
má rovnice
(2,36)
tvar
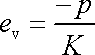 . . |
(2,43) |
Izotropní lineárně elastická látka, které v reologické klasifikaci říkáme hookovská látka nebo též klasická elastická látka, je charakterizována rovnicemi (2,42) a (2,43) , které udávají, že tvarová i objemová deformace jsou přímo úměrné působícímu napětí.
Vlastnosti jednotlivých hookovských látek se liší velikostí
dvou materiálových konstant, kterými v rovnicích
(2,42)
a
(2,43)
jsou
modul pružnosti ve smyku G
a modul objemové pružnosti K. Kromě konstant G a K
lze chování hookovské látky vystihnout i jinou dvojicí materiálových
konstant, např. Laméovými koeficienty l a m, moduly
E a G, konstantami
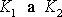 z rovnic
(2,24)
a
(2,25)
. Některé
vztahy mezi uvedenými konstantami jsou dány rovnicemi
(2,29)
,
(2,30)
,
(2,35)
,
(2,41)
. Porovnáním rovnic
(2,8)
a
(2,9)
dostáváme vztah mezi koeficientem l a moduly
E a G:
z rovnic
(2,24)
a
(2,25)
. Některé
vztahy mezi uvedenými konstantami jsou dány rovnicemi
(2,29)
,
(2,30)
,
(2,35)
,
(2,41)
. Porovnáním rovnic
(2,8)
a
(2,9)
dostáváme vztah mezi koeficientem l a moduly
E a G:
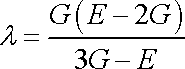 . . |
(2,44) |
Dosadíme-li do první z rovnic
(2,29)
za
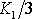 dle
(2,35)
modul objemové pružnosti K,
dostaneme vztah mezi koeficientem l a moduly
K a G = m ;
dle
(2,35)
modul objemové pružnosti K,
dostaneme vztah mezi koeficientem l a moduly
K a G = m ;
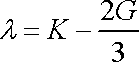 . . |
(2,45) |
Zdůvodnění vztahu (2,44) užitím definice Youngova modulu E a některé vztahy mezi dalšími materiálovými konstantami hookovské látky uvedeme v kap. 3. Podrobná tabulka přepočtů různých materiálových konstant hookovské látky, z nichž vždy dvě jsou nezávisle volitelné, je uvedena např. v [1], str. 178.
Nezávislost objemové a tvarové deformace je zachována i pro
reologicky složitější látky, než je hookovská látka. Reologické chování různých
látek se však výrazněji liší v tvarové než v objemové deformaci.
Např. tvarová deformace tuhého tělesa je nulová a ideální kapalina neklade
tvarové deformaci žádný odpor. Tyto rozdíly lze vystihnout tvrzením, že modul
pružnosti ve smyku pro tuhé těleso
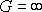 a pro ideální kapalinu G
= 0. Přitom jak pro tuhé těleso, tak i pro ideální kapalinu předpokládáme
nestlačitelnost (rozumí se objemovou nestlačitelnost). Tedy v objemové
deformovatelnosti se oba modely - v reologické terminologii obě látky -
neliší. Oba zmíněné krajní modely se obvykle do reologické klasifikace
nezařazují, ale i když porovnáme hookovskou látku a viskózní kapalinu -
newtonovskou látku - , které již v reologické klasifikaci vystupují, liší
se tyto modely daleko více v tvarové než v objemové deformaci. Proto
se při běžné reologické klasifikaci látek omezujeme na porovnávání jejich
vlastností při tvarové deformaci. Porovnání vlastností při objemové deformaci
se provádí jen při některých podrobnějších reologických studiích.
a pro ideální kapalinu G
= 0. Přitom jak pro tuhé těleso, tak i pro ideální kapalinu předpokládáme
nestlačitelnost (rozumí se objemovou nestlačitelnost). Tedy v objemové
deformovatelnosti se oba modely - v reologické terminologii obě látky -
neliší. Oba zmíněné krajní modely se obvykle do reologické klasifikace
nezařazují, ale i když porovnáme hookovskou látku a viskózní kapalinu -
newtonovskou látku - , které již v reologické klasifikaci vystupují, liší
se tyto modely daleko více v tvarové než v objemové deformaci. Proto
se při běžné reologické klasifikaci látek omezujeme na porovnávání jejich
vlastností při tvarové deformaci. Porovnání vlastností při objemové deformaci
se provádí jen při některých podrobnějších reologických studiích.
Tvarová deformace se nejběžněji vyjádří jako smyková
deformace. Pro smykové napětí se užívá označení t. Smyková deformace se
vyjadřuje úhlem smyku, který pro smyk popsaný tenzorem
(2,37)
je roven
 a kterému je normou přiděleno označení g namísto v rovnici
(2,38)
užitého
označení a.
S právě zavedeným označením a s vědomím toho, že pro základní
reologickou klasifikaci užíváme tvarovou deformaci, budeme hookovskou látku
reologicky charakterizovat takto:
a kterému je normou přiděleno označení g namísto v rovnici
(2,38)
užitého
označení a.
S právě zavedeným označením a s vědomím toho, že pro základní
reologickou klasifikaci užíváme tvarovou deformaci, budeme hookovskou látku
reologicky charakterizovat takto:
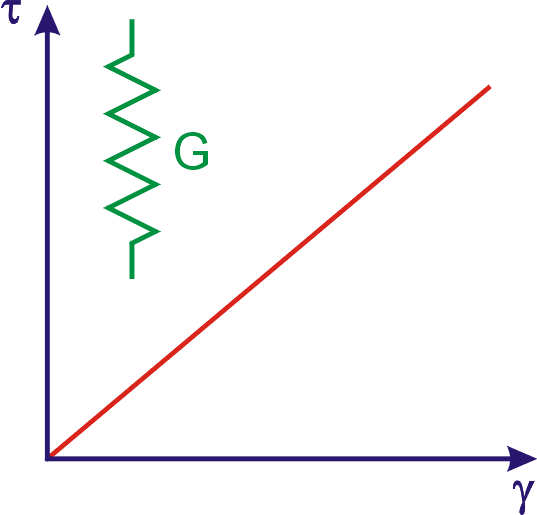
Hookovská neboli klasická elastická látka je látka, pro kterou napětí je přímo úměrné deformaci. Tuto závislost vyjádříme charakteristickou reologickou rovnicí
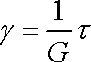 , , |
(2,46) |
graficky ji vyjádříme přímou úměrností a jako model pro tuto závislost zvolíme pružinu s připsanou hodnotou modulu pružnosti ve smyku G vystihující tuhost pružiny (viz obr.22).
 V článcích
2.2, 2.3 a 2.4 budeme postupně charakterizovat izotropní viskózní,
visko-elastické a plastické látky. Klasifikaci opět provedeme dle tvarové
deformace a pro látky napíšeme charakteristické reologické rovnice, které
popíší rozličnou závislost úhlu smyku g na smykovém
napětí t v těchto látkách.
V článcích
2.2, 2.3 a 2.4 budeme postupně charakterizovat izotropní viskózní,
visko-elastické a plastické látky. Klasifikaci opět provedeme dle tvarové
deformace a pro látky napíšeme charakteristické reologické rovnice, které
popíší rozličnou závislost úhlu smyku g na smykovém
napětí t v těchto látkách.
Výše popsaná reologická charakteristika látek je omezena na případ malých deformací či malých rychlostí deformace neboli na tzv. lineární případ. Další reologicky zajímavé chování látek nastává, když se překročí meze linearity. V následující stati probereme odchylky od linearity pro elastické látky.
 Vyšetřujeme-li
experimentálně vztah mezi napětím a deformací pro nějakou konkrétní látku,
přímá úměrnost mezi napětím a deformací bývá v dobrém přiblížení splněna
jen v určitém omezeném, pro různé látky různě velkém, intervalu napětí.
Vyšetřujeme-li
experimentálně vztah mezi napětím a deformací pro nějakou konkrétní látku,
přímá úměrnost mezi napětím a deformací bývá v dobrém přiblížení splněna
jen v určitém omezeném, pro různé látky různě velkém, intervalu napětí.
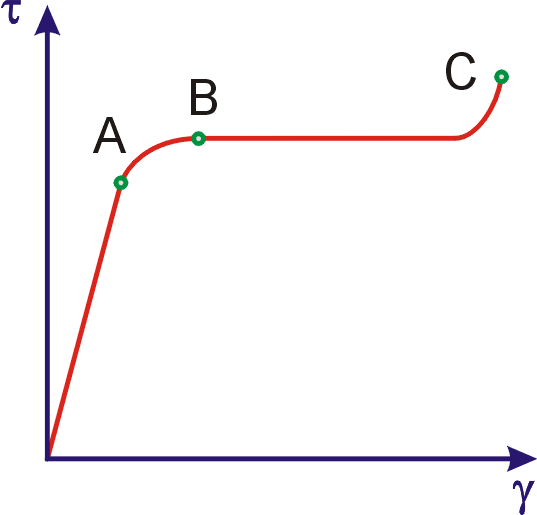
Pro některé kovové materiály je závislost napětí na
deformaci popsána křivkou schematicky znázorněnou na obr.23. Až po napětí
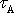 odpovídající bodu A křivky je deformace
úměrná napětí. Bodu A říkáme mez úměrnosti. Pro napětí
odpovídající bodu A křivky je deformace
úměrná napětí. Bodu A říkáme mez úměrnosti. Pro napětí
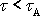 se materiál chová jako hookovská látka.
Překročí-li napětí hodnotu
se materiál chová jako hookovská látka.
Překročí-li napětí hodnotu
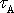 ,
přímá úměrnost mezi napětím a deformací je porušena. Až po napětí
,
přímá úměrnost mezi napětím a deformací je porušena. Až po napětí
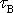 ,
které odpovídá bodu B křivky, deformace vzorku po odstranění napětí klesá na
nulovou hodnotu. Vzorek po odtížení zaujímá svůj původní tvar.
,
které odpovídá bodu B křivky, deformace vzorku po odstranění napětí klesá na
nulovou hodnotu. Vzorek po odtížení zaujímá svůj původní tvar.
Látce, která po odstranění vnějšího silového působení zaujímá svůj původní tvar, říkáme pružná neboli elastická.
Bod B z obr.23 nazýváme mezí pružnosti nebo též mezí elasticity. Při dalším zvyšování napětí vzorek po odtížení zůstane již trvale deformován. Velikost trvalé deformace nezávisí jen na velikosti působící síly, ale i na době jejího působení. Po překročení meze pružnosti začne materiál plasticky téct, což znamená, že jeho deformace závisí nejen na velikosti napětí, ale i na časovém a prostorovém průběhu napětí i deformace. Graf z obr.23 mezi bodem B a C, kdy se vzorek přetrhne, tedy nepopisuje plně chování látky. Nejjednodušší formu plastického tečení popíšeme a o obecné teorii plasticity se zmíníme v čl. 2.4. Jaké mechanizmy vedou k přetržení vzorku a kdy přetržení nastane, je také předmětem reologických úvah. Těmito otázkami se zabývá teorie pevnosti látek, kterou spolu s její modernější částí - lomovou mechanikou - probereme v čl. 2.6.
V oblasti mezi body A a B grafu z obr.23 je látka
elastická, po odtížení zaujme svůj původní tvar, ale není hookovská, deformace
není lineární funkcí napětí. Říkáme, že látka je v uvedené oblasti
nelineárně elastická. Látka z grafu na obr.23 je nelineárně elastická pro
napětí t z intervalu
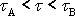 .
Je to poměrně malý a ne příliš významný obor jejího reologického chování.
.
Je to poměrně malý a ne příliš významný obor jejího reologického chování.
 Pro řadu látek však
lineární vztah mezi napětím a deformací není splněn ani pro velmi malá napětí.
Tvar závislosti je např. dán grafem znázorněným na obr.24. Užití Hookova zákona
pro látku z obr.24 má i pro nejmenší napětí pouze ráz první aproximace.
Přerušovaná čára na grafu odpovídá závislosti, kterou získáme, když za
konstantu úměrnosti napětí a deformace v Hookově zákoně vezmeme limitní
hodnotu poměru
Pro řadu látek však
lineární vztah mezi napětím a deformací není splněn ani pro velmi malá napětí.
Tvar závislosti je např. dán grafem znázorněným na obr.24. Užití Hookova zákona
pro látku z obr.24 má i pro nejmenší napětí pouze ráz první aproximace.
Přerušovaná čára na grafu odpovídá závislosti, kterou získáme, když za
konstantu úměrnosti napětí a deformace v Hookově zákoně vezmeme limitní
hodnotu poměru
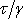 pro
pro
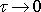 .
Touto závislostí obvykle aproximujeme chování látky, pokládáme-li ji za
hookovskou. Vidíme, že je to hrubá aproximace a že přesnější popis deformačního
chování látky lze podat pouze, uvážíme-li její nelineárně elastický charakter.
.
Touto závislostí obvykle aproximujeme chování látky, pokládáme-li ji za
hookovskou. Vidíme, že je to hrubá aproximace a že přesnější popis deformačního
chování látky lze podat pouze, uvážíme-li její nelineárně elastický charakter.
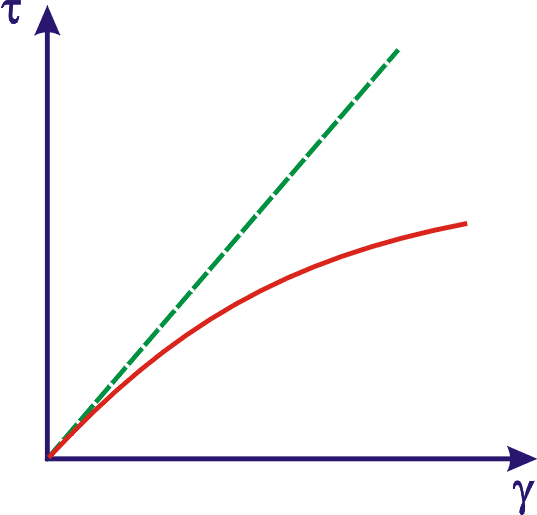 Závislost deformace na
napětí typu znázorněného na obr.24 mají některé kovové materiály, např. měď.
Ještě typičtějšími nelineárně elastickými materiály jsou vulkanizované kaučuky
(pryže). Vulkanizovaný přírodní kaučuk může dosáhnout deformace, při níž se
délka vzorku zvětší více než sedminásobně a přitom po odstranění deformující
síly zaujme vzorek svůj původní tvar. Deformace je tedy elastická, není však lineární.
Typická závislost napětí na deformaci pro pryž z přírodního kaučuku
(vulkanizovaný přírodní kaučuk) je znázorněna na obr.25. Deformace je na grafu
označena
Závislost deformace na
napětí typu znázorněného na obr.24 mají některé kovové materiály, např. měď.
Ještě typičtějšími nelineárně elastickými materiály jsou vulkanizované kaučuky
(pryže). Vulkanizovaný přírodní kaučuk může dosáhnout deformace, při níž se
délka vzorku zvětší více než sedminásobně a přitom po odstranění deformující
síly zaujme vzorek svůj původní tvar. Deformace je tedy elastická, není však lineární.
Typická závislost napětí na deformaci pro pryž z přírodního kaučuku
(vulkanizovaný přírodní kaučuk) je znázorněna na obr.25. Deformace je na grafu
označena
 ,
abychom zdůraznili, že se jedná o velkou deformaci, kterou je nutno vyjádřit
tenzorem velkých deformací
(1,24)
. Při velkých deformacích je podstatné
rozlišení mezi silou působící na vzorek a napětím, při jehož výpočtu musíme
uvažovat skutečnou plochu průřezu vzorku při dané deformaci. Pryže lze pokládat
za objemově nestlačitelné materiály. Potom např. při sedmi-násobném protažení
vzorku plocha jeho příčného průřezu se zmenší na sedminu původní plochy. Tuto
změnu plochy průřezu zřejmě nelze zanedbat.
,
abychom zdůraznili, že se jedná o velkou deformaci, kterou je nutno vyjádřit
tenzorem velkých deformací
(1,24)
. Při velkých deformacích je podstatné
rozlišení mezi silou působící na vzorek a napětím, při jehož výpočtu musíme
uvažovat skutečnou plochu průřezu vzorku při dané deformaci. Pryže lze pokládat
za objemově nestlačitelné materiály. Potom např. při sedmi-násobném protažení
vzorku plocha jeho příčného průřezu se zmenší na sedminu původní plochy. Tuto
změnu plochy průřezu zřejmě nelze zanedbat.
V souvislosti se zkoumáním elastických vlastností pryží (gum) byla rozvinuta nelineární teorie elasticity, která se též nazývá teorií velkých deformací. Tato teorie musí k popisu deformace užívat některý z tenzorů velkých deformací, např. tenzor (1,28) . Podmínky rovnováhy uvažuje v deformovaném stavu vzorku a nepřevádí veškeré výpočty k nedeformovanému vzorku, jako se to provádí v teorii pružnosti hookovské látky (srov. kap. 3). Teorie velkých deformací vztah mezi deformací a napětím neřeší úpravou Hookova zákona, ale vychází z potenciální energie, kterou vzorek získá deformací. Tato energie se nazývá elastický potenciál nebo též hustota energie deformace. Znalost závislosti elastického potenciálu na parametrech deformace, např. na invariantech tenzoru velkých deformací, vystihuje elastické chování látky při velkých deformacích a nahrazuje tak znalost dvou elastických konstant vystihujících elastické chování hookovské látky. I když teorie velkých deformací je složitou teorií, je dovedena do tvaru, který nejen umožňuje najít elastickou charakteristiku nelineárně elastické látky, ale dává i možnost určit rozložení napětí a deformací při některých konkrétních druzích namáhání nelineárně elastických vzorků (viz např. [20], [21], [33] ).