Již v článcích 7.1.4 a 7.2.1 byla uvedena některá fakta o elektrických dipólových momentech atomů a molekul. Zejména bylo uvedeno, že volný atom v nulovém elektrickém poli má vždy nulový elektrický dipólový moment, zatímco molekuly existují jak polární s nenulovým vlastním momentem, tak nepolární s nulovým vlastním momentem. Vnější elektrické pole může i v nepolární látce indukovat elektrické momenty atomů či molekul, díky elektronové a iontové (atomové) polarizovatelnosti těchto objektů.
Obvykle se předpokládá, že jednotlivé atomy, i nepolární molekuly jako celek, se chovají kvazielasticky. Indukované elektrické momenty jsou pak úměrné intenzitě lokálního pole E 1 na atom či molekulu působícího. Jejich střední hodnoty ve směru pole lze vyjádřit vztahy
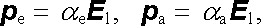 |
(7.47) |
v nichž α e a α a jsou tzv. činitelé elektronové a atomové polarizovatelnosti, p e, p a značí časové střední hodnoty příslušných momentů. Pro celkový moment molekuly p lze tedy psát
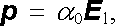 |
(7.48) |
přičemž α 0 = α e + α a je její celkový činitel polarizovatelnosti.
Na základě právě uvedených úvah jsme vytvořili model chování nepolární molekuly ve vnějším elektrostatickém poli. Chování každé molekuly je popsáno hodnotou jejího činitele polarizovatelnosti. Je zřejmé, že ze znalosti těchto činitelů je obecně možné vypočítat elektrickou susceptibilitu (resp. permitivitu) dané látky. Předpokládáme-li, že v dostatečně malém objemu V je přítomno nV molekul, jejichž polarizovatelnosti a elektrické momenty v lokálním elektrostatickém poli E1 označíme α i a pi, můžeme podle definice (1.161) pro velikost polarizace P psát
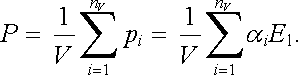 |
(7.49) |
Ve speciálním případě, kdy budou polarizovatelnosti všech molekul stejné a rovné α 0 , dostaneme výsledek
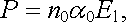 |
(7.50) |
v němž jsme zavedli n0 = nV /V jako koncentraci molekul v jednotce objemu.
Elektrostatické pole E1 působící na molekuly není ovšem obecně totožné s makroskopickým polem E přítomným uvnitř dané látky. Pouze v případě plynů, kdy je počet molekul v jednotkovém objemu velmi malý, můžeme zanedbat interakce mezi nimi a obě pole ztotožnit; E1 = E. Pro elektrickou susceptibilitu plynů χ e pak podle definiční relace (1.255) dostaneme
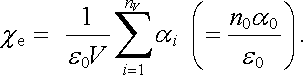 |
(7.51) |
Podobně permitivitu ε vyjádříme ve tvaru
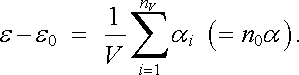 |
(7.52) |
V případě kapalin a pevných látek je situace složitější. Pro výpočet susceptibility je nutné určit lokální pole E 1 působící na molekuly uvnitř látky. Toto pole má charakter časové střední hodnoty mikroskopického pole (srov. oddíl 5.4). Pro jeho výpočet navrhl H. A. Lorentz postup umožňující určit vztah tohoto pole k makroskopickému poli E uvnitř dielektrika. Kolem vyšetřované molekuly vymezíme v dielektriku malou kulovou oblast. Její poloměr zvolíme dostatečně velký, abychom dielektrikum vně této koule mohli považovat za kontinuum a použít pro jeho popis pojmu permitivity. Lokální pole E 1 působící na vybranou molekulu bude potom možné vyjádřit jako součet makroskopického pole uvnitř zvolené dutiny E d a pole E ℜ' , které v místě vybrané molekuly budí molekuly nacházející se uvnitř zvolené koule. Tedy
 |
(7.53) |
Pole E ℜ' představuje časovou střední hodnotu mikroskopického pole vzbuzeného v místě vybrané molekuly jejími nejbližšími sousedy. Musí být proto, obecně řečeno, počítáno mikroskopicky. V některých případech však můžeme soudit na jeho nulovou hodnotu. Takovou situaci lze očekávat především v kapalinách a v amorfních pevných látkách, které jsou izotropní a u nichž jsou molekuly rozmístěny zcela nepravidelně, takže lze očekávat vyrušení jejich jednotlivých příspěvků. Podobné poměry nastávají v řadě krystalických látek s vy-sokou (především kubickou) symetrií. Také v těchto látkách dochází k vyrušení příspěvků jednotlivých molekul a platí E ℜ' = 0 . V uvedených případech dostaneme místo (7.53) jednodušší vztah E 1 = E d, čímž se výpočet permitivity značně zjednodušší.
Nadále se budeme zabývat jen těmi látkami, u nichž je uvedené zjednodušení možné. Potom lze použít výsledek (1.287) a pole v dutině E d vyjádřit pomocí makroskopického pole E uvnitř dielektrika.
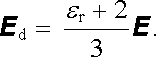 |
Odtud, vezmeme-li v úvahu vztah
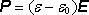 , dostaneme
po dosazení do
(7.49)
, dostaneme
po dosazení do
(7.49)
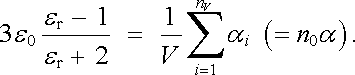 |
(7.54) |
Rovnice vyjadřuje vzájemný vztah relativní permitivity nepolárních látek a polarizovatelnosti jejich molekul za předpokladu, že je možné zanedbat "mikroskopickou" složku E ℜ' lokálního pole E d. Užitím Avogadrova zákona ji lze přepsat do obvyklého tvaru
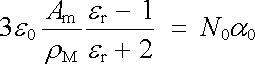 , , |
(7.54a) |
nazývaného Clausiův-Mosottiův vztah. Veličina Am v něm značí poměrnou molekulovou hmotnost dané látky, ρ M její hustotu a N0 Avogadrovu konstantu.
Clausiova-Mosottiova formule je v principu použitelná pro všechny nepolární kapaliny a plyny s tím přiblížením, s jakým je možné zanedbat "mikroskopickou" složku E ℜ' lokálního pole. Z jejího tvaru vyplývá, že teplotní závislost permitivity nepolárních látek je dána jen teplotní závislostí počtu molekul N0 v jednotce objemu. Tato veličina však nemůže v kapalinách a pevných látkách jevit výraznou teplotní závislost. Permitivitu nepolárních látek můžeme tedy považovat za teplotně nezávislou.
Pomocí Clausiovy-Mosottiovy formule je možné vypočítat permitivitu látky, jestliže je znám počet molekul v jednotce objemu a jejich polarizovatelnost. Je však také možný obrácený postup. Ze změřené hodnoty permitivity umožňuje Clausiova-Mosottiova formule vypočítat polarizovatelnost molekul. Z chování permitivity v časově proměnných polích je dále možné odlišit elektronovou polarizovatelnost od polarizovatelnosti atomové. Experimentální studium permitivity umožňuje tudíž určovat jisté mikrofyzikální parametry dané látky, z nichž je dále možné usuzovat na strukturu jejich molekul. Studiem otázek podobného druhu se zabývá fyzika dielektrik a fyzikální chemie.
V článku 6.2.2 jsme ukázali, že magnetický moment vložený do vnějšího magnetického pole koná Larmorovu precesi s Larmorovou frekvencí ω L = γ B . Aplikujeme-li tento výsledek na pohyb elektronu v atomu, přijdeme k závěru, že magnetické pole ovlivní pohyb elektronu způsobem, který je ekvivalentní vzniku jistého antiparalelního magnetického momentu.
Hodnotu tohoto momentu vypočteme pomocí
jednoduchého modelu využívajícího výsledků příkladu 3.4.6a. Elektron nechť
koná rovnoměrný pohyb po kruhové dráze, jejíž rovina svírá jistý úhel ϑ
s osou z, do jejíhož směru
orientujeme vnější pole B
.
Larmorova precese změní střední hodnotu momentu hybnosti elektronu o hodnotu
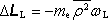 , kde
, kde
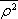 je střední kvadratický poloměr průmětu dráhy
do roviny kolmé ke směru pole. Pro indukovaný magnetický moment m
d pak dostaneme podle
(3.128)
je střední kvadratický poloměr průmětu dráhy
do roviny kolmé ke směru pole. Pro indukovaný magnetický moment m
d pak dostaneme podle
(3.128)
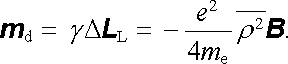 |
(7.55) |
Uvažujme nyní model atomu obsahujícího Z elektronů. Předpokládejme, že všechny elektrony obíhají po kruhových drahách o poloměrech r1, r2,..., rZ. Tyto dráhy nechť jsou rovnoměrně prostorově rozložené tak, aby prostorové rozložení elektronového náboje mělo kulovou symetrii. Celkový magnetický moment indukovaný vnějším polem bude dán součtem momentů jednotlivých elektronů. Tedy
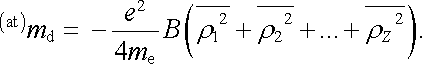 |
(7.56) |
Zavedeme-li střední kvadratickou hodnotu
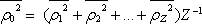 můžeme vzorec zapsat v jednodušším tvaru
můžeme vzorec zapsat v jednodušším tvaru
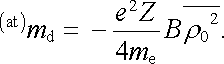 |
(7.57) |
Pro
kulově symetrický atom však můžeme veličinu
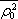 snadno vyjádřit pomocí střední kvadratické hodnoty
poloměru dráhy
snadno vyjádřit pomocí střední kvadratické hodnoty
poloměru dráhy
 , která má názornější význam.
Ztotožníme-li počátek soustavy souřadné s jádrem atomu a orientujeme-li osu z ve směru pole, bude pro střední
hodnoty čtverců sou-řadnic elektronů
, která má názornější význam.
Ztotožníme-li počátek soustavy souřadné s jádrem atomu a orientujeme-li osu z ve směru pole, bude pro střední
hodnoty čtverců sou-řadnic elektronů
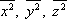 platit
platit
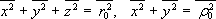 .
Avšak vzhledem ke kulové symetrii atomu platí
.
Avšak vzhledem ke kulové symetrii atomu platí
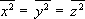 ,
takže
,
takže
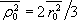 .
Indukovaný magnetický moment atomu tedy můžeme vyjádřit ve tvaru
.
Indukovaný magnetický moment atomu tedy můžeme vyjádřit ve tvaru
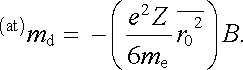 |
(7.58) |
Obsahuje-li uvažovaná látka n0 stejných atomů v jednotce objemu, je celkový moment indukovaný v jednotce objemu vnějším polem B roven n0-násobku momentu (7.58) . Pro diamagnetickou susceptibilitu dostaneme pak podle její definice (3.140)
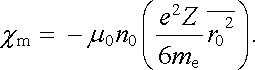 |
(7.59) |
Pro experimentální ověření platnosti Langevinova vztahu (7.59) je výhodné vyjádřit počet atomů v jednotce objemu n0 užitím Avogadrova zákona pomocí molekulové hmotnosti Am hustoty ρ M a Avogadrovy konstanty N0; n0 = ρ M N0/Am. Pro susceptibilitu pak dostaneme
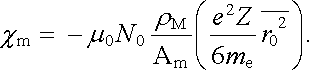 |
(7.60) |
Problémem zůstává určení veličiny
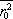 .
Vezmeme-li za ni řádovou hodnotu poloměru atomu (10-10 m), dostaneme
po dosazení hodnot univerzálních konstant χ
m ~ (
ρ
M
N0/Am).10-8. Vidíme tedy, že z Langevinova vzorce
pro diamagnetika vychází teplotně nezávislá susceptibilita, jejíž řádová
hodnota souhlasí s experimentem (srov. tabulku v článku 7.2.2).
.
Vezmeme-li za ni řádovou hodnotu poloměru atomu (10-10 m), dostaneme
po dosazení hodnot univerzálních konstant χ
m ~ (
ρ
M
N0/Am).10-8. Vidíme tedy, že z Langevinova vzorce
pro diamagnetika vychází teplotně nezávislá susceptibilita, jejíž řádová
hodnota souhlasí s experimentem (srov. tabulku v článku 7.2.2).
J. H. van Vleck vypracoval ve dvacátých
letech kvantovou teorii diamagnetismu atomů a molekul. Pro diamagnetickou
susceptibilitu získal výraz, jehož jeden člen je totožný s Langevinovým vztahem
(7.59)
. Hodnotu veličiny
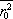 je v něm ovšem třeba počítat užitím
aparátu kvantové mechaniky.[71]
je v něm ovšem třeba počítat užitím
aparátu kvantové mechaniky.[71]
První kvantitativní teorii paramagnetismu nekovů vypracoval na počátku našeho století rovněž P. Langevin. Jeho teorie vychází z dnes již plně ověřeného předpokladu, že atomy, respektive molekuly paramagnetických látek mají vlastní magnetické momenty, které se účinkem vnějšího magnetického pole částečně orientují a vytvářejí makroskopickou magnetizaci. P. Debye ukázal později (r. 1912), že se stejný mechanismus může podílet rovněž na dielektrické polarizaci některých polárních látek, a použil Langevinovu teorii k výpočtu jejich permitivity. V tomto článku si postupně všimneme obou problémů.
a) Magnetická susceptibilita paramagnetik
Langevinova teorie vychází z předpokladu, že každý atom (respektive molekula) paramagnetické látky má vlastní magnetický moment m , jehož velikost nezávisí v prvním přiblížení na velikosti vnějšího magnetického pole. Dále předpokládá, že jednotlivé molekuly na sebe vzájemně nepůsobí, takže orientace dané molekuly není závislá na orientaci jiných molekul. Nepůsobí-li vnější pole, jsou magnetické momenty jednotlivých molekul orientovány chaoticky, takže výsledný magnetický moment makroskopické části látky je nulový. Ve vnějším poli jsou však jednotlivé momenty podrobeny silovému působení (viz čl. 3.4.2), takže může dojít k jejich částečnému uspořádání do směru pole.
Předpokládejme, že v malém objemu látky V je obsaženo nV
molekul, jejichž magnetické momenty m
1, m
2, ...,
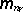 svírají se směrem vnějšího pole úhly ϑ
1
,
ϑ
2,...,
svírají se směrem vnějšího pole úhly ϑ
1
,
ϑ
2,...,
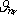 .
Magnetizace látky M bude podle čl.
3.5.2 rovna výsledné složce magnetického momentu do směru pole (výsledné složky
v jiných směrech jsou ovšem nulové)
.
Magnetizace látky M bude podle čl.
3.5.2 rovna výsledné složce magnetického momentu do směru pole (výsledné složky
v jiných směrech jsou ovšem nulové)
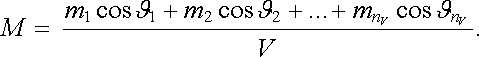 |
(7.61) |
Ve speciálním případě, kdy jsou všechny molekuly stejného druhu, mají všechny momenty stejnou velikost. Tedy
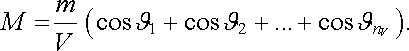 |
(7.62) |
Zavedeme-li
střední hodnotu
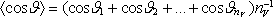 a kon-centraci molekul n0 = nV/V,
dostaneme
a kon-centraci molekul n0 = nV/V,
dostaneme
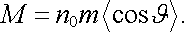 |
(7.63) |
Problémem nyní zůstává výpočet střední hodnoty ℘ ϒ cosϑ ℘ ± , pro nějž je nutné použít statistické metody (srov. metody používané v kinetické teorii plynů; viz např. [10]). Pravděpodobnost určité hodnoty cosϑ je určena potenciální energií daného dipólu v magnetickém poli B působícím na dipól, pro níž podle (3.107) platí Wm = - m .B = - mB cosϑ . (Díky tomu, že susceptibilita paramagnetik je velmi malá, můžeme pole B působící na atomové magnetické momenty vždy s dostatečnou přesností považovat za totožné s vnějším makroskopickým polem.) Funkce cosϑ má charakter spojité náhodné veličiny charakterizované hustotou pravděpodobnosti p(cosϑ ), pro niž platí
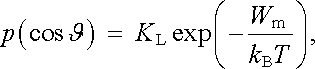 |
kde KL je normovací konstanta. Použítím obecného výrazu pro výpočet střední hodnoty náhodné veličiny s normovanou hustotou pravděpodobnosti p(cosϑ ) dostaneme po přechodu k nové integrační proměnné ϑ výraz
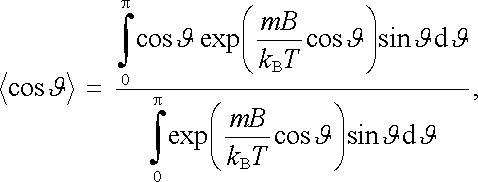 |
po jehož integraci získáme výsledek
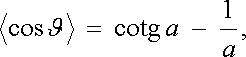 |
(7.64) |
v němž jsme označili a = mB/kBT = μ 0 mH/kBT . Veličinu (7.64) je zvykem označovat symbolem L(a) a nazývat Langevinovou funkcí
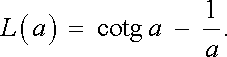 |
(7.65) |
Jejím využitím lze vyjádřit magnetizaci M vztahem
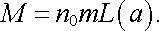 |
(7.66) |
Jak vidíme, je magnetizace paramagnetika obecně dosti složitou funkcí teploty a magnetického pole. S výjimkou oboru velmi nízkých teplot a vysokých polí vždy platí a = μ 0 mH/kBT << 1. Pro tento případ můžeme Langevinovu funkci aproximovat jejím rozvojem v mocninnou řadu. Platí
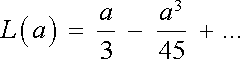 |
Ponecháme-li v tomto rozvoji jen první člen, dostaneme z (7.66) pro susceptibilitu χ m = M/H
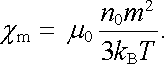 |
(7.67) |
Tento výraz má již tvar Curieova zákona (3.144) . Oba výrazy se ztotožní, položíme-li pro Curieovu konstantu
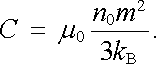 |
(7.68) |
Langevinova teorie tedy dává kvalitativně správnou teplotní závislost paramagnetické susceptibility. Srovnáním naměřené teplotní závislosti susceptibility můžeme určit hodnotu Curieovy konstanty a z ní je podle (7.68) možné vypočítat velikost magnetického momentu molekul m. Pro další fyzikální interpretaci takto získané veličiny je však již nutné vzít v úvahu zákonitosti kvantové mechaniky.
L. Brillouin modifikoval Langevinovu teorii tak, aby vyhovovala omezením, která kvantová mechanika klade na prostorovou orientaci atomových a molekulárních magnetických momentů. Místo (7.66) získal obecnější vzorec, který lépe popisuje skutečnou situaci. Obecná kvantová teorie paramagnetismu atomů byla vypracována opět J. H. van Vleckem (srov. čl. 7.62).
b) Permitivita polárních látek
Díky tomu, že mechanické účinky elektrického a magnetického pole na elektrický a magnetický dipól jsou dány formálně shodnými vztahy, vzniká principiální možnost využít výsledky Langevinovy teorie též k určení orientační složky vektoru elektrické polarizace polárních dielektrik. Podmínkou její použitelnosti ovšem je, aby molekuly v dané látce byly dostatečně volné a mohly se účinkem elektrického pole natáčet.
Uvažujme látku obsahující n0 molekul v jednotce objemu a předpokládejme, že každá z těchto molekul má vlastní dipólový moment p 0. Pro orientační složku polarizace Pd bude na základě analogie s (7.66) a (7.67) jistě možné psát
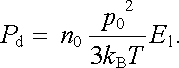 |
(7.69) |
V tomto vzorci E1 představuje intenzitu elektrického pole působícího na molekulu. Na rozdíl od problému paramagnetismu však zde není obecně možné zanedbat interakce mezi molekulami. Intenzita musí tedy mít význam lokálního pole. V analogii s článkem 7.6.1 můžeme zavést činitele orientační polarizovatelnosti
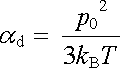 |
(7.70) |
a polarizovatelnost molekuly podle (7.48) zobecnit na tvar
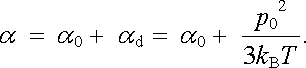 |
(7.71) |
Výsledek (7.71) , nazývaný Langevinovým-Debyeovým vzorcem, vyjadřuje, že celková polarizovatelnost látky je obecně dána součtem elektronové, atomové a orientační polarizovatelnosti. Orientační polarizovatelnost dává tedy zřejmě teplotně závislý příspěvek k celkové polarizovatelnosti a vzorec (7.71) dává také možnost vysvětlit pozorovaný typ teplotní závislosti permitivity (7.12) .
Z naměřené teplotní závislosti permitivity je na druhé straně principiálně možné pomocí (7.71) určit dipólový moment molekuly. V jednotlivých konkrétních případech však mohou nastat obtíže, které mohou vést k nesprávným výsledkům. Jedním zdrojem těchto obtíží je skutečnost, že pro výpočet lokálního pole polárních látek není obecně možné použít postup, který vede na Clausiovu-Mosottiovu formuli (srov. čl. 7.6.1). Kromě toho v pevných látkách mohou být molekuly vzájemně silně vázány, a mohou tudíž mít značně omezenou možnost orientování. Langevinova teorie pak není použitelná.
Uvažujme
homogenní vodič, který obsahuje jeden typ kladných a jeden typ záporných
nositelů proudu. Označíme-li postupně
 jejich koncentrace, q(+), q(-)
jejich náboje a v
(+)
, v
(-)
jejich střední (driftové) rychlosti, můžeme podle
(3.8)
až
(3.10)
vyjádřit
hustotu proudu j
ve tvaru
jejich koncentrace, q(+), q(-)
jejich náboje a v
(+)
, v
(-)
jejich střední (driftové) rychlosti, můžeme podle
(3.8)
až
(3.10)
vyjádřit
hustotu proudu j
ve tvaru
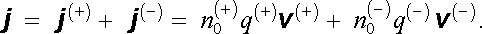 |
(7.72) |
Naším úkolem nyní bude vyšetřit relaci mezi rychlostmi v (+) , v (-) a intenzitou přiloženého pole E v těch případech, kdy platí Ohmův zákon.
Z Ohmova zákona vyplývá, že stacionární elektrické pole E může vybudit jen stacionární proud. Rychlosti v (+) , v (-) musí být tedy v tomto případě časově nezávislé. Kromě toho z požadavku platnosti Ohmova zákona vyplývá, že mezi těmito rychlostmi a intenzitou pole E musí platit úměrnost
 |
(7.73) |
Veličiny μ (+) , μ (-) jsou charakteristické pro daný vodič a nazývají se pohyblivostmi nositelů proudu. Pro platnost Ohmova zákona je ovšem nutné, aby pohyblivosti nezávisely na intenzitě pole.
Na druhé straně víme, že elektrické pole E působí na nositele náboje silami
 |
(7.74) |
nezávislými na jejich pohybu. Je proto zřejmé, že v látce musí na tyto nositele působit ještě další síly, které umožní současnou platnost vztahů (7.73) a (7.74) . Skutečně, kdyby takové síly neexistovaly, konstantní pole E by na nositele působilo nenulovými konstantními silami, které by vyvolaly jejich konstantní zrychlení. Nositelé proudu by se při konstantní intenzitě pole nemohly pohybovat konstantní rychlostí, takže by nemohly platit vztahy (7.73) nutné pro platnost Ohmova zákona.
Ohmův zákon požaduje, aby se nositelé proudu při působení konstantních elektrických sil (7.74) pohybovaly konstantními rychlostmi (7.73) . Z mechaniky víme, že taková situace je charakteristická pro pohyb těles ve viskózním prostředí, které klade pohybu těles odpor úměrný jejich rychlosti. Působení takových sil musíme tedy předpokládat také při pohybu nositelů proudu ve vodiči. Tyto "síly tření" mají původ v interakcích nositelů proudu s hmotou vodiče a mohou mít různé mechanismy v závislosti na typu těchto vodičů. Jejich existence je však pro platnost Ohmova zákona nutná. V těch případech, kdy bychom mohli nositele považovat za volné, by Ohmův zákon nemohl nikdy platit. (Srov. čl. 7.3.7; pro konvekční proud elektronů ve vakuu je charakteristická "třípolovinová" závislost proudu na přiloženém napětí.)
Dosazením (7.73) do (7.72) a srovnáním s Ohmovým zákonem (3.22) je možné vyjádřit měrnou vodivost
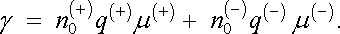 |
(7.75) |
Ve speciální, avšak časté situaci, kdy vodič jako celek je
neutrální, přičemž oba typy nositelů mají náboje stejné velikosti q(+) = q(-) = q, platí
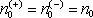 . Výraz
(7.75)
vyjadřující vodivost se
pak zjednodušší na tvar
. Výraz
(7.75)
vyjadřující vodivost se
pak zjednodušší na tvar
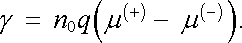 |
(7.76) |
Uvážíme-li dále, že platí μ (+) > 0, μ (-) < 0, můžeme jej dále přepsat. Dostaneme
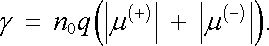 |
(7.76a) |
Pro látky
splňující Ohmův zákon platí vždy vztahy typu
(7.75)
a
(7.76)
. Koncentrace
nositelů proudu
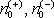 a jejich pohyblivosti μ
(+)
, μ
(-)
představují mikrofyzikální
parametry charakterizující elektrickou vodivost dané látky. Uvedené vztahy
také ukazují, kdy může být platnost Ohmova zákona narušena. Taková situace
nastane, jestliže koncentrace nositelů proudu, popřípadě jejich pohyblivost,
bude záviset na intenzitě přiloženého pole (popřípadě na hustotě procházejícího
proudu). Vztah
(7.75)
, resp.
(7.76)
nám také dovolí určit závislost měrné
vodivosti na teplotě popřípadě na jiných fyzikálních podmínkách, jestliže
zjistíme, jak na těchto podmínkách závisí obě zmíněné veličiny
a jejich pohyblivosti μ
(+)
, μ
(-)
představují mikrofyzikální
parametry charakterizující elektrickou vodivost dané látky. Uvedené vztahy
také ukazují, kdy může být platnost Ohmova zákona narušena. Taková situace
nastane, jestliže koncentrace nositelů proudu, popřípadě jejich pohyblivost,
bude záviset na intenzitě přiloženého pole (popřípadě na hustotě procházejícího
proudu). Vztah
(7.75)
, resp.
(7.76)
nám také dovolí určit závislost měrné
vodivosti na teplotě popřípadě na jiných fyzikálních podmínkách, jestliže
zjistíme, jak na těchto podmínkách závisí obě zmíněné veličiny
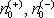 a μ
(+)
, μ
(-)
.
a μ
(+)
, μ
(-)
.
Je-li nám znám náboj nositelů proudu, je možné z měření měrné vodivosti určit pomocí (7.76) součin jejich koncentrace a pohyblivosti. Pro určení samotné hodnoty některé z těchto veličin je však třeba vedle vodivosti studovat ještě nějakou další vlastnost. V mnoha případech je velmi užitečné studovat Hallův jev (viz čl. 7.3.1), neboť jak ihned uvidíme, lze velmi jednoduše najít souvislost mezi Hallovou konstantou (respektive Hallovým odporem), nábojem a koncentrací nositelů proudu.
Na nositele proudu pohybující se ve vodiči umístěném v magnetickém poli působí totiž Lorentzova síla (3.57) . V geometrii podle obr. 7.18, kdy jsou nositelé proudu urychlováni elektrickým polem ve směru osy x, je nenulová jen její složka y, tj. FL,y = -qvxBz . Jelikož orientace FL,y závisí na znamení náboje, budou jejím účinkem nositelé proudu rozdělováni v příčném směru y, čímž vznikne elektrické pole Ey. V rovnovážném stavu musí platit qEy + FL,y = 0, odkud po dosazení z (7.19) dostaneme (za předpokladu jen jednoho typu nositelů) Ey = vxBz = jxBz/qn0. Srovnáním tohoto výsledku s experimentálním vztahem (7.19) můžeme pak vyjádřit Hallovu konstantu, respektive Hallův odpor hledanou relací
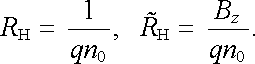 |
(7.77) |
V článku 7.1.3 byly vyloženy
nejdůležitější vlastnosti klasického modelu elektronového plynu. Použitím
tohoto modelu vyložíme nyní klasickou (Drudeho) teorii elektrické vodivosti
kovů. Podle tohoto modelu je v nulovém vnějším elektrickém poli pohyb elektronů
zcela chaotický, tj. střední hodnota složky rychlosti elektronu v libovolném
směru je nulová. V analogii s kinetickou teorií plynů se dále předpokládá, že
je možné tento chaotický pohyb elektronů charakterizovat
Maxwellovým-Boltzmannovým rozdělením rychlostí a že je možné zavést pojem
střední rychlosti
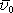 ,
střední volné dráhy
,
střední volné dráhy
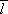 a střední doby volného pohybu
a střední doby volného pohybu
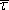 ,
které vyhovují vztahu
(7.6)
.
,
které vyhovují vztahu
(7.6)
.
Po přiložení vnějšího pole působí na každý elektron elektrická síla -eE , která vyvolává okamžité zrychlení a = -eE /me . Každý volný elektron tedy získává nenulovou složku rychlosti ve směru pole. Pro vznik makroskopického proudu je rozhodující její střední hodnota, kterou vypočteme na základě Drudeho elementární úvahy, vycházející z předpokladu, že při srážkách dochází ke středování směru rychlosti rovnoměrně do všech směrů.
Okamžitou rychlost vj (t) libovolného j-tého elektronu můžeme v každém okamžiku t vyjádřit vztahem
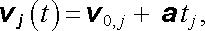 |
v němž v 0, j. značí rychlost, kterou měl uvažovaný elektron bezprostředně po poslední srážce a tj značí dobu, která uplynula od poslední srážky do uvažovaného okamžiku. Střední hodnotu rychlosti elektronů v daném okamžiku pak zřejmě dostaneme vystředováním vj (t) pro všechny elektrony v jednotce objemu
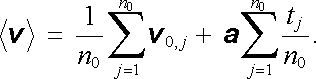 |
(7.78) |
První člen na pravé straně je roven nule díky uvedenému
středovacímu účinku srážek. Střední hodnota intervalu tj
má zřejmě význam střední doby volného pohybu
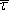 .
Platí tedy
.
Platí tedy
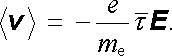 |
(7.79) |
Střední hodnota rychlosti je tedy úměrná intenzitě elektrického pole, jak žádá podmínka (7.73) . Pro pohyblivost elektronů dostáváme
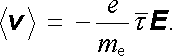 |
(7.80) |
Po dosazení do (7.75) můžeme vypočítat hustotu proudu a měrnou vodivost realizovanou volnými elektrony
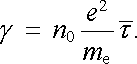 |
(7.81) |
V dosavadních úvahách jsme mlčky předpokládali, že střední doba volného pohybu nezávisí na intenzitě pole. Tento předpoklad, na němž závisí platnost Ohmova zákona, bude zřejmě splněn, jestliže dodatečná rychlost udělená elektronům elektrickým polem bude malá ve srovnání s rychlostí jejich tepelného neuspořádaného pohybu. Abychom získali konkrétní představu, uvedeme číselné hodnoty obou rychlostí pro případ mědi. Z úlohy Ú 7.8 plyne pro pohyblivost vodivostních elektronů mědi řádová hodnota 10-3 m2. s-1. V-1. Při v mědi již nedosažitelné intenzitě pole 103 V.m-1 (při níž by proudová hustota měla hodnotu ~ 1010 A.m-2) by tedy elektronům byla udělována rychlost jednoho metru za sekundu. Naproti tomu pro střední rychlost neuspořádaného pohybu plyne z ekvipartičního teorému (viz např. [10]) pro pokojovou teplotu řádový odhad 104 m.s-1 a kvantově mechanický odhad dává pro pás šířky 10 eV hodnotu 106 m.s-1 (srov. čl. 7.1.2). Uvedený předpoklad je tedy pro měď bohatě splněn. Podobnými odhady bychom se mohli o jeho platnosti přesvědčit i pro jiné kovy. Drudeho teorie tedy podává realistický obraz o podmínkách platnosti Ohmova zákona v kovech.
Na jejím základě je možné úspěšné vyložit i platnost Franzova-Wiedemannova zákona (viz čl. 7.3.2). Aplikací metod kinetické teorie je totiž možné rovněž vypočítat příspěvek volných elektronů k tepelné vodivosti kovů, který často hraje dominantní úlohu (srov. způsob výpočtu tepelné vodivosti plynů uvedený například v [10]). Příslušný výpočet ukazuje,[72] že tepelnou vodivost elektronového plynu Λ e lze vyjádřit vztahem
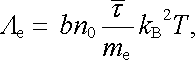 |
(7.82) |
v němž T představuje absolutní teplotu, kB Boltzmannovu konstantu a b číselnou konstantu b B 3. Využitím (7.81) a (7.82) pro poměr elektrické a tepelné vodivosti dostáváme
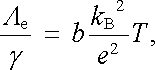 |
(7.83) |
což je vztah shodný s experimentálním výrazem
(7.26)
.
Jelikož platí
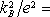 0,743.10-8 W.Ω
.K-2,
vidíme, že
(7.83)
dává i vcelku dobrý kvantitativní souhlas s experimentem.
0,743.10-8 W.Ω
.K-2,
vidíme, že
(7.83)
dává i vcelku dobrý kvantitativní souhlas s experimentem.
Ve výkladu dalších fyzikálních vlastností kovů však klasický model elektronového plynu již nebyl zdaleka tak úspěšný. V článku 7.2.2 jsme například viděli, že v rozporu s experimentem předpovídá teplotně závislou paramagnetickou susceptibilitu vodivostních elektronů. Podobná situace nastává i v případě měrného tepla. Podle klasického modelu by elektronový plyn měl mít značnou tepelnou kapacitu a měrné teplo kovů by i za vyšších teplot mělo být značně větší než měrné teplo nekovů. Ve skutečnosti však mají oba typy látek měrná tepla v podstatě stejná. Jak ukázal A. Sommerfeld, uvedené rozpory plynou z omezené použitelnosti Maxwellova-Boltzmannova rozdělení. Při použití Fermiho-Diracova rozdělení vystihuje model elektronového plynu správně situaci i v případě uvedených vlastností. Je totiž zřejmé, že na měrném teple i na paramagnetické susceptibilitě se může podílet jen malý počet elektronů s energií blízkou Fermiho energii.
V oddílu 7.4 bylo ukázáno, že pro vodivost roztoků je charakteristická platnost Ohmova zákona a existence elektrolýzy vedla již Faradaye k závěru, že nositeli proudu v roztocích jsou hmotné částice (ionty) v roztoku přítomné. S. Arrhenius objasnil později (r. 1887) vznik těchto iontů jako důsledek štěpení molekul elektrolytu, které nastává působením rozpouštědla. Podle Arrhenia jsou molekuly elektrolytu v roztoku vždy v menší či větší míře rozštěpeny na kladné a záporné ionty, bez ohledu na to, teče-li roztokem proud.
Štěpení, tj. elektrolytická disociace, molekul je tedy důsledek vzájemné interakce mezi molekulami elektrolytu a rozpouštědla[73] . V daném roztoku tedy existuje vždy určitá koncentrace kladných a záporných nositelů proudu, která je určena pouze druhem látek tvořících roztok, jeho koncentrací, teplotou a případně jinými fyzikálními podmínkami. Na vzniku nositelů proudu se však za normálních podmínek nepodílí přiložené elektrické pole. Toto pole se podílí na vzniku elektrického proudu pouze tím, že uvádí již existující nositele proudu do pohybu.
Jak jsme viděli v článku 7.6.4, je pro platnost Ohmova zákona nutná vedle nezávislosti koncentrace nositelů proudu na intenzitě pole i obdobná nezávislost jejich pohyblivosti. Tento požadavek je však v případě roztoku zřejmé dobře splněn, neboť lze přirozeně předpokládat, že každý iont je "hustě" obklopen molekulami rozpouštědla, které mu brání v pohybu. Pohyb iontu v roztoku můžeme tedy s dobrým přiblížením považovat za pohyb tělesa ve spojitém viskózním prostředí, který může být popsán známým Stokesovým vzorcem. Platnost Ohmova zákona je pak již zřejmá. V nejčastějším případě, kdy se molekula štěpí na dva ionty opačné polarity se stejnou absolutní hodnotou náboje q, je možné vyjádřit měrnou vodivost vztahem (7.76a)
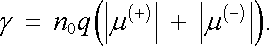 |
Pohyblivosti iontů μ (+) , μ (-) musí být zpravidla určovány experimentálně (srov. úlohy Ú 7.13 a Ú 7.14). K tomu účelu je výhodné určit jejich vztah k Hittorfovým převodním číslům. Použitím definičního vztahu (7.46) dostaneme podle (7.76a)
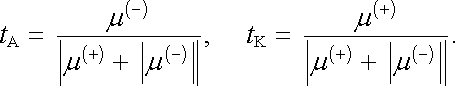 |
(7.84) |
Jak bylo již řečeno v čl. 7.4.1, má pro studium vlastností roztoků zvlášť velký význam zjišťovat pohyblivosti při nízkých koncentracích, kdy je možné zanedbat vzájemné interakce mezi ionty elektrolytu. Nejčastěji se užívají hodnoty při "nekonečném zředění", tj. hodnoty extrapolované k nulové koncentraci.
Představa o iontech jako nositelích proudu v roztocích umožňuje také velmi jednoduše vyložit platnost Faradayových zákonů elektrolýzy, které (jak uvidíme) jsou bezprostředním důsledkem Avogadrova zákona. Nechť při projití náboje Q roztokem se vyloučí určité množství látky o hmotnosti M. Jestliže každý iont nese z elementárních nábojů, je k přenesení náboje Q zapotřebí n = Q/ez iontů. Jejich celkovou hmotnost můžeme snadno vyjádřit pomocí Avogadrova zákona vztahem M = Am n/ N0 , v němž N0 je Avogadrova konstanta a Am relativní molekulová hmotnost iontu. Pro hmotnost M pak platí vztah
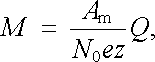 |
(7.85) |
který má již tvar prvního Faradayova zákona (7.44) . Pro elektrochemický ekvivalent přitom vychází
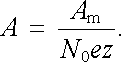 |
(7.86) |
Ze vzorce (7.85) také ihned vyplývá vztah (7.45) , vyjadřující druhý Faradayův zákon. Faradayův náboj F = N0 e, zavedený v čl.7.4.2, představuje skutečně univerzální konstantu.
Nyní se pokusíme vyložit koncentrační závislost měrné vodivosti pomocí Arrheniovy teorie disociace. Zanedbáme-li totiž v prvním přiblížení koncentrační závislost pohyblivosti, bude závislost měrné vodivosti dána právě jen koncentrační závislostí hustoty nositelů proudu, tj. bude výrazně záviset na tom, jak se s koncentrací mění stupeň disociace elektrolytu.
Arrheniova teorie vychází z předpokladu, že v daném roztoku probíhá neustále jednak proces disociace dosud nedisociovaných molekul, jednak proces rekombinace, při němž se ionty elektrolytu spojují opět v elektricky neutrální molekulu. V rovnovážném stavu se rychlost obou procesů vyrovná, takže se celkový počet disociovaných molekul v roztoku již s časem nemění.
Předpokládejme, že dané koncentraci roztoku odpovídá c molekul elektrolytu v jednotce objemu. Pro popis disociačního stupně zaveďme veličinu α vyjadřující relativní počet disociovaných molekul. Počet disociovaných molekul v jednotce objemu tedy bude α c, zatímco počet nedisociovaných bude (1 - α )c. Předpokládejme nyní, že proces disociace probíhá s pravděpodobností p. Počet molekul Δ n ℜ' , které v jednotce objemu disociují za jednotku času, bude pak možno vyjádřit vztahem Δ n ℜ' = (1 - α )cp. Obráceně předpokládejme, že proces rekombinace probíhá s pravděpodobností q. Počet molekul Δ n ℜ'ℜ' rekombinujících v jednotce objemu za jednotku času bude zřejmě úměrný jak koncentraci aniontů, tak koncentraci kationtů. Bude tedy platit Δ n ℜ'ℜ' = qα 2c2. Z podmínky rovnováhy Δ n ℜ' = Δ n ℜ'ℜ' dostaneme podmínku pro veličinu α
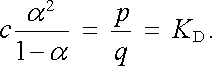 |
(7.87) |
Veličina KD podle předpokladu nezávisí již na koncentraci roztoku. Vyjadřuje schopnost daného elektrolytu disociovat v daném rozpouštědle a nazývá se jeho disociační konstantou.
Vztah (7.87) představuje kvadratickou rovnici, ze které může být vypočítána rovnovážná hodnota činitele disociace α .. Speciálně pro velmi malé koncentrace plyne z (7.87)
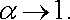 |
(7.88) |
Disociační stupeň α se s klesající koncentrací blíží jedné. V oboru platnosti vztahu (7.88) tedy měrná vodivost roztoku poroste úměrně s jeho koncentrací. Tato závislost je ve shodě s experimentálními výsledky znázorněné na obr. 7.36. V oboru vyšších koncentrací však již nelze naměřené koncentrační závislosti vodivosti na základě řešení rovnice (7.87) vysvětlit. Jedním z důvodů je, že nelze zanedbat závislost pohyblivosti na koncentraci.
Disociační stupeň α má velmi jednoduchý vztah k molární vodivosti. Přímo z její definice vyplývá tzv. Arrheniův vztah
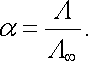 |
(7.89) |
Disociační stupeň α při dané koncentraci je tedy určen poměrem molárních vodivostí při této koncentraci a při nekonečném zředění. Vezmeme-li v úvahu vzorec (7.89) , můžeme rovnici (7.87) přepsat na tvar
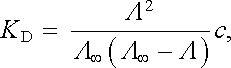 |
(7.90) |
nazývaný Ostwaldovým zřeďovacím zákonem.
Právě vyložená teorie disociační rovnováhy platí pouze pro slabé elektrolyty. V případě silných elektrolytů totiž existují důvody k předpokladu, že i při konečných (a někdy značně vysokých) koncentracích roztoků jsou téměř všechny molekuly elektrolytu disociovány, takže pojem disociační rovnováhy přestává mít smysl. Východiskem pro přesnější popis chování silných elektrolytů je teorie vypracovaná P. Debyem a E. Hückelem (v r. 1923), která se stala základem pozdějších interpretací vlastností především silných elektrolytů. Tato teorie je založena na modelu mikroskopického popisu elektrické interakce mezi ionty v ionizovaném prostředí, zatímco interakce jiného typu zanedbává. Uvažovaný iont je pokládán za bodový náboj, jehož interakce s nejbližšími ionty má charakter Coulombova zákona a vzdálenější ionizované prostředí je považováno za elektricky aktivní kontinuum reagující na přítomné makroskopické elektrické pole. Model předpokládá, že uvažovaný iont vyvolá - elektrostatickou interakcí s nejbližšími ionty - přerozdělení jejich poloh tak, že náboj uvažovaného iontu bude do značné míry odstíněn. Z příslušného výpočtu vyplývá, že na stínění se podílí ionty, jejichž vzdálenost od uvažovaného iontu je menší než jistá veličina λ D, nazývaná Debyeův-Hűckelův poloměr [74] .
Debyeovu-Hückelovu teorii lze aplikovat nejen na chování elektrolytů, ale také na chování plazmatu. Její podrobnější výklad však přesahuje rámec této knihy. Pro podrobnější poučení odkazujeme na obšírnější učebnice či monografie věnované statistické fyzice74, a také na učebnice fyzikální chemie [13, 16].
Základní vlastnosti nesamostatného výboje vyložené v článku 7.5.1 (zejména značná závislost nasyceného proudu na vnějších vlivech) ukazují, že za podmínek nesamostatného výboje jsou v plynu přítomni nositelé proudu, jejichž koncentrace je určena vnějšími faktory působícími na plyn.
V plynu se mohou principiálně vyskytovat tři typy nositelů proudu: kladné a záporné ionty a volné elektrony. Při nesamostatném výboji je nutné předpokládat, že všechny typy nositelů vznikají ionizací molekul plynu. V oddílu 7.1 jsme uvedli základní fakta o procesech ionizace atomů a molekul, ze kterých vyplynulo, že různé typy látek mají různé ionizační vlastnosti. Podíl jednotlivých typů nositelů na celkové vodivosti plynu bude tedy záviset především na typu plynu. Ukazuje se však, že závisí rovněž na tlaku.
Bylo prokázáno (srov. rovněž výklad o Franckově-Hertzově pokusu v článku 7.5.2), že k ionizaci molekuly může dojít při nepružné srážce s jinou částicí (elektronem, iontem apod.) o dostatečně vysoké energii, při níž ionizovaná molekula přijímá určité množství energie potřebné například k vyražení jednoho elektronu. K vytržení jednoho elektronu z atomu či molekuly může také dojít při dopadu fotonu o dostatečně vysoké energii. Ionizační účinky bude mít proto především záření krátkovlnné (ultrafialové, rentgenové, záření gama). V oddílu 7.1 byla rovněž diskutována možnost vzniku záporného iontu, která je pro různé typy částic různá. Možnost vzniku záporného iontu daného typu bude zřejmě závislá na vzájemné rychlosti molekuly a elektronu.
Uvedené poznatky dovolují předpokládat, že v plynu existuje vždy určitá koncentrace volných elektronů a iontů, která je dána dynamickou rovnováhou mezi procesem ionizace a procesem rekombinace, při němž vznikají zpětně neutrální molekuly. Na základě diskuse této rovnováhy je možné popsat vlastnosti nesamostatného výboje.
Pro zjednodušení
budeme uvažovat situaci v inertním plynu, v němž se nachází pouze kladné ionty
a volné elektrony. Předpokládejme, že účinkem vnějších ionizačních činitelů
(nezávislých na přiloženém vnějším poli) se v jednotce objemu ionizuje za
jednotku času Δ
n
atomů. Vznikne tedy Δ
n
kladných iontů a Δ
n
volných
elektronů. Zaveďme činitel rekombinace Kr, který vyjadřuje pravděpodobnost,
že za jednotku času dojde v plynu k rekombinaci iontu s volným elektronem, a
tedy ke vzniku neutrálního atomu (srov. úlohu Ú 7.17). Počet rekombinaci Δ
n
ℜ'
,
které nastanou v jednotce objemu za jednotku času, bude zřejmě úměrný jak
koncentraci iontů
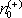 , tak koncentraci volných elektronů
, tak koncentraci volných elektronů
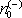 . Jelikož za našich předpokladů je
. Jelikož za našich předpokladů je
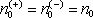 , bude platit
, bude platit
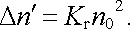 |
(7.91) |
Podmínka rovnováhy Δ n = Δ n ℜ' tedy dává
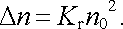 |
(7.92) |
Z ní je možné rovnovážnou koncentraci iontů a volných elektronů vypočítat.
Uvažujme nyní plyn vyplňující prostor mezi dvojicí rovinných rovnoběžných elektrod plochy S, umístěných ve vzájemné vzdálenosti d, na nichž je přiloženo napětí U. Pole E = U/d bude urychlovat elektrony a ionty v plynu a mezi elektrodami poteče jistý proud I. To ovšem znamená, že část nositelů proudu bude odevzdávat svůj náboj na elektrodách, čímž se bude jejich koncentrace zmenšovat. Předpokládejme, že v jednotce objemu ubude za jednotku času tímto způsobem Δ n ℜ'ℜ' nositelů. Místo (7.92) bude nyní platit obecnější podmínka rovnováhy tvaru
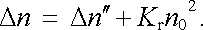 |
(7.93) |
Nyní vyšetříme dvě mezní situace. Při malých hodnotách napětí U bude zřejmě Δ n ℜ'ℜ' << Δ n ℜ' . Úbytek nosičů proudu bude dán převážně jejich rekombinací. Rovnovážná koncentrace n0 bude dána opět podmínkou (7.92) a nebude téměř závislá na protékajícím proudu. Za této situace bude možné vedení proudu popsat stejným modelem, který jsme použili v čl. 7.6.5 při vyšetřování vodivosti elektronového plynu. Pohyblivost μ nositelů proudu daného typu bude dána vztahem
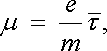 |
(7.94) |
který je analogický k
(7.80)
a v němž m představuje hmotnost částice a
 střední dobu jejího volného pohybu. Pro
vedení proudu bude platit Ohmův zákon. Vyšetřovaná situace zřejmě odpovídá
oblasti (a) na obr. 7.41.
střední dobu jejího volného pohybu. Pro
vedení proudu bude platit Ohmův zákon. Vyšetřovaná situace zřejmě odpovídá
oblasti (a) na obr. 7.41.
Pro velké hodnoty napětí U dostaneme druhý mezní případ, kdy budou téměř všichni nositelé proudu přitaženi k elektrodám dříve, než budou mít možnost rekombinovat. V tomto případě bude Δ n ℜ'ℜ' >> Δ n ℜ' a podmínka rovnováhy bude mít tvar
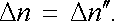 |
(7.95) |
Z ní vyplývá, že proud mezi elektrodami má konstantní hodnotu I, nezávislou na změně napětí U. Předpokládáme-li, že dané částice nesou náboj ez dostaneme
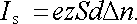 |
(7.96) |
Proud Is je maximální proud, který může při daných ionizačních mechanismech plynem projít. Dostáváme tedy situaci odpovídající oblasti (c) na obr. 7.41.
Předpokládejme nyní, že napětí U přiložené na elektrody je dále zvyšováno. Je zřejmé, že ke kvalitativní změně situace v plynu dojde při takových jeho hodnotách, při nichž elektron (resp. iont) získá od elektrického pole za dobu svého pohybu mezi po sobě následujícími srážkami kinetickou energii srovnatelnou s energií ionizační. Za těchto podmínek počne vzrůstat počet nepružných srážek uvažované nabité částice s neutrálními molekulami, takže daný elektron (resp. iont) počne produkovat další páry nositelů proudu. Kromě toho mohou kladné ionty dopadající na katodu vyvolat sekundární emisi elektronů, čímž koncentrace nositelů proudu v plynu rovněž vzroste.
Uvedené mechanismy vzniku nosičů proudu, na nichž se podílí
přiložené elektrické pole, jsou zřejmě odpovědné za vzrůst proudové hustoty v
oblasti (d) charakteristiky z obr. 7.41 a při určité kritické hodnotě
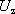 přiloženého napětí vedou k lavinovitému
vzrůstu koncentrace nosičů proudu, a tudíž k nasazení (zapálení) samostatného
výboje. Uvědomíme-li si, že střední volná dráha molekul plynu
přiloženého napětí vedou k lavinovitému
vzrůstu koncentrace nosičů proudu, a tudíž k nasazení (zapálení) samostatného
výboje. Uvědomíme-li si, že střední volná dráha molekul plynu
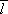 je nepřímo úměrná tlaku,
je nepřímo úměrná tlaku,
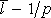 , a pro intenzitu pole můžeme psát E = U/d, kde d je vzdálenost elektrod, pak z požadavku rovnosti ionizační energie
Wi a práce elektrického pole na dráze
, a pro intenzitu pole můžeme psát E = U/d, kde d je vzdálenost elektrod, pak z požadavku rovnosti ionizační energie
Wi a práce elektrického pole na dráze
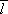 ,
,
 , můžeme odhadnout podmínky pro
nasazení samostatného výboje. Z uvedených vztahů vyplývá, že zápalné napětí Uz
bude funkcí součinu tlaku plynu a vzdálenosti elektrod, což je také obsahem
experimentálně zjištěného Paschenova zákona.
, můžeme odhadnout podmínky pro
nasazení samostatného výboje. Z uvedených vztahů vyplývá, že zápalné napětí Uz
bude funkcí součinu tlaku plynu a vzdálenosti elektrod, což je také obsahem
experimentálně zjištěného Paschenova zákona.
ÚLOHY KE KAPITOLE 7
Ú
7.1: Předpokládejte, že atom vodíku je tvořen protonem, kolem nějž obíhá
elektron konstantní úhlovou rychlostí ω
po rovinné kruhové
dráze o poloměru r = 0,1 nm, a že
působení mezi protonem a elektronem lze popsat Coulombovým zákonem. Užitím
tohoto zjednodušeného modelu vypočítejte koeficient polarizovatelnosti
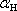 atomu
vodíku za předpokladu, že elektrické pole působící na atom je kolmé k rovině dráhy elektronu. Získanou hodnotu
α
H
porovnejte
s hodnotou určenou z
naměřené relativní permitivity molekulárního vodíku ε
r = 1,00026
při hustotě ρ
M = 0,04
kg. m-3.
atomu
vodíku za předpokladu, že elektrické pole působící na atom je kolmé k rovině dráhy elektronu. Získanou hodnotu
α
H
porovnejte
s hodnotou určenou z
naměřené relativní permitivity molekulárního vodíku ε
r = 1,00026
při hustotě ρ
M = 0,04
kg. m-3.
Ú 7.2: Jaká je polarizovatelnost molekuly benzenu C6H6, jestliže při teplotě 20 °C byla naměřena relativní permitivita ε r = 2,2773. Benzen je nepolární a při teplotě 20 °C má hustotu ρ M = 879,0 kg. m-3.
Ú 7.3: Experimentálně zjištěná teplotní závislost relativní permitivity ε r vodních par je uvedena v tabulce 7.12. Předpokládejte, že vodní pára se chová jako ideální plyn, a vypočítejte teplotní závislost její molární polarizace. Určete polarizovatelnost molekuly vody a její dipólový moment.
Tabulka 7.12 Teplotní závislost permitivity vodních par.
|
T (K) |
393 |
423 |
453 |
483 |
|
tlak (Pa) |
75 300 |
81 210 |
87 100 |
92 970 |
|
(r - 1) . 105 |
400,2 |
371,7 |
348,8 |
328,7 |
Ú 7.4: Válcová nádoba velmi malé podstavy o výšce l cm je naplněna kapalným chlorovodíkem HCl o hustotě 1710 kg. m-3. Molekula HCl má vlastní elektrický dipólový moment p = 4,44 .10-30 C. m. Určete velikost polarizace P a celkový dipólový moment pV za předpokladu, že dipólové momenty všech molekul jsou orientovány ve směru osy nádobky.
Ú 7.5: Dvě kuličky malých rozměrů, z nichž jedna je hliníková a druhá bismutová, jsou zavěšeny v nehomogenním magnetickém poli, které má nenulový gradient ve směru spojnice středů kuliček. Obě tělesa se dotýkají a gradient magnetického pole je v celém jejich objemu konstantní. Určete pořadí umístění kuliček a vztah mezi jejich poloměry RBi, RAl tak, aby výsledná síla působící na kuličky byla nulová.
Ú 7.6: Železo má kubickou, objemově centrovanou krystalovou mřížku s mřížkovou konstantou a0 = 0,286 nm. Pro kovové železo bylo experimentálně zjištěno, že magnetický moment připadající na jeden atom při 0 K je 2,216 μ B. Určete odpovídající spontánní magnetizaci (respektive magnetickou polarizaci) železa.
Ú 7.7: Nekovové paramagnetikum obsahuje v jednotce objemu n0 atomů s lokalizovaným magnetickým momentem 1 μ B. Látka je umístěna v magnetickém poli l T při teplotě 300 K. Určete počet atomů Δ n0 , které by vytvářely stejnou magnetizaci za předpokladu, že jejich momenty jsou zcela orientovány ve směru pole.
Ú 7.8: Vypočtěte pohyblivost volných elektronů v mědi za předpokladu, že na každý atom připadá jeden vodivostní elektron. Při výpočtu vyjděte z hodnoty měrné vodivosti podle tab. 7.7.
Ú 7.9: Vypočtěte pohyblivost nositelů proudu v germaniu s příměsí arsenu o koncentraci 1,5 . 1015 donorů/cm3. Měrná vodivost γ = 1 Ω -1cm-1.
Ú
7.10: Při měření Hallova jevu v kovovém sodíku bylo při proudové hustotě j = 107A.m-2 a
magnetickém poli B = 1 T naměřeno
příčné elektrické pole
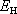 = 2,5
.10-3
V.m-1. Určete koncentraci vodivostních elektronů n0, porovnejte ji s počtem atomů v 1 m3.
Hustota sodíku je 970 kg. m-3
= 2,5
.10-3
V.m-1. Určete koncentraci vodivostních elektronů n0, porovnejte ji s počtem atomů v 1 m3.
Hustota sodíku je 970 kg. m-3
Ú 7.11: Jaká je výstupní práce elektronů daného kovu, jestliže při zvýšení teploty z 2000 K na 2001 K se nasycený emisní proud zvýší o l %?
Ú
7.12: Roztok KCl o koncentraci 10% má měrný odpor ρ
R = 0,074
Určete stupeň disociace, jsou-li pohyblivosti iontů
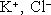 ve vodě rovny:
ve vodě rovny:
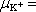 6,7
. 10-8 m2.s-1.V-1,
6,7
. 10-8 m2.s-1.V-1,
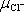 = 6,8 . 10-8 m2.s-1.V-1.
= 6,8 . 10-8 m2.s-1.V-1.
Ú
7.13: Určete stupeň disociace a měrný odpor čisté vody, jsou-li známé rovnovážné
koncentrace iontů H+ a OH- rovné 10-4 mol.m-3
a pohyblivosti těchto iontů
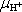 = 3,2 . 10-7 m2.s-1
V-1,
= 3,2 . 10-7 m2.s-1
V-1,
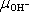 = 1,8 . 10-7 m2.s-1
V-1.
= 1,8 . 10-7 m2.s-1
V-1.
Ú 7.14: Při elektrolýze zředěného roztoku NaCl v přístroji pro stanovení Hittorfových převodních čísel byl zjištěn úbytek elektrolytu u anody 0,4 molu, prošel-li přístrojem náboj rovný Faradayovu náboji F. Molární vodivost roztoku NaCl při nekonečném zředění Λ ℜ nekonecno = 12,6 m2 >-1.mol-1, teplota roztoku byla 25 °C. Stanovte pohyblivostí iontů Na+, Cl-.
Ú
7.15: Extrapolováním koncentrační závislosti molární vodivosti vodných roztoků
HC1, NaCl a octanu sodného byly nalezeny molární vodivosti při nekonečném zředění (při teplotě 25
°C):
Λ
ℜ nekonecno
,HCl
= 42,4 m2.>-1.mol-1,
Λ
ℜ nekonecno
,NaCl
= 12,6
m2.>-1.mol-1,
 = 9,2 m2.>-1.mol-1.
Vypočtěte hodnotu Λ
ℜ nekonecno
pro kyselinu octovou CH3COOH, pro níž
nelze extrapolaci v zásadě provést, a to pro neúplnou disociaci při velkých
zředěních.
= 9,2 m2.>-1.mol-1.
Vypočtěte hodnotu Λ
ℜ nekonecno
pro kyselinu octovou CH3COOH, pro níž
nelze extrapolaci v zásadě provést, a to pro neúplnou disociaci při velkých
zředěních.
Ú 7.16: Určete měrný odpor vzduchu za normálního tlaku a teploty, jestliže díky přirozené radioaktivitě a kosmickému záření vzniká v 1 m3 za každou sekundu 5.106 iontových párů.
Ú 7.17 Vzduch mezi deskami rovinného kondenzátoru je účinkem ionizujícího záření ionizován homogenně v celém objemu. Za jednotkou času vzniká v objemové jednotce Δ n iontových párů. Obě desky kondenzátoru jsou uzemněny, v prostoru mezi elektrodami je ustavena rovnováha mezi ionizací a rekombinací, která je určena činitelem rekombinace Kr. Stanovte:
a) rovnovážnou koncentraci iontových párů n0,
b) časovou závislost koncentrace iontových párů n(t) po vypnutí ionizujícího záření,
c) uvažte, jak by bylo možné využít závislosti n(t) k měření činitele rekombinace Kr.
[47] V literatuře je frekventovanější tzv. Rydbergova konstanta Rℜ nekonecno B 1,0973 m-1, pro niž platí R ω = 2π cRℜ nekonecno . Podrobnější údaje o významu těchto veličin najde čtenář například v [2].
[48] Existence spinu elektronu neplyne z kvantové mechaniky v nerelativistickém přiblížení. Jeho existence a vlastnosti byly v letech 1925-1927 dodatečně postulovány pro vysvětlení pozorovaných experimentálních faktů. Později (v r. 1928) vyplynula existence spinu elektronu z Diracovy relativistické teorie.
[49] Jde o experimentálně zjištěné hodnoty převzaté z publikace Tablicy fizičeskich veličin, redaktor I. K. Kikoin, Atomizdat, Moskva 1967.
[50] Sledujeme volně výklad uvedený v knize V. Frei: Fyzika pevných látek. SPN, Praha 1978.
[51] Hustota pravděpodobnosti fB( v ) nezávisí ovšem na směru rychlosti v . Častěji se proto vyjadřuje hustota pravděpodobnosti g( v ) pro rychlost o dané velikosti v . Platí pro ni vztah
(7.5a)
nazývaný Maxwellovým-Boltzmannovým rozdělením.
[52] Odvození vztahu (7.7) lze nalézt ve standardních učebnicích statistické fyziky. Odvození normovací konstanty v (7.8) spíše v elementárních učebnicích fyziky pevných látek. V českém jazyce viz například A. J. Dekker: Fyzika pevných látek. Academia, Praha 1966, nebo C. Kittel: Introduction to Solid State Physics, český překlad Úvod do fyziky pevných látek. Academia, Praha 1985.
[53] K podrobnějšímu studiu doporučujeme učebnice fyziky pevných látek. V českém jazyce například učebnici Ch. Kittel: Úvod do fyziky pevných látek. Academia, Praha 1985.
[54] Výjimku tvoří supravodice; tzv. supravodiče I. typu (viz čl. 7.3.5) je možné považovat za ideální diamagnetika, pro něž platí χ m = -1. Jejich relativní permeabilita je tedy nulová.
[55] Pro klasické magneticky uspořádané materiály byla téměř vždy charakteristická dobře vyvinutá krystalická struktura, tj. jednalo se buď o monokrystaly, nebo o látky polykrystalické s dobře vyvinutými monokrystalickými zrny, na jejichž prostorovou orientaci je vázána orientace spontánně uspořádaných magnetických momentů. V posledních letech však nabývá značný význam i skupina magneticky uspořádaných materiálů nanokrystalických či amorfních. Zvláštní třídu tvoří tzv. spinová skla, pro něž je charakteristická prostorová izotropie spontánní magnetizace.
[56] Například pro klasická feromagnetika železo, kobalt, nikl a gadolinium platí postupně: TC(Fe) = 1043 K, (Fe) = 1090 K, TC(Co) = 1393 K, (Co) = 1420 K, TC(Ni) = 631 K, (Ni) = 650 K, TC(Gd) = 289 K, (Gd) = 303 K.
[57] Z látek jiných skupenství je iontová vodivost charakteristická pro kapalné roztoky a za určitých podmínek také pro plyny. V plynech se však při silných elektrických polích významně uplatňuje i vodivost elektronová. V koloidních roztocích mohou být nositeli proudu dokonce i makroskopické částice.
[58] V roce 1980 byl na speciální polovodičové součástce objeven tzv. kvantový Hallův jev (a následně již v roce 1982 na podobném systému tzv. zlomkový kvantový Hallův jev). Kvantový Hallův jev, který souvisí s charakterem kvantování elektronových stavů v dvoudimezionálních elektronových systémech, spočívá v existenci prodlev v závislosti Hallova odporu na magnetickém poli při velmi nízkých teplotách. Jak se ukázalo, prodlevy mají přímou souvislost se změnami v obsazování jednotlivých elektronových stavů a jejich vzdálenost je přímo určena jednak hodnotou Planckovy konstanty a jednak nábojem nositelů proudu. Oba zmíněné jevy mají velký význam pro studium nízkodimenzinálních elektronových soustav připravovaných nejčastěji heterostrukturní technologií (srov. čl. 7.3.4). Vedle toho má dnes kvantový Hallův jev velký význam i pro metrologii jako.normál odporu. Pro studium metrologických hledisek odkazujeme na knihu J. Brož, V. Roskovec: Základní fyzikální konstanty. SPN, Praha 1988, pro obecné poučení na monografii J. D. Davis: The Physics of Low-Dimensional Semiconductors. Cambridge University Press, Cambridge 1999.
[59] Grüneisenův vztah nebere ovšem v úvahu existenci supravodivosti, která nastává u některých kovů při nízkých teplotách. Supravodivostí se budeme zabývat v článku 7.3.5.
[60] Údaje pro obr. 7.19 byly převzaty ze znamenité učebnice Ch. Kittela: Introduction to Solid State Physics. J. Wiley 1968, která existuje rovněž v českém překladu (Ch. Kittel: Úvod do fyziky pevných látek. Academia, Praha 1985) a kterou doporučujeme k dalšímu studiu. V této učebnici lze rovněž nalézt podrobnější informace o Grüneisenově vztahu a o Grüneisenově funkci.
[61] Charakter příměsové vodivosti polovodiče přímo souvisí s vlastnostmi Fermiho-Diracova rozdělení a zej-ména s vlivem příměsí na hodnotu chemického potenciálu - srov. čl. 7.1.3.
[62] Z české literatury doporučujeme ke studiu knihu H. Frank: Fyzika techniky polovodičů. SNTL, Praha 1990. Nejnovější poznatky o rozvoji tohoto velmi dynamického oboru lze ovšem nalézt jen v časopiseké literatuře.
[63] Graf na obr. 7.31 je převzat z textu přednášky H. Kammerlinga Onnese při příležitosti převzetí Nobelovy ceny za fyziku v roce 1913. Viz sborník Nobel Lectures, Physics (1901-1921). Elsevier Publ. Comp., Amsterdam 1962.
[64] Bylo zjištěno, že magnetické pole může vniknout jen do tenké povrchové vrstvy supravodiče, jejíž tloušťka je v řádu 10-7 m. Jako dostatečně rozměrný supravodič musíme chápat takový vzorek, jehož všechny rozměry podstatně přesahují uvedenou hodnotu. Meissnerův-Ochsenfeldův jev reprezentuje formální analogii mezi chováním supravodiče v magnetickém poli a vodiče v poli elektrostatickém.
[65] Pro podrobnější obecné poučení o problematice supravodivosti doporučujeme publikaci R. S. Šafrata a kol.: Fyzika nízkých teplot. Matfyzpress, Praha 1998; pro poučení o využití Josepsonova jevu k metrologickým účelům doporučujeme knihu [2] (J. Brož, V. Roskovec: Základní fyzikální konstanty. SPN, Praha 1988).
[66] Chemickým ekvivalentem G se rozumí formální z-tý díl molekuly nebo jiné uvažované částice, kde z je buď počet přijatých, nebo odevzdaných elektronů v dané oxidačně redukční reakci, nebo udává celkový počet elementárních nábojů kationtů vyměněných touto molekulou (částicí) v reakci jiného typu. Dříve se číslo z zjednodušeně nazývalo valencí. Pro jeden mol chemických ekvivalentů se dříve užívala jednotka jeden val. Například jeden mol chemických ekvivalentů (val) kyseliny chlorovodíkové HC1 je totožný s molem HC1, neboť v reakcích s HC1 se nahrazuje pouze jeden atom vodíku. Naproti tomu v případě kyseliny sírové H2SO4 v reakcích, v nichž se nahrazují oba vodíkové atomy, je jeden mol chemických ekvivalentů (val) H2SO4 roven polovině molu H2SO4. Molární vodivost vztahovaná na jednotkovou molární koncentraci chemických ekvivalentů se dříve nazývala ekvivalentová vodivost.
[67] Podle terminologie zavedené ve fyzikální chemii se reakce zabezpečující odčerpávání elektronů z elektrody nazývá katodickou reakcí naopak reakce zabezpečující předávání elektronů elektodě se nazývá reakcí anodickou.
[68] Za stacionární považujeme výboj, který je (při konstantním přiloženém napětí) charakterizován stacionární proudovou hustotou. Vedle doutnavého a obloukového výboje existuje řada dalších forem stacionární samostatné vodivosti plynů. Nejznámějším příkladem nestacionárního výboje je výboj jiskrový, který nastává například v plynu o tlaku blízkém atmosférickému tlaku mezi vodiči, jejichž napětí přesáhlo určitou hodnotu.
[69] Údaje pro obrázek byly převzaty z publikovaného textu přednášky J. Francka při převzetí Nobelovy ceny za fyziku v roce 1925; viz sborník Nobel Lectures, Physics (1922-1941). Elsevier Publ. Comp., Amsterdam 1965.
[70] V české literatuře jsou experimenty Franckova-Hertzova typu podrobněji diskutovány ve starší učebnici E. V. Špolskij: Atomová fyzika I. SNTL, Praha 1953.
[71] Pro podrobnější studium, které vyžaduje znalosti kvantové machaniky, odkazujeme na klasickou monografii J. H. van Vleck: Theory of Electric and Magnetic Susceptibilities. Oxford Umiversity Press. Oxford 1932, v české literatuře na znamenitou monografii S. Krupička: Fyzika feritů a příbuzných magnetických kysličníků. Academia, Praha 1969.
[72] Výpočet je podrobně uveden například v knize R. Becker, F. Sauter: Theorie der Elektrizität, III. Band. B. G. Teubner, Stuttgart 1968.
[73] Kvalitativně lze proces disociace pochopit jako důsledek toho, že vzhledem k vyšší permitivitě rozpouštědla jsou elektrické přitažlivé síly mezi ionty opačného znamení menší než ve vzduchu. Existence disocivaných molekul je tudíž energeticky výhodná.
[74] V českém jazyce například učebnice J. Kvasnica: Statistická fyzika. Academia, Praha 1983.