Uvažujme částici o klidové hmotnosti m0 nesoucí náboj q, která se pohybuje ve vakuu v elektromagnetickém poli popsaném intenzitou elektrického pole E a magnetickou indukcí B . Obecnou pohybovou rovnici této částice snadno získáme dosadíme-li do pohybové rovnice (2.16) Lorentzovu sílu (3.56) . Rovnice má tvar
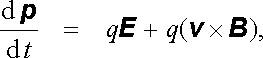 |
(6.1) |
kde je p hybnost částice a v její rychlost. Platí zcela obecně i pro vysoké rychlosti. V nerelativistickém přiblížení, kdy je rychlost v malá ve srovnání s rychlostí světla, místo (6.1) dostáváme
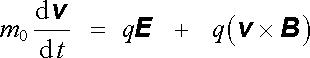 . . |
(6.2) |
Budeme-li polohu částice popisovat ve zvolené pravoúhlé soustavě souřadnic pomocí polohového vektoru r = r (x , y, z), můžeme pohybovou rovnici vyjádřit jako jednu vektorovou diferenciální rovnici pro neznámou funkci r = r (t)
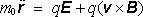 (6.3)
(6.3)
nebo (po rozepsání do složek) jako trojici diferenciálních rovnic pro neznámé složky polohového vektoru x = x(t), y = y(t), z = z( t)
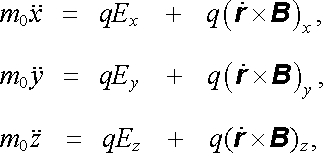 |
(6.3a) |
přičemž jsme, jak je v mechanice zvykem, tečkami nad příslušnými symboly označili časové derivace.
Z tvaru rovnic (6.2) až (6.3a) je patrná jejich důležitá vlastnost. V elektro-magnetickém poli libovolné prostorové a časové závislosti je pohyb částice určen jen jejím němým nábojem q /m0.
Užitím vztahu (3.56) pro Lorentzovu sílu lze snadno vypočítat práci, kterou elektromagnetické pole dodá pohybující se nabité částici. Během velmi krátkého časového intervalu dt se částice posune o d r = v dt a Lorentzova síla F vykoná práci F .d r = (F .v )dt . Jelikož platí (v ℜ × B ).v = 0, je vykonaná práce rovna q(v .E )dt . Okamžitý výkon dodávaný elektromagnetickým polem částici lze tedy vyjádřit jako q(v .E ). Předpokládáme-li dále, že v soustavě nenastávají žádné další přeměny energie, musí být dodaná práce spotřebována na zvýšení kinetické energie částice. Pro časovou změnu této kinetické energie dW k/dt tedy musí platit
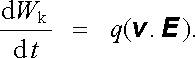 |
(6.4) |
Vztah (6.4) představuje obecné vyjádření zákona zachování energie pro vyšetřovanou soustavu. Musí tedy platit v každé situaci, například při libovolné, tj. i relativistické, rychlosti částice. Skutečnost, že časová změna kinetické energie částice nezávisí na magnetickém poli nepřekvapí; s podobnou situací jsme se již setkali v článku 5.2.1 při vyšetřování Poyntingovy věty.
Obecná pohybová rovnice (6.1) spolu s rovnicí (6.4) dovolují jednoduše vyjádřit vztah mezi změnou kinetické energie a časovou změnou hybnosti částice. Vynásobíme-li pohybovou rovnici (6.1) skalárně rychlostí v a uvědomíme-li si opět, že (v ℜ × B ).v = 0, dostaneme
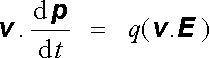 |
a po dosazení z (6.4) získáme výsledek
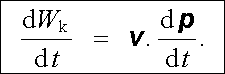 |
(6.5) |
Z hlediska Newtonovy formulace klasické mechaniky jsou mechanické účinky elektro-magnetického pole v plné obecnosti vyjádřeny Lorentzovou silou a pohybová rovnice (6.1) popisuje zcela obecně mechanické účinky elektromagnetického pole na nabitou částici. Její důsledky jsou v rámci nekvantové mechaniky v plné shodě s veškerou experimentální zkušeností. Poněkud jiný pohled na uvedený problém poskytuje analytická mechanika, v níž pojem síly není primárním pojmem.
Existuje několik možných způsobů formulace zákonů mechaniky bez použití pojmu síly. Pro speciální případ pohybu volné nabité částice v elektromagnetickém poli ukážeme postup využívající tzv. Lagrangeovy rovnice II. druhu, které budeme formulovat v kartézských souřadnicích.
Zmíněné Lagrangeovy rovnice jsou diferenciální rovnice, kterým musí vyhovovat tzv. Lagrangeova funkce L. Pro volnou částici studovanou v kartézských souřadnicích r ℜ ≡ (x1, x2, x3) mají tvar (viz. např. [12, 15])
 (6.6)
(6.6)
kde
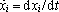 a i
= 1, 2, 3. Pro částici pohybující se v potenciálním poli je Lagrangeova
funkce rozdílem kinetické Wk a potenciální U(
r
,
t)
energie
částice; L = Wk - U(
r
,
t)
. Je-li
působení pole na částici závislé na její rychlosti, je nutné Lagrangeovu funkci
vyjádřit pomocí zobecněné potenciální funkce
a i
= 1, 2, 3. Pro částici pohybující se v potenciálním poli je Lagrangeova
funkce rozdílem kinetické Wk a potenciální U(
r
,
t)
energie
částice; L = Wk - U(
r
,
t)
. Je-li
působení pole na částici závislé na její rychlosti, je nutné Lagrangeovu funkci
vyjádřit pomocí zobecněné potenciální funkce
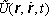 závislé na rychlosti. Tedy
závislé na rychlosti. Tedy
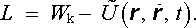 |
(6.7) |
Lagrangeova funkce částice v elektromagnetickém poli může být jednoduše vyjádřena pomocí elektromagnetických potenciálů φ ( r , t), A ( r , t) . V nerelativistickém přiblížení, tj. při malých rychlostech, platí (viz např. [15])
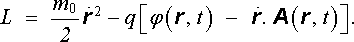 |
(6.8) |
Ukážeme, že z Lagrangeových rovnic (6.6) vyplývá pro Lagrangeovu funkci (6.8) pohybová rovnice (6.2) . Platí totiž
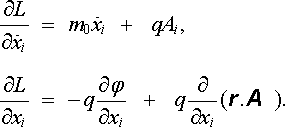 |
Uvědomíme-li si dále, že derivaci podle souřadnic provádíme při
konstantní rychlosti
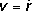 a použijeme-li (D 1.53), dostaneme
a použijeme-li (D 1.53), dostaneme
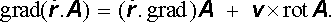 |
Jelikož totální derivaci vektorového potenciálu A ( r , t) podle času lze vyjádřit ve tvaru
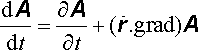 , , |
obdržíme po dosazení do (6.6) vektorovou rovnici
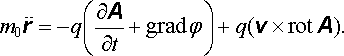 |
(6.9) |
První člen na pravé straně však je podle (5.28) roven qE a rot A = B , čímž již dostáváme pohybovou rovnici (6.2) .
Důležitou veličinou
v analytické mechanice je tzv. zobecněná
hybnost
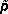 ,
jejíž jednotlivé složky jsou definovány vztahy
,
jejíž jednotlivé složky jsou definovány vztahy
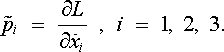 |
(6.10) |
Za předpokladu Lagrangeovy funkce tvaru (6.8) dostáváme pro zobecněnou hybnost
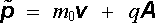 . . |
(6.11) |
Kinetická energie částice Wk = (m0v 2)/2 pak může být pomocí zobecněné hybnosti vyjádřena vztahem
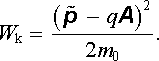 |
(6.12) |
Veličina
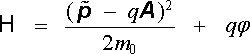 |
(6.13) |
vyjadřuje celkovou energii částice v elektromagnetickém poli a nazývá se Hamiltonovou funkcí. Uplatňuje se při popisu chování mikročástic v elektromagnetickém poli pomocí tzv. Hamiltonovych kanonických rovnic (viz opět [15]) a má značný význam pro formulaci kvantově mechanických rovnic vyjadřujících chování nabitých částic v elektromagnetickém poli.
Z dosud provedených úvah jsme viděli, že mechanické účinky elektromagnetického pole na nabitou částici mohou být popsány buď pohybovou rovnicí (6.1) , respektive (6.2) , nebo například Lagrangeovými rovnicemi pro Lagrangeovu funkci L. V prvním případě je elektromagnetické pole popisováno vektory E a B , ve druhém případě elektromagnetickými potenciály φ , A . V rámci nekvantové fyziky jsou oba popisy fyzikálně zcela ekvivalentní. Jak bylo již uvedeno v článku 3.3.3 při výkladu vlastností vektorového potenciálu stacionárního magnetického pole, nemění na uvedeném závěru nic ani skutečnost, že elektromagnetické potenciály nejsou určeny jednoznačně. Je ovšem nutné si uvědomit, že přímý fyzikální smysl nemohou mít vzhledem k této nejednoznačnosti samotné hodnoty potenciálů, ale jen veličiny kalibračně invariantní (srov. či. 5.1.4), které však mohou být pomocí potenciálů vyjádřeny.
Uvedená ekvivalence popisu přestane platit v kvantové mechanice, která ve srovnání s mechanikou klasickou představuje obecnější teorii. Stav částice je v kvantové mechanice popsán (obecně komplexní) vlnovou funkcí, která je vedle své amplitudy charakterizována i fází. Pohybové rovnice klasické mechaniky můžeme chápat jako limitní rovnice pro střední hodnoty kvantově mechanických veličin, ve kterých je informace o fázi vlnové funkce vystředována. Fáze vlnové funkce je však důležitá při studiu jevů mikrosvěta, v nichž se uplatňuje vlnový charakter pohybu částic. Jedním z takových důležitých jevů je interference.
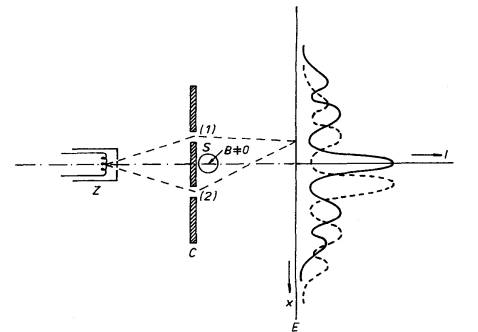
Obr. 6.1 K výkladu Bohmova-Aharonovova jevu.
Podstatné přitom je, že fáze vlnové funkce částice může být ovlivněna vektorovým potenciálem i v té části prostoru, v níž je magnetická indukce nulová. Jinými slovy řečeno, interakce mikročástice s elektromagnetickým polem nemůže být z hlediska kvantové mechaniky redukována jen na silové účinky popsané Lorentzovou silou (3.56) . V tomto smyslu má skutečnost, že kvantově mechanické rovnice vycházejí z Hamiltonovy funkce vyjádřené elektromagnetickými potenciály, hlubší fyzikální význam.
Jedním z konkrétních projevů uvedených souvislostí je tzv. Bohmův-Aharonovův jev, který spočívá ve sledování interference elektronů po průchodu dvěma štěrbinami (l) a (2), za kterými je umístěn velmi dlouhý solenoid S (viz obr. 6.1). Podstatou jevu je, že interferenční obrazec, pozorovaný na stínítku E, je závislý na tom, teče-li vinutím solenoidu proud, i když se elektrony pohybují "jen" v prostoru s nulovou magnetickou indukcí, avšak s nenulovým vektorovým potenciálem (srov. příklad 3.3.5e).[42]
Nakonec bychom chtěli ještě upozornit, že podobnost mezi experimentálním uspořádáním pro studium Bohmova-Aharonovova jevu a pro pozorování elektromagnetické indukce ve smyčce obklopující velmi dlouhý solenoid (viz. příklad 4.1.2c) je jen formální a nemá hlubší fyzikální souvislost. Na rozdíl od Bohmova-Aharonovova jevu je elektromagnetická indukce v uvedeném uspořádání plně popsatelná klasickými rovnicemi elektromagnetického pole, a to ekvivalentně buď pomocí vektorového potenciálu (srov. č1. 5.1.1), nebo například pomocí obecných rovnic elektromagnetického pole v integrálním tvaru (5.12) , v nichž vystupují jen vektory intenzit E , H a indukcí D , B .
Pro časově neproměnná homogenní pole lze pohybovou rovnici jednoduše integrovat. Probereme postupně několik takových situací.
Omezíme se na nerelativistický případ. Má-li pak částice na počátku působení elektrického pole polohu r 0 a rychlost v 0, lze postupnou integrací rovnice (6.3) vyjádřit obecnou časovou závislost rychlosti v (t) a polohy r (t) částice. Platí
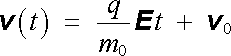 , , |
(6.14) |
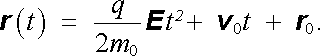 |
(6.15) |
Speciálně, je-li intenzita elektrického pole orientována ve směru počáteční rychlosti, je pohyb částice přímočarý a částice je rovnoměrně urychlována (či zpomalována) se zrychlením qE /m0. Je-li naopak počáteční rychlost v 0 kolmá k E , snadno se z (6.15) přesvědčíme, že dráhou částice je parabola.
V obecném případě libovolné rychlosti lze pohybovou rovnici (6.1) jednoduše integrovat, položíme-li směr jedné osy soustavy souřadné do směru intenzity elektrického pole. Použitím relativistických vztahů (2.17) až (2.20) lze jednoduše vyjádřit časovou závislost rychlosti částice. Pro rovnoběžnou orientaci počáteční rychlosti a intenzity pole je tento problém řešen v úloze Ú 6.1.
Magnetické pole nechť je orientováno ve směru osy z. Uvažme nejdříve speciální situaci, kdy počáteční rychlost částice v 0, mnohem menší než rychlost světla c, je kolmá ke směru z, tj. leží v rovině x y. Lorentzova síla bude mít konstantní velikost q v 0B a bude stále kolmá ke směru rychlosti. Magnetické pole nebude tedy podle (6.2) měnit velikost rychlosti částice, ale bude její dráhu zakřivovat konstantním dostředivým zrychlením a = (qv 0B)/m0. Částice tedy bude konat rovnoměrný kruhový pohyb v rovině x y s úhlovou frekvencí
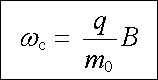 |
(6.16) |
nazývanou cyklotronová frekvence. Poloměr kružnice R0, po které se částice bude pohybovat, tzv. cyklotronový poloměr, je zřejmě dán vztahem
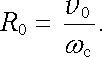 |
(6.17) |
V případě libovolné orientace počáteční rychlosti v 0 bude Lorentzova síla F dána jen složkou v 0,⊥ do roviny x y kolmé ke směru magnetického pole; F = v 0,⊥ B. Částice tedy bude v rovině x y konat rovnoměrný kruhový pohyb se stejnou cyklotronovou frekvencí ω c a poloměrem
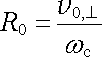 |
(6.18) |
a současně rovnoměrný přímočarý pohyb ve směru osy z s rychlostí v 0,|| . Výsledkem bude pohyb po šroubovici (viz obr. 6.2).


Právě vyšetřený charakter pohybu zůstane zachován i při velkých rychlo-stech. Skutečně, jelikož magnetické pole nemůže měnit velikost hybnosti částice, ale jen její směr, faktor
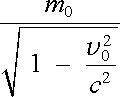 , , |
(6.19) |
který závisí jen na čtverci rychlosti, a tedy jen na velikosti hybnosti, bude zachovávat svoji hodnotu po celou dobu pohybu. Mezi časovou změnou hybnosti a časovou změnou rychlosti tedy bude platit vztah (srov. čl. 2.1.3)
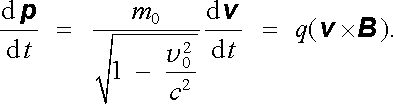 |
(6.20) |
Pohybová rovnice při velkých rychlostech se tedy liší jen faktorem (6.19) , kterým musí být rovněž korigována cyklotronová frekvence ω c. Dostáváme pro ni místo (6.16)
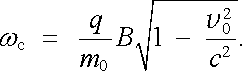 |
(6.21) |
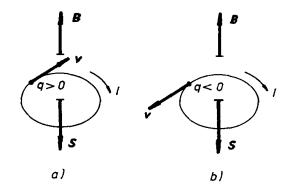
Je zajímavé, a i důležité, si všimnout směru rotace nabité částice. Z výrazu pro Lorentzovu sílu je možné se přesvědčit, že nezávisle na znamení náboje q částice rotuje v takovém smyslu, že orientujeme-li plochu S opisované smyčky podle pravidla pravotočivého šroubu vzhledem ke směru proudu I reprezentovaného částicí (viz obr. 6.3), bude směr vektoru S mířit proti směru magnetického pole B . Opačně vůči směru magnetického pole tedy bude orientován i vektor magnetického momentu m = IS , který rotující částici reprezentuje.
V tomto odstavci vyšetříme pohyb nabité částice (v nerelativistickém přiblížení) za současného působení homogenního elektrického pole E ℜ ≡ (0, E, 0) a ho-mogenního magnetického pole B ℜ ≡ (0, 0, B). Po dosazení speciálního tvaru pole do pohybové rovnice (6.3a) dostaneme
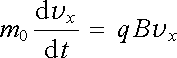 , , |
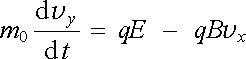 , , |
(6.22) |
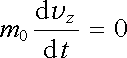 . . |
Za předpokladu, že počáteční rychlost v 0 bude mít nulovou složku do směru osy z, bude se pohyb částice odehrávat pouze v rovině x y. Budeme uvažovat tuto speciální situaci. Pohyb je pak zcela popsán prvními dvěma rovnicemi (6.22) a analýza jejich řešení může být zjednodušena zavedením komplexní rychlosti u = v x + i v y, neboť obě rovnice přejdou v jedinou komplexní pohybovou rovnici
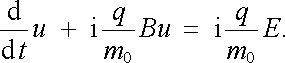 |
(6.23) |
Jde o nehomogenní lineární diferenciální rovnici, jejíž obecné řešení získáme jako součet obecného řešení příslušné homogenní rovnice a libovolného partikulárního řešení celé rovnice (6.23) . Obecné řešení homogenní rovnice hledáme ve tvaru
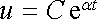 . . |
(6.24) |
Po dosazení do rovnice dostaneme pro konstantu
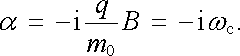 |
(6.25) |
Triviálním partikulárním řešením rovnice
(6.23)
je
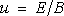 ,
takže obecné řešení může být zapsáno ve tvaru
,
takže obecné řešení může být zapsáno ve tvaru
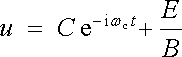 , , |
(6.26) |
kde C je obecně komplexní konstanta. Lze ji vyjádřit pomocí reálných konstant D, δ ve tvaru C = D exp(iδ ) a výsledek má pak tvar
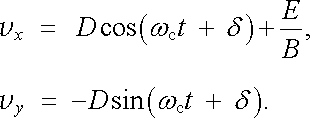 |
(6.27) |
Dále vyšetříme konkrétní průběh dráhy pro speciální tvar počátečních podmínek, kdy v čase t = 0 je částice v počátku s nulovou rychlostí, tj. platí x0 = y0 = z0 a v x,0 = v y,0 = 0. Z rovnic (6.27) pak plyne
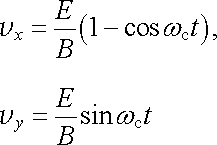 |
(6.28a) |
a po další integraci a uplatnění počátečních podmínek dostaneme pro časovou závislost souřadnic
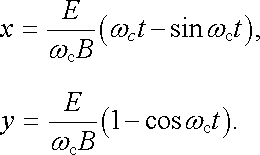 |
(6.28b) |
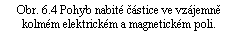


Obr.6.5 Dráha nabité částice ve vzájemně kolmém elektrickém a magnetickém poli při nenulové počáteční rychlosti: a) zkrácená cykloida, b) prodloužená cykloida.
Výrazy (6.28b) představují parametrické vyjádření cykloidy. Za uvedených počátečních podmínek je tedy dráhou částice obyčejná cykloida (viz obr. 6.4). Je-li počáteční rychlost v rovině x y nenulová, může mít dráha tvar zkrácené či prodloužené cykloidy, jak kvalitativně zobrazují obrázky 6.5a a 6.5b.
Nezávisle na počátečních rychlostech v x,0, v y,0 je podle (6.27) střední hodnota rychlosti v D ve směru osy x, tj. ve směru kolmém k E , rovna
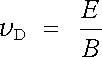 . . |
(6.29) |
Pozoruhodné je, že tato rychlost, nazývaná driftovou rychlostí, je nezávislá na znamení náboje částice.
Výsledky získané v odstavci 6.1.3b mohou být použity i v případě nehomogenního magnetického pole, pokud nehomogenita není příliš veliká. Pohyb si zachovává charakter šroubovice, její poloměr a stoupání však není obecně konstantní.
Uvažujeme osově symetrické magnetické pole, jehož osou symetrie je osa z (viz obr. 6.6). Díky osové symetrii je zřejmé, že pole má nenulovou jen podélnou složku Bz a radiální složku Br. Pohybuje-li se částice po šroubovici s pro-měnným stoupáním i poloměrem, má nenulovou podélnou složku rychlosti v z = dz/dt , radiální složku v r = dr/dt a samozřejmě i cirkulační složku v φ = rd φ /dt . Cirkulační pohyb částice je možné popsat pomocí druhé impulsové věty. Pro časovou změnu složky z momentu hybnosti Lz = m0ω r 2 musí tedy platit rovnice
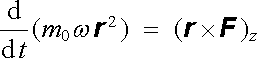 , , |
(6.30) |
kterou je možné, po zavedení radiální složky rychlosti v r = v xcosφ + v ysinφ a magnetické indukce Br = Bxcosφ + Bysinφ , vyjádřit ve tvaru
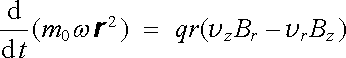 . . |
(6.31) |
Pozoruhodné je, že pravou stranou poslední rovnice lze vyjádřit pomocí magnetického toku Φ tekoucího plochou ohraničenou dráhou částice. Je možné se o tom snadno přesvědčit, vyjádříme-li magnetický tok Φ pomocí vektorového potenciálu vztahem typu (3.59a) . V našem případě osově symetrického pole je cirkulační složka vektorového potenciálu Aφ , nezávislá na úhlu φ , takže platí [43]
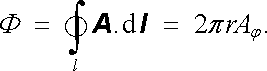 |
(6.32) |
Složky magnetické indukce Bz, Br na pravé straně (6.31) lze rovněž vyjádřit pomocí vektorového potenciálu. Díky osové symetrii pole je možné z obecných vzorců pro operaci rotace ve válcových souřadnicích získat
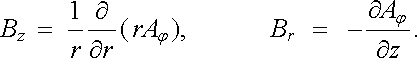 |
(6.33) |
Po dosazení do (6.31) pak využitím (6.32) dostaneme
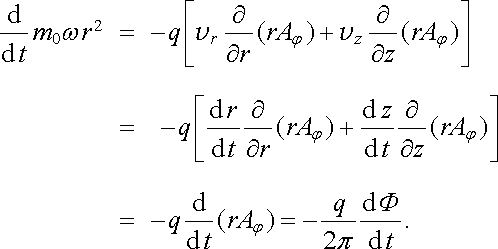 |
(6.34) |


Výsledek ukazuje, že časová změna součtu momentu hybnosti částice a magnetického toku vymezeného její dráhou je nulová. Hodnota této veličiny zůstává tedy při pohybu částice konstantní.