ElektronickĂŠ obvody, kterĂŠ realizujĂ logickĂŠ funkce dÄlĂme do zĂĄkladnĂch dvou skupin: na tzv. kombinaÄnĂ a sekvenÄnĂ logickĂŠ systĂŠmy. PrvnĂ skupina (logickĂĄ hradla) je charakterizovĂĄna tĂm, Ĺže vĂ˝stupnĂ stav systĂŠmu zĂĄvisĂ pouze na okamĹžitĂ˝ch stavech (kombinaci) vstupnĂch logickĂ˝ch promÄnnĂ˝ch; pĹi jejich zmÄnÄ dochĂĄzĂ ke zmÄnÄ vĂ˝stupnĂho stavu se zpoĹždÄnĂm, danĂŠm jen dobou prĹŻchodu signĂĄlu pĹes pouĹžitĂŠ elektronickĂŠ obvody. SekvenÄnĂ logickĂŠ systĂŠmy (systĂŠmy s mezipamÄtĂ, klopnĂŠ obvody) generujĂ vĂ˝stupnĂ stav na zĂĄkladÄ hodnoty vstupnĂch logickĂ˝ch promÄnnĂ˝ch a na zĂĄkladÄ pĹedchozĂ hodnoty vĂ˝stupu. VĂ˝stup tÄchto obvodĹŻ je tedy definovĂĄn jen tehdy, je-li definovĂĄna ÄasovĂĄ posloupnost (sekvence) zmÄn vstupnĂch hodnot; z toho tĂŠĹž plyne jejich nĂĄzev. Probereme nejprve pĹĂklady kombinaÄnĂch a pak sekvenÄnĂch logickĂ˝ch systĂŠmĹŻ.
Kombinujeme-li hradla OR a AND, popsanĂĄ v pĹedchĂĄzejĂcĂm odstavci, s invertorem, mĹŻĹžeme vytvoĹit celou Ĺadu dalĹĄĂch logickĂ˝ch funkcĂ, z nichĹž nejpouĹžĂvanÄjĹĄĂ jsou NAND - tzv. Shefferova funkce a NOR - tzv. Pierceova funkce. VytvoĹĂ se tak, Ĺže na vĂ˝stup hradla AND event. OR pĹipojĂme invertor. VĂ˝slednĂŠ pravdivostnĂ tabulky pak jsou:
NAND NOR
| X | Y | |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| X | X | |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Podle de MorganovĂ˝ch zĂĄkonĹŻ bychom mohli vytvoĹit hradlo NAND pĹipojenĂm dvou invertorĹŻ na oba vstupy hradla OR:
![]()
ObdobnÄ hradlo NOR lze vytvoĹit z hradla AND a dvou invertorĹŻ na vstupech:
![]()
Funkce NAND a NOR lze rozĹĄĂĹit na libovolnĂ˝ poÄet vstupnĂch logickĂ˝ch promÄnnĂ˝ch. Definice tÄchto funkcĂ si ÄtenĂĄĹ jistÄ snadno utvoĹĂ sĂĄm.
VĹĄimneme si jeĹĄtÄ tĹĂ sloĹženĂ˝ch logickĂ˝ch funkcĂ, kterĂŠ pro svou dĹŻleĹžitost jsou Äasto realizovĂĄny jako jeden logickĂ˝ Älen. Jsou to funkce EXCLUSIVE-OR nazĂ˝vanĂĄ tĂŠĹž neekvivalence, funkce EXCLUSIVE-NOR neboli ekvivalence, shodnost a funkce ÄtyĹ logickĂ˝ch promÄnnĂ˝ch AND - NOR, zvanĂĄ takĂŠ AND - OR - INVERT.
Funkci EXCLUSIVE - OR lze obecnÄ definovat pro n logickĂ˝ch promÄnnĂ˝ch. Tato funkce nabĂ˝vĂĄ hodnoty 1 prĂĄvÄ kdyĹž existuje mezi n vstupnĂmi logickĂ˝mi promÄnnĂ˝mi alespoĹ jedna, kterĂĄ mĂĄ jinou hodnotu, neĹž ostatnĂ. Lze snadno dokĂĄzat (dĹŻkaz je pĹenechĂĄn ÄtenĂĄĹi), Ĺže vyjĂĄdĹena v BooleovÄ algebĹe bude funkce EXCLUSIVE - OR mĂt tvar (A1,A2, ..., An jsou vstupnĂ logickĂŠ promÄnnĂŠ):
![]()
Zde jsme si rovnÄĹž zavedli znaÄku pro oznaÄenĂ tĂŠto logickĂŠ funkce. Aby nedoĹĄlo k zĂĄmÄnÄ se znaÄkou logickĂŠho souÄtu, budeme v tÄchto skriptech uĹžĂvat pro logickĂ˝ souÄet a souÄin pouze znaÄek â +â a â .â.
NynĂ si podrobnÄji rozebereme hradlo EXCLUSIVE-OR pro dvÄ vstupnĂ logickĂŠ promÄnnĂŠ. Je zĹejmĂŠ, Ĺže rozĹĄĂĹenĂ pro vĂce logickĂ˝ch promÄnnĂ˝ch by ĹĄlo provĂŠst napĹ. tĂmto zpĹŻsobem:
![]()
neboĹĽ existuje-li alespoĹ
jedna promÄnnĂĄ Ai pro kterou platĂ ![]() pro i = 1, 2, 3, ..., n-1, je souÄet na
pravĂŠ stranÄ tohoto vĂ˝razu roven logickĂŠ 1 nezĂĄvisle na
hodnotĂĄch ostatnĂch sÄĂtancĹŻ. MĹŻĹžeme tedy vytvoĹit funkci
EXCLUSIVE-OR pro n promÄnnĂ˝ch pomocĂ hradel realizujĂcĂch
tuto funkci pro dvÄ logickĂŠ promÄnnĂŠ a hradel zĂĄkladnĂch.
Jsou-li A, B vstupnĂ logickĂŠ promÄnnĂŠ, lze tuto funkci zapsat
jako
pro i = 1, 2, 3, ..., n-1, je souÄet na
pravĂŠ stranÄ tohoto vĂ˝razu roven logickĂŠ 1 nezĂĄvisle na
hodnotĂĄch ostatnĂch sÄĂtancĹŻ. MĹŻĹžeme tedy vytvoĹit funkci
EXCLUSIVE-OR pro n promÄnnĂ˝ch pomocĂ hradel realizujĂcĂch
tuto funkci pro dvÄ logickĂŠ promÄnnĂŠ a hradel zĂĄkladnĂch.
Jsou-li A, B vstupnĂ logickĂŠ promÄnnĂŠ, lze tuto funkci zapsat
jako ![]()
ÄtenĂĄĹ si jistÄ druhou rovnost snadno ovÄĹĂ. Z poslednĂho vztahu vyplĂ˝vĂĄ zapojenĂ hradla EXCLUSIVE-OR pomocĂ dvou hradel AND, dvou invertorĹŻ a hradla NOR - obr. 7.20. VĂ˝znam schematickĂ˝ch znaÄek je na obr.7.22.

| A | B | A Ě B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
DĹŻleĹžitost funkce EXCLUSIVE-OR vyplyne z nĂĄsledujĂcĂ Ăşvahy. ChtÄjme seÄĂst dvÄ binĂĄrnĂ ÄĂsla o jednom bitu. VĂ˝sledek nabude hodnoty 0 pakliĹže obÄ ÄĂsla budou 0 , hodnoty 1 je-li jedno z nich 0 a druhĂŠ 1. Jsou-li obÄ ÄĂsla rovna 1, pak souÄet bude opÄt 0, ale je potĹeba vytvoĹit pĹenos do eventuĂĄlnĂho nĂĄsledujĂcĂho bitu. OznaÄĂme-li souÄet S a pĹenos C (carry), pak je zĹejmĂŠ, Ĺže
S = A Ě B
C = A . B
Obvodu generujĂcĂmu tyto dvÄ veliÄiny se ĹĂkĂĄ polosÄĂtaÄka a nĂĄleĹžitĂĄ pozornost mu bude vÄnovĂĄna pozdÄji. Na obr. 7.20 je rovnÄĹž znĂĄzornÄno, Ĺže jednoduchou Ăşpravou (vyvedenĂm jednoho ze vstupĹŻ hradla NOR) lze zĂskat z hradla EXCLUSIVE-OR polosÄĂtaÄku.
Ekvivalence je jak jiĹž nĂĄzev napovĂdĂĄ inverznĂ funkcĂ k prĂĄvÄ popsanĂŠ a lze ji jednoduĹĄe vytvoĹit pĹidĂĄnĂm invertoru k hradlu EXCLUSIVE-OR. Tohoto zpĹŻsobu vĹĄak nenĂ moĹžno pouĹžĂt pĹi nĂĄvrhu sloĹžitÄjĹĄĂch logickĂ˝ch sĂtĂ a vĹždy je nutno promyslet nejefektivnÄjĹĄĂ zpĹŻsob generace tĂŠ kterĂŠ logickĂŠ funkce, jinak by neĂşmÄrnÄ narĹŻstaly rozmÄry, pĹĂkon a ve zdaleka ne poslednĂ ĹadÄ takĂŠ cena pĹĂsluĹĄnĂŠ logickĂŠ sĂtÄ. Proto vztah pro tuto funkci upravĂme:
![]()
Lze tedy snadno upravit schĂŠma na obr. 7.20. buÄ uĹžitĂm na vĂ˝stupu hradla OR mĂsto hradla NOR, nebo prostou zmÄnou zapojenĂ vstupĹŻ hradel AND jak je ukĂĄzĂĄno na obr. 7.21. Toto zapojenĂ je vĂ˝hodnĂŠ zejmĂŠna tĂm, Ĺže vyvedenĂm vĂ˝stupĹŻ hradel
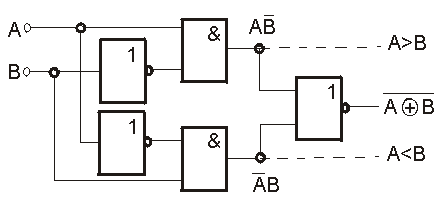
| A | B | |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
AND zĂskĂĄme jednobitovĂ˝
komparĂĄtor. SouÄin ![]() je totiĹž
roven 1 prĂĄvÄ kdyĹž A = 1 a B = 0 tj.A > B, stejnÄ
je totiĹž
roven 1 prĂĄvÄ kdyĹž A = 1 a B = 0 tj.A > B, stejnÄ ![]() je rovno 1 prĂĄvÄ kdyĹž A = 1 a B = 0,
tj. A < B. Výstup
je rovno 1 prĂĄvÄ kdyĹž A = 1 a B = 0,
tj. A < B. VĂ˝stup ![]() je roven 1 prĂĄvÄ kdyĹž
AÂ =Â B =Â 0 nebo AÂ =Â BÂ =Â 1.
je roven 1 prĂĄvÄ kdyĹž
AÂ =Â B =Â 0 nebo AÂ =Â BÂ =Â 1.
Hradla AND-OR-INVERT jsou logickÊ obvody sestavenÊ ze dvou hradel AND a z jednoho hradla NOR. Pravdivostnà tabulka takovÊho hradla je uvedena vlevo, schÊma je na obr.7.23.
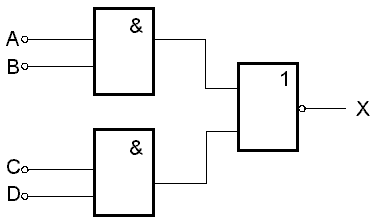
| A | B | C | D | X |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 |
VyjĂĄdĹenĂ logickĂŠ funkce je jednoduchĂŠ. Je to:
![]()
ProÄ se tyto obvody vyrĂĄbÄly v integrovanĂŠ formÄ vyplyne nejlĂŠpe, porovnĂĄme-li obrĂĄzek 7.23 s obr. 7.20 a 7.21. Z tohoto srovnĂĄnĂ vidĂme, Ĺže mĹŻĹžeme tĂmto obvodem za pomoci dvou invertorĹŻ vytvoĹit funkce EXCLUSIVE-OR/NOR a navĂc propojĂme-li oba vstupy kaĹždĂŠho u hradel AND, mĹŻĹžeme realizovat funkci NOR. Tato hradla se vyrĂĄbÄla pod oznaÄenĂm 7450 a 7453.
DĹŻleĹžitĂ˝mi kombinaÄnĂmi logickĂ˝mi obvody jsou dekodĂŠry, kterĂŠ slouŞà k pĹevodu informace vyjĂĄdĹenĂŠ v jednom kĂłdu na jinĂ˝. Jako pĹĂklad si zde uvedeme dekodĂŠr 1/N, kterĂ˝ pĹevĂĄdĂ slovo z binĂĄrnĂho kĂłdu na kĂłd N promÄnnĂ˝ch, kde kaĹždĂĄ promÄnnĂĄ je vedena po samostatnĂŠm vodiÄi. PrincipiĂĄlnĂ zapojenĂ pro N = 4 je uvedeno na obr. 7.24 spolu s pravdivostnĂ tabulkou.
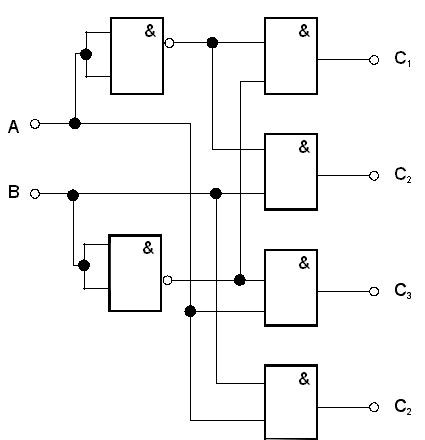
| vstupy | výstupy | ||||
| A | B | C1 | C2 | C3 | C4 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
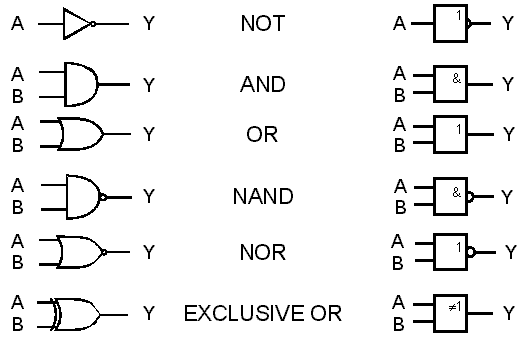
SchematickĂŠ znaÄky logickĂ˝ch obvodĹŻ jsou uvedeny na obr. 7.22. Na levĂŠ stranÄ jsou uvedeny znaÄky starĹĄĂ, jeĹĄtÄ vĹĄak hojnÄ pouĹžĂvanĂŠ, na pravĂŠ novÄjĹĄĂ, pĹizpĹŻsobenĂŠ ke snadnÄjĂmu grafickĂŠmu znĂĄzornÄnĂ.