ObjektĹŻ, kterĂŠ nabĂ˝vajĂ pouze dvou opaÄnĂ˝ch stavĹŻ existuje v praxi celĂĄ Ĺada a nÄkterĂŠ z nich byly vyjmenovĂĄny v pĹedchozĂm odstavci.
Velice snadno si lze pĹedstavit situaci, kdy rozhodovĂĄnĂ o dalĹĄĂ Äinnosti resp. stavu objektu zĂĄvisĂ na stavech nÄkolika takovĂ˝ch entit. MĂĄ-li tato dalĹĄĂ Äinnost resp. stav objektu rovnÄĹž charakter dvoustavovĂŠ entity, pak se poÄet moĹžnĂ˝ch kombinacĂ vstupnĂch tj. nezĂĄvislĂ˝ch parametrĹŻ (kterĂ˝ch je pĹi n vstupnĂch parametrech 2n) musĂ nutnÄ redukovat na 2 stavy vĂ˝stupnĂho objektu, napĹĂklad pĹi m kombinacĂch nabude vĂ˝stupnĂ objekt jednoho stavu a pĹi zbylĂ˝ch 2n - m stavu druhĂŠho. PotĹebujeme proto urÄitĂ˝ pĹedpis, podle kterĂŠho bychom byli schopni pĹiĹadit sobÄ odpovĂdajĂcĂ stavy vstupnĂch promÄnnĂ˝ch a stav vĂ˝stupnĂho objektu. TakovĂ˝ pĹedpis se nazĂ˝vĂĄ logickĂĄ funkce n promÄnnĂ˝ch. Proces rozhodovĂĄnĂ, tj. vĂ˝bÄru odpovĂdajĂcĂch si stavĹŻ nazĂ˝vĂĄme logickou operacĂ a dvoustavovĂŠ entity, se kterĂ˝mi pracujeme, logickĂŠ promÄnnĂŠ. Hodnoty resp. stavy, kterĂŠ logickĂŠ promÄnnĂŠ nabĂ˝vajĂ se oznaÄujĂ zpravidla 1 a 0 (logickĂĄ jedniÄka a logickĂĄ nula), pĹĂpadnÄ H a L (high and low, zejmĂŠna v popisech elektronickĂ˝ch schĂŠmat s logickĂ˝mi obvody) nebo takĂŠ T a F (true a false, zejmĂŠna v poÄĂtaÄovĂ˝ch programech).
IntuitivnÄ lze tuĹĄit, Ĺže sloĹžitÄjĹĄĂ logickĂŠ funkce bude moĹžnĂŠ realizovat kombinacĂ tÄch nejjednoduĹĄĹĄĂch, tj. tÄch, kterĂŠ pouĹžĂvajĂ pouze dvou vstupnĂch logickĂ˝ch promÄnnĂ˝ch. Z tÄchto logickĂ˝ch funkcĂ byly zvoleny dvÄ, kterĂŠ se pouĹžĂvajĂ pro reprezentaci vĹĄech ostatnĂch. TÄmito logickĂ˝mi funkcemi jsou tzv. logickĂ˝ souÄet a logickĂ˝ souÄin. LogickĂ˝ souÄet reprezentuje rozhodovĂĄnĂ typu NEBO a logickĂ˝ souÄin rozhodovĂĄnĂ typu A . Pro pĹĂpad dvou logickĂ˝ch promÄnnĂ˝ch platĂ v pĹĂpadÄ NEBO nĂĄsledujĂcĂ pravdivostnĂ tabulka:
| A | B | A + B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Jak uvedeno v tabulce, uĹžĂvĂĄ se pro oznaÄenĂ logickĂŠho souÄtu obvykle stejnĂŠho symbolu jako pro souÄet algebraickĂ˝. Lze se vĹĄak setkat i s jinĂ˝mi symboly (napĹĂklad A Ă B atd.). Z tabulky je vidÄt, Ĺže pro to, aby vĂ˝sledek logickĂŠho souÄtu nabyl hodnoty 1 staÄĂ, aby alespoĹ jedna z logickĂ˝ch promÄnnĂ˝ch nabyla hodnoty 1. MajĂ-li napĹ. dvÄ nebo vĂce logickĂ˝ch promÄnnĂ˝ch tvoĹĂcĂch logickĂ˝ souÄet hodnotu 1, nemĹŻĹže ovĹĄem tento nabĂ˝ti jinĂŠ hodnoty neĹž 1, neboĹĽ vĂ˝sledek logickĂŠho souÄtu je rovnÄĹž dvoustavovĂĄ promÄnnĂĄ.
Pro logickĂ˝ souÄin platĂ nĂĄsledujĂcĂ pravdivostnĂ tabulka:
| A | B | A . B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Pro logickĂ˝ souÄin budeme uĹžĂvat oznaÄenĂ A.B event. AB; jinĂŠ symboly napĹ. A ĹŽ B se uĹžĂvajĂ mĂĄlo. Aby tedy vĂ˝sledek logickĂŠho souÄinu nabyl logickĂŠ hodnoty 1, je nutnĂŠ, aby vĹĄechny logickĂŠ promÄnnĂŠ, tvoĹĂcĂ tento souÄin nabyly hodnoty 1, jinak nabĂ˝vĂĄ vĂ˝sledek hodnoty 0.
KromÄ tÄchto dvou operacĂ pro logickĂŠ funkce dvou promÄnnĂ˝ch je tĹeba jeĹĄtÄ zavĂŠst logickou funkci jednĂŠ promÄnnĂŠ. Je vĂ˝hodnĂŠ zavĂŠst funkci negace, tj.funkci, kterĂĄ pĹiĹazuje logickĂŠ promÄnnĂŠ tu hodnotu, kterou nemĂĄ, tj. logickĂŠ nule jedniÄku a naopak. Pro logickou promÄnnou X je oznaÄenĂ negace X.
V nĂĄsledujĂcĂm odstavci si dokĂĄĹžeme, Ĺže dvojstavovĂŠ promÄnnĂŠ spolu s uvedenĂ˝mi operacemi tvoĹĂ tzv. Booleovu algebru.
V pĹedchĂĄzejĂcĂm odstavci jsme se zmĂnili, Ĺže mnoĹžina dvojstavovĂ˝ch promÄnnĂ˝ch spolu s operacemi logickĂŠho souÄtu, souÄinu a negace tvoĹĂ tzv. Booleovu algebru. Pojem Booleovy algebry je vĹĄak obecnÄjĹĄĂ, takĹže nĂĄmi uvedenĂĄ mnoĹžina je jen jejĂ speciĂĄlnĂ pĹĂpad. Vyvinul se v nĂĄvaznosti na analogii mezi mnoĹžinovĂ˝mi operacemi sjednocenĂ a prĹŻnik a aritmetickĂ˝mi operacemi sÄĂtĂĄnĂ a nĂĄsobenĂ. Rozsah a dĹŻleĹžitost tĂŠto analogie objasnil jako prvnĂ britskĂ˝ matematik George Boole (1815-1864), kterĂ˝ poloĹžil zĂĄklady algebraickĂŠ teorie mnoĹžin pĹed vĂce neĹž 100 lety.
ObecnÄ je Booleova algebra definovĂĄna takto:
Booleova algebra je mnoĹžina B prvkĹŻ a, b, c, ... s nĂĄsledujĂcĂmi vlastnostmi:
a) B mĂĄ dvÄ binĂĄrnĂ operace, ĹŽ (prĹŻnik) a Ă ( sjednocenĂ ), kterĂĄ jsou
idempotentnĂ a ĹŽ a = a Ă a = a
komutativnĂ a ĹŽ b = b ĹŽ a , a Ă b = b Ă a
asociativnĂ a ĹŽ (b ĹŽ c) = (a ĹŽ b) ĹŽ c
a Ă (b Ă c) = ( aĂ b) Ă c
b) tyto operace vyhovujĂ zĂĄkonĹŻm absorpce
a ĹŽ (b Ă b) = a Ă ( a ĹŽ b) = a
c) obÄ operace jsou distributivnĂ
a ĹŽ ( b Ă c) = ( a ĹŽ b ) Ă ( a ĹŽ c )
a Ă ( b ĹŽ c) = ( a Ă b) ĹŽ ( a Ă c )
d) obsahuje univerzĂĄlnĂ ohraniÄenĂ 0 a 1 , kterĂĄ vyhovujĂ vztahĹŻm
0 ĹŽ a = 0 , 0 Ă a = a ,
e) B mĂĄ unĂĄrnĂ operaci ![]()
tvoĹenĂ komplementu s vlastnostmi:
![]() a
a ![]()
DĂĄle lze z definice dokĂĄzat Ĺadu vlastnostĂ BooleovĂ˝ch algeber. Jsou to pĹedevĹĄĂm zobecnÄnĂŠ distributivnĂ zĂĄkony:
![]()
pro x, a1, a2 , ...., an Ă B
![]()
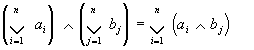
pro ai, bj , Ă B; i = 1, 2, ...., n; j = 1, 2, ...., m, kde
![]()
DĂĄle se dajĂ dokĂĄzat zobecnÄnĂŠ de Morganovy zĂĄkony
![]()
![]()
Pro dalĹĄĂ vĂ˝klad budeme potĹebovat nĂĄsledujĂcĂ
vÄtu. KaĹždĂ˝ BooleovskĂ˝ vĂ˝raz (tj. vĂ˝raz utvoĹenĂ˝ pomocĂ operacĂ " ĹŽ ", " Ă ",
" Äž ", ve
kterĂŠm se vyskytuje n prvkĹŻ x1, .., xn se dĂĄ vyjĂĄdĹit prĂĄvÄ jednĂm zpĹŻsobem jako sjednocenĂ
tzv. minimĂĄlnĂch booleovskĂ˝ch polynomĹŻ, tj. vĂ˝razĹŻ tvaru ![]() , kde buÄ ai = Xi:
nebo ai =
, kde buÄ ai = Xi:
nebo ai = ![]() . Tomuto tvaru BooleovskÊho výrazů (nebo BooleovskÊ funkce)
se ĹĂkĂĄ disjunktivnĂ kanonickĂ˝ tvar. MinimĂĄlnĂm booleovskĂ˝m polynomĹŻm se Äasto
ĹĂkĂĄ mintermy (z anglickĂŠho minimal polynomial term). DĹŻkaz tĂŠto vÄty nenĂ
sloĹžitĂ˝, avĹĄak vyboÄuje jiĹž z rĂĄmce tÄchto skript. ÄtenĂĄĹ jej mĹŻĹže najĂt
v bÄĹžnÄ dostupnĂŠ literatuĹe.
. Tomuto tvaru BooleovskÊho výrazů (nebo BooleovskÊ funkce)
se ĹĂkĂĄ disjunktivnĂ kanonickĂ˝ tvar. MinimĂĄlnĂm booleovskĂ˝m polynomĹŻm se Äasto
ĹĂkĂĄ mintermy (z anglickĂŠho minimal polynomial term). DĹŻkaz tĂŠto vÄty nenĂ
sloĹžitĂ˝, avĹĄak vyboÄuje jiĹž z rĂĄmce tÄchto skript. ÄtenĂĄĹ jej mĹŻĹže najĂt
v bÄĹžnÄ dostupnĂŠ literatuĹe.
DĂĄ se ukĂĄzat, Ĺže pro n promÄnnĂ˝ch X1,
..., Xn existuje 2n různých
minimĂĄlnĂch polynomĹŻ X1 X2 ...Xn, ![]() 1X2... Xn,
1X2... Xn, ![]() .
Z tÄchto polynomĹŻ pak mĹŻĹžeme utvoĹit celkem
.
Z tÄchto polynomĹŻ pak mĹŻĹžeme utvoĹit celkem ![]() kombinacĂ,
coĹž je takĂŠ celkovĂ˝ poÄet rĹŻznĂ˝ch booleovskĂ˝ch funkcĂ n promÄnnĂ˝ch, protoĹže
podle prĂĄvÄ uvedenĂŠ vÄty je vyjĂĄdĹenĂ v minimĂĄlnĂch polynomech
jednoznaÄnĂŠ.
kombinacĂ,
coĹž je takĂŠ celkovĂ˝ poÄet rĹŻznĂ˝ch booleovskĂ˝ch funkcĂ n promÄnnĂ˝ch, protoĹže
podle prĂĄvÄ uvedenĂŠ vÄty je vyjĂĄdĹenĂ v minimĂĄlnĂch polynomech
jednoznaÄnĂŠ.
Pro Ăşplnost je tĹeba jeĹĄtÄ uvĂŠst, Ĺže prĂĄvÄ tak, jako pomocĂ minimĂĄlnĂch
polynomĹŻ, se dĂĄ kaĹždĂĄ BooleovskĂĄ funkce vyjĂĄdĹit jednoznaÄnÄ jako prĹŻnik tzv.
maximĂĄlnĂch booleovskĂ˝ch polynomĹŻ (maxtermĹŻ), coĹž jsou vĂ˝razy tvaru ![]() ,kde opÄt buÄ ai=Xi
nebo ai =
,kde opÄt buÄ ai=Xi
nebo ai = ![]() .
.
ProtoĹže je vĹĄak zĹejmĂŠ, Ĺže lze pomocĂ de
MorganovĂ˝ch zĂĄkonĹŻ snadno pĹevĂĄdÄt tvar mintermovĂ˝ na tvar maxtermovĂ˝
(vyjĂĄdĹĂme-li nejprve inversi poĹžadovanĂŠ funkce F v jednom tvaru a pak
aplikujeme de MorganĹŻv zĂĄkon, abychom zĂskali ![]() tj. F), nenachĂĄzĂ maxtermovĂ˝ tvar tak ĹĄirokĂŠ vyuĹžitĂ jako
mintermovĂ˝.
tj. F), nenachĂĄzĂ maxtermovĂ˝ tvar tak ĹĄirokĂŠ vyuĹžitĂ jako
mintermovĂ˝.
Z definice Booleovy algebry plyne, Ĺže mnoĹžina dvoustavovĂ˝ch (logickĂ˝ch) promÄnnĂ˝ch tvoĹĂ Booleovu algebru. LogickĂ˝ souÄin je prĹŻnikem a logickĂ˝ souÄet sjednocenĂm kterĂŠ jsou:
1. komutativnĂ
(A + B) = (B + A)
(A . B) = (B . A)
2 .asociativnĂ
A + B + C = A + (B + C) = (A + B) + C
A .B .C = A .(B .C) = (A .B) .C
3. distributivnĂ
A .(B + C) = A .B + AC
A + (B .C) = (A + B) .(A + C)
UnĂĄrnĂ operace je tvoĹenĂ inverze : A ÂŽ ![]() vytvoĹĂ
negovanĂ˝ komplement logickĂŠ promÄnnĂŠ.
vytvoĹĂ
negovanĂ˝ komplement logickĂŠ promÄnnĂŠ.
T a b u l k a 5.2
| Funkce | NĂĄzev funkce | LogickĂ˝ Älen | AlgebraickĂ˝ vĂ˝raz |
| f0 | konstanta | 0 | |
| f1 | logickĂ˝ souÄet | NEBO(OR,ODER) | a + b |
| f2 | implikace | ||
| f3 | implikace | ||
| f4 | Shefferova funkce | NAND | |
| f5 | logickĂ˝ souÄin | A ( AND,UND) | ab |
| f6 | inhibice | ||
| f7 | inhibice | ||
| f8 | Pierceova funkce | NOR | |
| f9 | identita | a | |
| f10 | identita | b | |
| f11 | ekvivalence | ||
| f12 | neekvivalence | Exclusive OR | |
| f13 | negace | NE (NOT,NICHT) | |
| f14 | negace | NE (NOT,NICHT) | |
| f15 | konstanta | 1 |
PomocĂ zĂĄkladnĂch operacĂ logickĂŠho souÄtu souÄinu a negace mĹŻĹžeme pro jednu logickou promÄnnou vytvoĹit devÄt zĂĄkladnĂch identit:
1. A =
identita invert
2. A. 1 = A
3. A. 0 = 0 identity logickĂŠho souÄinu
4. A.A = A
5.
6. A+1 = 1
7. A+0 = A identity logickĂŠho souÄtu
8. A+A = A
9.
DĂĄle v BooleovÄ algebĹe logickĂ˝ch promÄnnĂ˝ch mĹŻĹžeme de Morganovy teorĂŠmy vyjĂĄdĹit pro dvÄ logickĂŠ promÄnnĂŠ ve tvaru:
![]()
![]()
UvedenĂ˝ch vztahĹŻ a identit mĹŻĹžeme vyuĹžĂt ke zjednoduĹĄenĂ sloĹžitÄjĹĄĂch logickĂ˝ch funkcĂ.
Jak bylo uvedeno v obecnĂŠ ÄĂĄsti z Booleovy algebry plyne, Ĺže dvÄma logickĂ˝mi promÄnnĂ˝mi lze realizovat celkem 24 = 16 funkcĂ, z nichĹž nÄkterĂ˝m se dostalo zvlĂĄĹĄtnĂho pojmenovĂĄnĂ. PĹehled tÄchto funkcĂ je uveden v tabulce 5.2.
MnoĹžina logickĂ˝ch operacĂ nenĂ ovĹĄem jedinĂĄ BooleovskĂĄ algebra. ÄtenĂĄĹ si mĹŻĹže snadno ovÄĹit, Ĺže napĹĂklad podmnoĹžiny urÄitĂŠ mnoĹžiny M, ve kterĂŠ je definovĂĄn prĹŻnik, sjednocenĂ a tvoĹenĂ komplementu zpĹŻsobem bÄĹžnĂ˝m pro tyto mnoĹžinovĂŠ operace, tvoĹĂ rovnÄĹž Booleovu algebru.
ObdobnÄ jako pĹi nĂĄvrhu
lineĂĄrnĂch obvodĹŻ je i ÄĂslicovĂ˝ obvod sloĹžen z Ĺady
blokĹŻ, z nichĹž kaĹždĂ˝ generuje specifickou logickou funkci.
TakovĂ˝ blok, kterĂ˝ vytvĂĄĹĂ sloĹžitÄjĹĄĂ logickou funkci
budeme nazĂ˝vat logickĂĄ sĂĹĽ a jednoduĹĄĹĄĂ logickĂ˝ obvod
reprezentujĂcĂ zpravidla logickou funkci dvou promÄnnĂ˝ch
budeme nazývat logickým
Älenem. Hranice mezi tÄmito dvÄma pojmenovĂĄnĂmi vĹĄak nenĂ
jednotnĂĄ, zejmĂŠna pĹi nĂĄvrhu sloĹžitÄjĹĄĂch logickĂ˝ch
sĂtĂ je tendence oznaÄovat logickĂ˝m Älenem i sloĹžitÄjĹĄĂ
logickĂ˝ obvod napĹ. vĂce neĹž dvou promÄnnĂ˝ch; v podstatÄ
se tohoto nĂĄzvu Äasto
uĹžĂvĂĄ pro integrovanĂ˝ obvod v jednom pouzdĹe. My se vĹĄak v
tÄchto skriptech pĹidrĹžĂme zavedenĂŠho pojmenovĂĄnĂ.
Jak plyne z Booleovy algebry, je moŞnÊ libovolnou logickou
funkci vyjĂĄdĹit kombinaci logickĂŠho souÄtu nebo logickĂŠho
souÄinu a operace negace. Chceme-li tedy sestrojit obvod,
kterĂ˝ by modeloval nÄjakou zadanou logickou funkci, musĂme
mĂt k dispozici obvody, kterĂŠ generujĂ uvedenĂŠ zĂĄkladnĂ
logickÊ funkce. ElektronickÊ obvody pro generaci uvedených
funkcĂ nazĂ˝vĂĄme po ĹadÄ: hradlo âORâ, hradlo âANDâ a invertor. Zde
se budeme zabĂ˝vat pouze nejjednoduĹĄĹĄĂmi obvody bez zĹetele
na event. zatĂĹžitelnost, rychlost apod. TakovĂ˝mi obvody je
tzv. diodovĂĄ logika DL- diode logic (pĹesnÄji ĹeÄeno
odporovÄ - diodovĂĄ logika). DĹĂve neĹž si rozebereme schĂŠmata, je tĹeba vysvÄtlit pojmy
tzv. pozitivnĂ a negativnĂ logiky. PĹiĹazenĂ logickĂ˝ch
stavĹŻ â0â a  â1â napÄĹĽovĂ˝m ĂşrovnĂm je totiĹž
zcela libovolnĂŠ a zĂĄleŞà na tom kterĂŠm pĹĂstroji, jakĂŠho
pĹiĹazenĂ pouĹžĂvĂĄ. PakliĹže stav logickĂŠ â0â
odpovĂdĂĄ niŞťĂmu napÄtĂ na vĂ˝stupu logickĂŠho Älenu
neĹžli stav logickĂŠ â1â, hovoĹĂme o tzv. pozitivnĂ
logice. Je-li tomu naopak, tj. logickĂŠ â0â odpovĂdĂĄ
vyĹĄĹĄĂ napÄtĂ neĹžli logickĂŠ â1â, pak se jednĂĄ
o negativnĂ logiku. PĹitom je tĹeba zdĹŻraznit, Ĺže
nezĂĄleŞà na velikosti napÄtĂ, obÄ mohou bĂ˝t kladnĂĄ nebo obÄ
zåpornå nebo jedno kladnÊ a druhÊ zåpornÊ; pakliŞe
logickĂĄ â1â odpovĂdĂĄ kladnÄjĹĄĂmu napÄtĂ, jednĂĄ se
o pozitivnĂ logiku, jinak je to logika negativnĂ. StejnĂ˝m
zpĹŻsobem se oznaÄuje logika tzv. dynamickĂĄ (na rozdĂl od
prĂĄvÄ popsanĂŠ
statickĂŠ, neboli ĂşrovĹovĂŠ logiky), kdy ovĹĄem pĹĂsluĹĄnĂŠ
ĂşrovnÄ jsou na vstupech logickĂ˝ch ÄlenĹŻ pouze po velmi
krĂĄtkou dobu, tedy ve formÄ napÄĹĽovĂ˝ch impulsĹŻ.
Vzhledem k tomu, Ĺže parametry reĂĄlnĂŠho logickĂŠho Älenu se
rĹŻznĂ kus od kusu (uĹžĂvajĂ se odpory s urÄitou tolerancĂ,
tranzistory a diody, kterĂŠ mohou mĂt rĹŻznĂŠ parametry), nenĂ
moĹžnĂŠ stanovit pĹesnou hodnotu napÄtĂ odpovĂdajĂcĂ
logickĂŠ â0â resp. â1â v tĂŠ kterĂŠ logickĂŠ sĂti.
MĂsto toho se logickĂŠ Äleny konstruujĂ tak, aby nebyly
citlivĂŠ na zmÄnu napÄtĂ
vstupnĂch parametrĹŻ pokud tyto leŞà v urÄitĂŠm intervalu
napÄtĂ. Viz obr.7.1.

NapĹĂklad pro hradla TTL (transistor-transistor-logic) jsou pĹĂsluĹĄnĂŠ intervaly nĂĄsledujĂcĂ:
Uvst(0) = max. 0,8 V
Uvst(1) = min. 2 V
neboli pro logickou â0â je povolenĂ˝ interval vstupnĂch napÄtĂ 0 - 0.8V pro logickou â1â 2 - 5 V. Hradlo samo mĂĄ zaruÄovanĂĄ vĂ˝stupnĂ napÄtĂ:
Uvýst(1) = min. 2,4 V
Uvýst(0) = max. 0,4 V
tj. hluboce v povolenĂŠ toleranci napÄtĂ vstupnĂch. NapĂĄjecĂ napÄtĂ je (5Âą 0,25) V. UvedenĂŠ hodnoty jsou typickĂŠ pro tzv. tranzistorovou logiku a byly implementovĂĄny u celĂŠ Ĺady vĂ˝robcĹŻ logickĂ˝ch obvodĹŻ. Zdaleka to vĹĄak nejsou jedinĂŠ napÄĹĽovĂŠ ĂşrovnÄ u logickĂ˝ch obvodĹŻ pouĹžĂvanĂŠ. Hradla s tranzistory ĹĂzenĂ˝mi elektrickĂ˝m polem majĂ logickĂŠ ĂşrovnÄ okolo 0 V a 9 V a existuje i tzv. logika s vysokou ĹĄumovou imunitou HLL (high-level-logic), kde napÄĹĽovĂĄ ĂşroveĹ logickĂŠ â1â je ĹĂĄdu 10 - 50 V. S takovĂ˝mi napÄĹĽovĂ˝mi logickĂ˝mi ĂşrovnÄmi pracujĂ ĹĂdicĂ systĂŠmy v provozech, kde je zvýťenĂĄ ĂşroveĹ elektromagnetickĂŠho ruĹĄenĂ. Na druhĂŠ stranÄ pro speciĂĄlnĂ pĹĂstroje s nĂzkĂ˝m napĂĄjecĂm napÄtĂm (nĂĄramkovĂŠ hodinky) byly vyvinuty obvody, kde jsou logickĂŠ ĂşrovnÄ mezi 0 V a 3 V i nĂĹže.
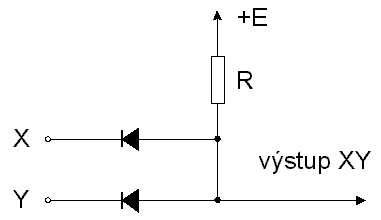
Pokud nebude vĂ˝slovnÄ uveden opak, budeme se v tÄchto skriptech zabĂ˝vat pouze pozitivnĂ logikou. PodĂvejme se nynĂ na elektronickou reprezentaci hradla typu OR na obr. 7.2. Jak jiĹž bylo uvedeno, hradlo tohoto typu je vybaveno (na jeho vĂ˝stupu je ĂşroveĹ logickĂŠ 1), je-li alespoĹ jeden z jeho vstupĹŻ vybaven.
| X | Y | X+Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
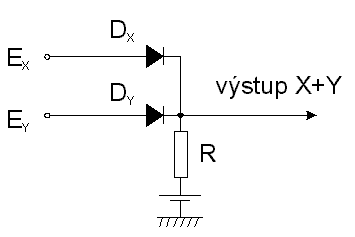
JestliĹže pĹedpoklĂĄdĂĄme ideĂĄlnĂ diody (tj. nekoneÄnĂ˝ odpor v zĂĄvÄrnĂŠm smÄru a nulovĂ˝ v propustnĂŠm smÄru), je funkce obvodu nĂĄsledujĂcĂ: Pro vstupnĂ napÄtĂ Ex > e nebo Ey > e je odpovĂdajĂcĂ dioda otevĹena a vĂ˝stupnĂ napÄtĂ kombinace je rovno Ex,y (pĹedpoklĂĄdĂĄme-li, Ĺže zdroje napÄtĂ Ex,y i  zdroj napÄtĂ e majĂ vnitĹnĂ odpor nulovĂ˝). Je-li napĹ. napÄtĂ Ex na vstupu X , pak dioda Dy je uzavĹenĂĄ, pokud napÄtĂ na vstupu Ey nenĂ vÄtĹĄĂ neĹž Ex. Pak se naopak zavĹe dioda Dx, vede Dy a vĂ˝stup kopĂruje napÄtĂ na vstupu Y.VĹĄimneme-li si vĂ˝stupnĂho odporu tohoto hradla vidĂme, Ĺže ve stavu logickĂŠ 0 je roven odporu R, ve stavu logickĂŠ 1 je nulovĂ˝. Pokud pouĹžĂvĂĄme reĂĄlnĂŠ diody a reĂĄlnĂŠ zdroje napÄtĂ logickĂ˝ch ĂşrovnĂ X a Y, musĂme poÄĂtat s jejich vnitĹnĂm odporem ri, odporem diod v propustnĂŠm smÄru a se zbytkovĂ˝m napÄtĂm na diodĂĄch UD (u germaniovĂ˝ch diod ~  0,2V, u kĹemĂkovĂ˝ch ~  0,7V). ZbytkovĂŠ napÄtĂ na diodĂĄch mĂĄ tu vĂ˝hodu, Ĺže nenĂ tĹeba pouĹžĂvat zdroj napÄtĂ, kterĂ˝ nĂĄm pĹedtĂm vytvĂĄĹel oblast napÄtĂ pro ĂşroveĹ logickĂŠ 0 (logickĂĄ 0 byla od 0V do e  V), neboĹĽ diody se neotevĹou, pokud vstupnĂ napÄtĂ nepĹekroÄĂ UD. Zahrneme-li odpor diod v propustnĂŠm smÄru do vnitĹnĂch odporĹŻ zdrojĹŻ logickĂ˝ch ĂşrovnĂ, bude pĹi aplikaci napÄtĂ Ex = E napÄtĂ na vĂ˝stupu rovno:
![]()
Jsou-li oba vstupy na Ăşrovni E , bude vĂ˝stupnĂ napÄtĂ
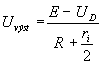
Výstupnà odpor hradla bude ve stavu logickÊ 1 roven
![]()
resp. ![]()
tedy pro
![]() je
je ![]() resp.
resp. ![]()
VidĂme, Ĺže i v takovĂŠmto
jednoduchĂŠm pĹĂpadÄ je nezbytnĂŠ, aby logickĂ˝ Älen
zpracovĂĄvajĂcĂ informaci z tohoto hradla byl necitlivĂ˝ na
zmÄnu ĂşrovnÄ logickĂŠ 1 v rozmezĂ ![]() a logickĂŠ 0 v rozmezĂ
a logickĂŠ 0 v rozmezĂ ![]()
ElektronickĂ˝ model logickĂŠho souÄinu funkce AND, je zobrazen na obr. 7.3 spolu s pravdivostnĂ tabulkou. Funkci hradla lze z obrĂĄzku snadno odvodit; pĹipomeĹme jen, Ĺže u tohoto hradla je vĂ˝stupnĂ odpor roven R pĹi Ăşrovni logickĂŠ jedniÄky (tedy naopak neĹž u diodovĂŠho hradla OR) a bude roven vnitĹnĂmu odporu diody (resp. jeho polovinÄ) ve stavu logickĂŠ 0. Je tedy vĂ˝stup hradla vysokoohmovĂ˝ ve stavu logickĂŠ 1 a nĂzkoohmovĂ˝ ve stavu logickĂŠ 0; naopak neĹž u diodovĂŠho hradla OR. PodobnÄ jako v pĹĂpadÄ hradla OR si ÄtenĂĄĹ mĹŻĹže ovÄĹit platnost zĂĄkonĹŻ agresivnosti a neutrĂĄlnosti.
Je nasnadÄ, Ĺže vzhledem k platnosti zĂĄkona asociativnĂho pro konjunkci i disjunkci lze vĂ˝razy
X = A1 A2 A3 A4 ..... An    a  Y = B1 + B2+ B3+ B4+ ..... + Bn Â
povaĹžovat za smysluplnĂŠ. V prvĂŠm pĹĂpadÄ bude X rovno 1 prĂĄvÄ kdyĹž vĹĄechny logickĂŠ promÄnnĂŠ Ai budou rovny 1 , ve druhĂŠm pĹĂpadÄ bude Y rovno 1 prĂĄvÄ kdyĹž alespoĹ jedna logickĂĄ promÄnnĂĄ Bi, bude rovna 1. Je rovnÄĹž zĹejmĂŠ, Ĺže u schĂŠmat uvedenĂ˝ch na obr. 7.2 a 7.3 lze zvÄtĹĄit poÄet vstupĹŻ hradel prostĂ˝m zvÄtĹĄenĂm poÄtu pĹĂsluĹĄnĂ˝ch vstupnĂch diod.
| X | Y | XY |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Funkci logickĂŠ inverze
âNOTâ je moĹžno vytvoĹit transistorovĂ˝m zesilovaÄem,
pracujĂcĂm ovĹĄem ne v lineĂĄrnĂm, ale ve spĂnacĂm reĹžimu.
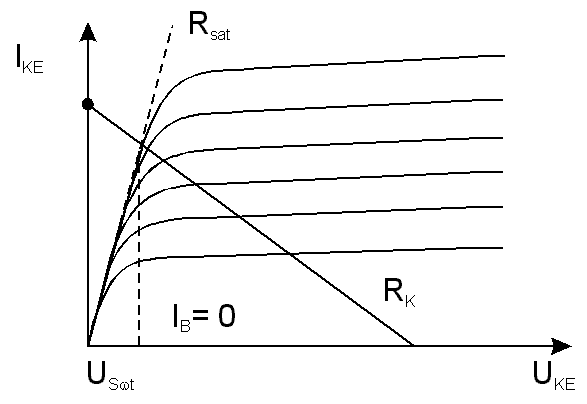
Je zĹejmĂŠ, Ĺže zapojĂme-li tranzistor do obvodu podle obr. 7.4
a budeme-li zvÄtĹĄovat proud do jeho bĂĄze, bude jeho
kolektorovĂŠ napÄtĂ klesat tak, jak to odpovĂdĂĄ jeho
vĂ˝stupnĂm charakteristikĂĄm a zatÄĹžovacĂ pĹĂmce. Od
urÄitĂŠho proudu bĂĄze vĹĄak zjistĂme, Ĺže napÄtĂ UKE
se prakticky nesniĹžuje -
transistor je ve stavu nasycenĂ. Je to stav, kdy jak emitorovĂ˝
pĹechod, tak kolektorovĂ˝ jsou pĂłlovĂĄny v propustnĂŠm smÄru,
a napÄtĂ mezi kolektorem s emitorem je v podstatÄ dĂĄno
rozdĂlem napÄtĂ na pĹechodu bĂĄze-emitor a na pĹechodu
bĂĄze - kolektor.
Prakticky u kĹemĂkovĂŠho tranzistoru je toto tzv. saturaÄnĂ
napÄtĂ Usat
ĹĂĄdu 0,2 V a u germaniovĂŠho tranzistoru ĹĂĄdu 0,1 V. BĂĄze
je pĹi tom nasycena minoritnĂmi nosiÄi nĂĄboje a veĹĄkerĂ˝
pĹĂrĹŻstek proudu bĂĄze jde na Ăşkor pĹĂrĹŻstku proudu
emitoru. PĹi zvyĹĄovĂĄnĂ kolektorovĂŠho proudu Usat roste; tuto zĂĄvislost lze aproximovat
pĹĂmkou a jejĂ smÄrnice se nazĂ˝vĂĄ saturaÄnĂ odpor Rsat. Tato pĹĂmka neprochĂĄzĂ
poÄĂĄtkem; jejĂ rovnice je ![]() , kde
, kde ![]() zĂĄvisĂ na
vlastnostech tranzistoru; je obvykle
zĂĄvisĂ na
vlastnostech tranzistoru; je obvykle ![]() . PĹestaneme-li dodĂĄvat proud do
bĂĄze tranzistoru, uzavĹou se obÄ diody (BE, BK) a pĹebytek
minoritnĂch nosiÄĹŻ v bĂĄzi je opÄt odsĂĄvĂĄn el. polem v
oblasti kolektorovĂŠho pĹechodu. Je zĹejmĂŠ, Ĺže ÄĂm vĂce
minoritnĂch nosiÄĹŻ bylo v bĂĄzi pĹed vypnutĂm, tĂm dĂŠle
bude trvat, neĹž kolektor odsaje vĹĄechny minoritnĂ nosiÄe v
båzi a kolektorový proud klesne na nulu. Proto je vhodnÊ
zabezpeÄit, aby tranzistor
. PĹestaneme-li dodĂĄvat proud do
bĂĄze tranzistoru, uzavĹou se obÄ diody (BE, BK) a pĹebytek
minoritnĂch nosiÄĹŻ v bĂĄzi je opÄt odsĂĄvĂĄn el. polem v
oblasti kolektorovĂŠho pĹechodu. Je zĹejmĂŠ, Ĺže ÄĂm vĂce
minoritnĂch nosiÄĹŻ bylo v bĂĄzi pĹed vypnutĂm, tĂm dĂŠle
bude trvat, neĹž kolektor odsaje vĹĄechny minoritnĂ nosiÄe v
båzi a kolektorový proud klesne na nulu. Proto je vhodnÊ
zabezpeÄit, aby tranzistor
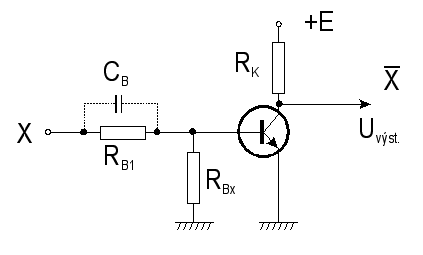
v sepnutÊm stavu pracoval na
okraji oblasti nasycenĂ: to lze dosĂĄhnout napĹ. pouĹžitĂm
tzv. desaturaÄnĂch diod (viz dalĹĄĂ odstavec), zapojenĂ˝ch
mezi båzi a kolektor. Kondenzåtor CB
napomĂĄhĂĄ urychlenĂ
pĹechodovĂŠho procesu odstranÄnĂ minoritnĂch nosiÄĹŻ
z bĂĄze, kdyĹž mÄnĂme napÄtĂ vstupu z 1 na 0. Funkce obvodu
na obr. 7.4 je tedy nĂĄsledujĂcĂ: pĹi aplikaci napÄtĂ
o logickĂŠ Ăşrovni 1 na vstup X invertoru zvÄtĹĄĂme proud
bĂĄze natolik, Ĺže tranzistor uvedeme do saturace. Na
vĂ˝stupu ![]() je tedy napÄtĂ Usat,
kterĂŠ je obvykle 1/4 aĹž 1/3 povolenĂŠho rozsahu napÄtĂ pro
logickou 0. PĹivedeme-li na vstup zaĹĂzenĂ napÄtĂ
o logickÊ úrovni 0, je tranzistor vypnut a na jeho kolektoru
(tedy na vĂ˝stupu invertoru) je plnĂŠ napĂĄjecĂ napÄtĂ volenĂŠ
tak, aby odpovĂdalo Ăşrovni logickĂŠ 1. Obvod tedy plnĂ
logickou funkci negace.
je tedy napÄtĂ Usat,
kterĂŠ je obvykle 1/4 aĹž 1/3 povolenĂŠho rozsahu napÄtĂ pro
logickou 0. PĹivedeme-li na vstup zaĹĂzenĂ napÄtĂ
o logickÊ úrovni 0, je tranzistor vypnut a na jeho kolektoru
(tedy na vĂ˝stupu invertoru) je plnĂŠ napĂĄjecĂ napÄtĂ volenĂŠ
tak, aby odpovĂdalo Ăşrovni logickĂŠ 1. Obvod tedy plnĂ
logickou funkci negace.
Rozvoj ÄĂslicovĂŠ mikroelektroniky si lze jen tÄĹžko pĹedstavit bez aplikace integrovanĂ˝ch obvodĹŻ. Jsou to obvody, kterĂŠ na destiÄce velikosti nÄkolika ÄtvereÄnĂch milimetrĹŻ soustĹeÄujĂ Ĺadu elektronickĂ˝ch prvkĹŻ, tj. tranzistorĹŻ, diod, odporĹŻ. Podle technologie vĂ˝roby rozliĹĄujeme integrovanĂŠ obvody na hybridnĂ a monolitickĂŠ.
HybridnĂ integrovanĂŠ obvody obsahujĂ pasivnĂ a aktivnĂ souÄĂĄstky, kterĂŠ se pĹipevnĂ na jednu nosnou destiÄku, vzĂĄjemnÄ propojĂ a zapouzdĹĂ. PĹitom aktivnĂmi souÄĂĄstkami nemusĂ bĂ˝t jednotlivĂŠ tranzistory, ale i monolitickĂŠ integrovanĂŠ obvody (tzv. Äipy). PĹĂkladem takovĂ˝ch obvodĹŻ mĹŻĹže bĂ˝t operaÄnĂ zesilovaÄ, obsahujĂcĂ kromÄ Äipu monolitickĂŠho operaÄnĂho zesilovaÄe, takĂŠ kompenzaÄnĂ kondenzĂĄtory a Ĺadu vstupnĂch a zpÄtnovazebnĂch odporĹŻ. ObecnÄ je moĹžno ĹĂci, Ĺže se touto technologiĂ vyrĂĄbÄjĂ obvody, kterĂŠ ke svĂŠ funkci potĹebujĂ stabilnĂ a pĹesnĂŠ odpory. TakovĂŠto odporovĂŠ sĂtÄ se monolitickou technologiĂ vyrĂĄbÄjĂ obtĂĹžnÄ a je proto lĂŠpe je vyrobit zvlĂĄĹĄĹĽ, napĹĂklad technologiĂ napaĹenĂ˝ch tenkĂ˝ch vrstev odporovĂŠho materiĂĄlu a nĂĄslednou laserovou kalibracĂ.
V monolitickĂ˝ch integrovanĂ˝ch obvodech jsou vĹĄechny potĹebnĂŠ prvky soustĹedÄny na jedinĂŠ destiÄce polovodiÄe, nejbÄĹžnÄji kĹemĂku. TechnologickĂ˝m postupem jsou na tĂŠto destiÄce vytvoĹeny jak aktivnĂ, tak pasivnĂ prvky i vzĂĄjemnĂŠ propoje souÄĂĄstek. PouzdĹenĂ takovĂŠho obvodu probĂhĂĄ tak, Ĺže se pouze propojĂ kontaktovacĂ ploĹĄky na destiÄce s vĂ˝vody pouzdra. O rĹŻznĂ˝ch technologiĂch vĂ˝roby integrovanĂ˝ch obvodĹŻ se mĹŻĹže ÄtenĂĄĹ doÄĂst v bÄĹžnÄ dostupnĂŠ literatuĹe.
NaprostĂĄ vÄtĹĄina elektronickĂ˝ch ÄĂslicovĂ˝ch systĂŠmĹŻ je vyrĂĄbÄna monolitickou technologiĂ. HybridnĂ obvody se pouĹžĂvajĂ vÄtĹĄinou jen u pĹevodnĂkĹŻ ÄĂslo-analog a analog-ÄĂslo. V tomto odstavci se soustĹedĂme na monolitickĂŠ integrovanĂŠ logickĂŠ systĂŠmy a popĂĹĄeme si jejich pĹednosti a nedostatky. Podle stupnÄ integrace rozliĹĄujeme malou integraci (SSI, small scale integration); sestĂĄvĂĄ se z mĂŠnÄ neĹž cca 15 logickĂ˝ch obvodĹŻ v jednom Äipu. JestliĹže je na jednom Äipu vĂce neĹž 15 a mĂŠnÄ neĹž 100 logickĂ˝ch obvodĹŻ, mluvĂme o obvodu se stĹednĂm stupnÄm integrace (MSI, medium scale integration). Obvody velkĂŠ integrace (LSI, large scale integration) majĂ v jednom Äipu logickĂ˝ch obvodĹŻ vĂce neĹž sto. SouÄasnĂŠ mikroprocesory a ÄipovĂŠ sady osobnĂch poÄĂtaÄĹŻ jsou obvody velmi velkĂŠho stupnÄ integrace (ELSI, extremely large scale of integration); u mikroprocesoru i486 se jednĂĄ o cca 1,2 milionu aktivnĂch polovodiÄovĂ˝ch prvkĹŻ na jednom Äipu, u Pentia je to cca 3x vĂce.
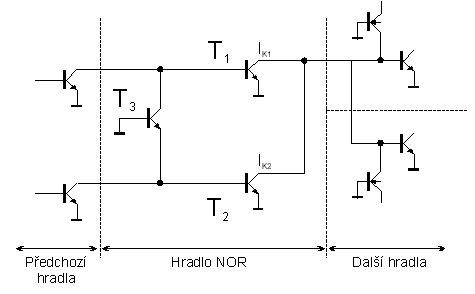
PĹĂmo vĂĄzanĂĄ tranzistorovĂĄ logika DCTL (Direct-Coupled-Transistor-Logic) je nejjednoduĹĄĹĄĂm typem logiky, kterĂ˝ ve svĂŠ skladbÄ pouĹžĂvĂĄ tranzistorĹŻ. ZĂĄkladnĂm hradlem tÄchto obvodĹŻ je hradlo NOR, kterĂŠ je znĂĄzornÄno na obr. 7.5.
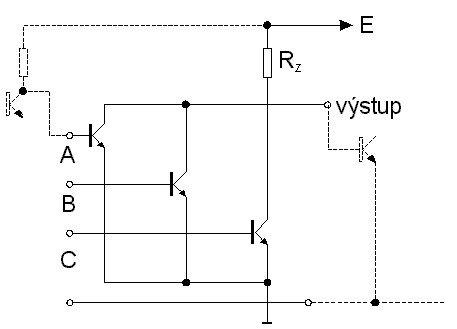
Obvod je tvoĹen nÄkolika tranzistory s propojenĂ˝mi a uzemnÄnĂ˝mi emitory a spoleÄnĂ˝m kolektorovĂ˝m odporem. Je zĹejmĂŠ, Ĺže staÄĂ, aby jeden z tranzistorĹŻ byl vybuzen do saturace a jiĹž napÄtĂ na vĂ˝stupu klesne na jeho saturaÄnĂ napÄtĂ, tj. na napÄtĂ ĹĂĄdu 0,1 V. OtevĹenĂ eventuĂĄlnĂch dalĹĄĂch tranzistorĹŻ nezpĹŻsobĂ jiĹž podstatnou zmÄnu vĂ˝stupnĂho napÄtĂ. Hradla jsou v tomto systĂŠmu propojena pĹĂmo jak je takĂŠ ukĂĄzĂĄno na obr. 7.5. Proto napÄtĂ na vĂ˝stupu tohoto hradla v nevybuzenĂŠm stavu zpravidla nepĹekroÄĂ ĂşroveĹ 1 V (je omezeno napÄtĂm na diodÄ bĂĄze-emitor nĂĄsledujĂcĂho hradla). PĹedpokladem pro sprĂĄvnou funkci systĂŠmu tÄchto hradel je naprostĂĄ shoda charakteristik jednotlivĂ˝ch tranzistorĹŻ, jinak tranzistor s niŞťĂm napÄtĂm bĂĄze-emitor spotĹebuje vÄtĹĄinu proudu plynoucĂho z kolektorovĂŠho odporu pĹedchĂĄzejĂcĂho hradla a tranzistory s vyĹĄĹĄĂm napÄtĂm bĂĄze-emitor zĹŻstanou nevybuzeny. TĂm vznikajĂ potĂĹže propojovĂĄnĂ jednotlivĂ˝ch hradel mezi sebou, pokud nenĂ systĂŠm umĂstÄn na jedinĂŠm Äipu. Tento systĂŠm proto nedosĂĄhl ĹĄirĹĄĂho uplatnÄnĂ v praxi; myĹĄlenka se vĹĄak uplatnila u systĂŠmu I2L..
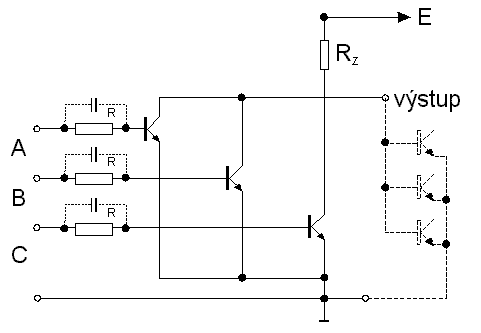
Aby se redukoval efekt nestejných charakteristik tranzistorů,
byly vloĹženy odpory do bĂĄzovĂ˝ch pĹĂvodĹŻ kaĹždĂŠho
tranzistoru. TĂm vznikla tzv. odporovÄ-tranzistorovĂĄ logika
RTL (Resistor-Transistor-Logic). Obvody tĂŠto logiky se jiĹž po
urÄitou dobu vyrĂĄbÄly v integrovanĂŠ formÄ, postupnÄ vĹĄak
byly vytlaÄeny jinĂ˝mi systĂŠmy s lepĹĄĂmi parametry. ZĂĄkladnĂm hradlem je
zde opÄt NOR, jehoĹž schĂŠma je na obr. 7.6. ZaĹazenĂm odporĹŻ
do bĂĄzĂ tranzistorĹŻ se rovnÄĹž zvýťila schopnost hradla
budit vĂce nĂĄsledujĂcĂch logickĂ˝ch obvodĹŻ. Proti pĹĂmo
vĂĄzanĂŠ logice se vĹĄak snĂĹžila spĂnacĂ rychlost obvodu, neboĹĽ parazitnĂ kapacity se
nynĂ musely nabĂjet pĹes vÄtĹĄĂ odpor. Proto se nÄkdy
pĹidĂĄvaly paralelnÄ ke vstupnĂm odporĹŻm tzv. urychlovacĂ
kondenzĂĄtory (na obr. 7.6 ÄĂĄrkovanÄ), kterĂŠ tvoĹily s
parazitnĂ vstupnĂ kapacitou kapacitnĂ dÄliÄ napÄtĂ.
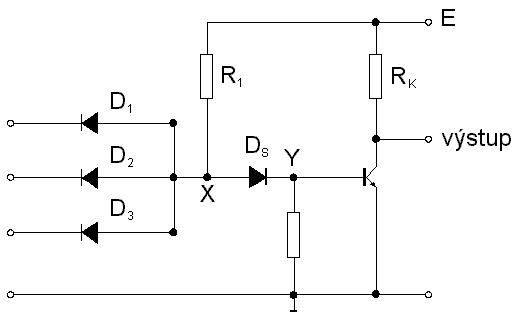
SystĂŠm diodovĂŠ tranzistorovĂŠ logiky DTL (Diode-Transistor-Logic) je jednĂm z obvodĹŻ, kterĂŠ se pro speciĂĄlnĂ ĂşÄely jeĹĄtÄ vyrĂĄbÄjĂ. ZĂĄkladnĂm hradlem tohoto systĂŠmu je NAND a vzniklo v podstatÄ kombinacĂ diodovĂŠho obvodu AND s invertorem - obr. 7.7. Dioda DS zajiĹĄĹĽuje, Ĺže tranzistor zĹŻstane uzavĹen, pakliĹže alespoĹ jeden ze vstupĹŻ je uzemnÄn, tj. v bodÄ X je napÄtĂ rovnĂŠ spĂĄdu na pĹĂsluĹĄnĂŠ diodÄ a v bodÄ Y je napÄtĂ nulovĂŠ. Jako DS se obvykle uĹžĂvajĂ dvÄ diody v sĂŠrii, ÄĂmĹž se zvÄtĹĄĂ ĹĄumovĂĄ imunita hradla. OdporovĂ˝ dÄliÄ v bĂĄzi invertoru je volen tak, aby v pĹĂpadÄ logickĂ˝ch jedniÄek na vstupech byl tranzistor saturovĂĄn. VstupnĂ odpor hradla je velkĂ˝, je-li vstup na Ăşrovni logickĂŠ 1 a rovnĂĄ se prakticky R1, je-li vstup na Ăşrovni logickĂŠ 0. VĂ˝stupnĂ odpor ve stavu logickĂŠ 1 je roven kolektorovĂŠmu odporu a ve stavu logickĂŠ nuly je velmi malĂ˝. Hradla se tedy dajĂ snadno Ĺadit za sebe, typickĂŠ zpoĹždÄnĂ signĂĄlu na jedno hradlo je 25 ns. VĂ˝roba v monolitickĂŠ formÄ nenĂ obtĂĹžnĂĄ. Koncepce systĂŠmu skĂ˝tĂĄ moĹžnost zaĹadit mĂsto diody DS Zenerovu diodu a tĂm zĂskat systĂŠm s extrĂŠmnÄ vysokou ĹĄumovou imunitou.
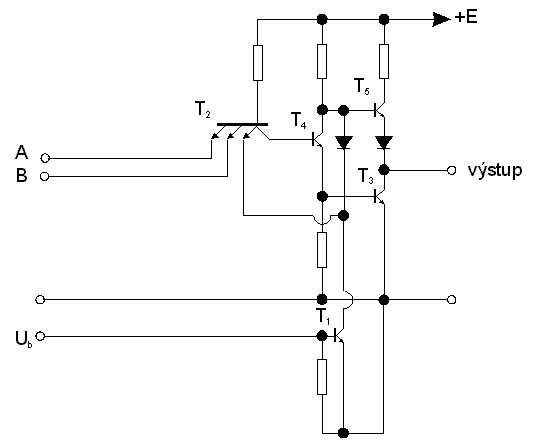
NejvÄtĹĄĂho rozĹĄĂĹenĂ dosĂĄhly ve svĂŠ dobÄ integrovanĂŠ logickĂŠ systĂŠmy TTL (Transistor-Transistor-Logic). V dneĹĄnĂ dobÄ jsou vĹĄak nahrazovĂĄny systĂŠmy STTL, MOS a CMOS, kterĂŠ majĂ niŞťà spotĹebu a srovnatelnou rychlost. Zachovala se vĹĄak definice logickĂ˝ch ĂşrovnĂ; pokud mĂĄ modernĂ logickĂ˝ systĂŠm stejnÄ definovanĂŠ napÄĹĽovĂŠ ĂşrovnÄ logickĂŠ nuly a jedniÄky, nazĂ˝vĂĄ se kompatibilnĂ s TTL na logickĂ˝ch ĂşrovnĂch (logic level TTL compatible). V tÄchto obvodech jsou vstupnĂ diody nahrazeny vĂceemitorovĂ˝m tranzistorem. VĂceemitorovĂ˝ tranzistor se totiĹž relativnÄ snadno vyrĂĄbĂ standardnĂ planĂĄrnĂ technologiĂ a jeho vĂ˝roba je ekonomiÄtÄjĹĄĂ neĹž vĂ˝roba nÄkolika izolovanĂ˝ch diod. NavĂc pĹi bÄĹžnĂŠm provozu jsou hradla TTL rychlejĹĄĂ neĹž DTL zhruba 2x; typickĂĄ hodnota zpoĹždÄnĂ se pohybuje okolo 12 ns. ZĂĄkladnĂm hradlem je opÄt NAND, kterĂŠ je nakresleno na obr. 7.8.
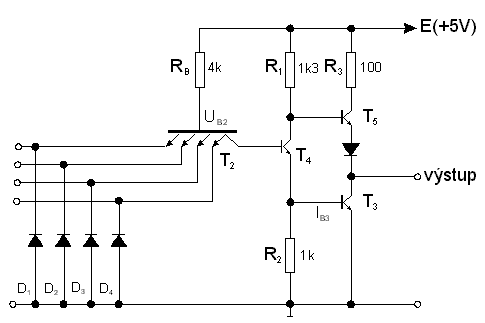
Aby byla umoĹžnÄna vyĹĄĹĄĂ zatĂĹžitelnost hradla, je na konci hradla zabudovĂĄn koncovĂ˝ stupeĹ. Z dĹŻvodĹŻ omezenĂ zĂĄpornĂ˝ch napÄĹĽovĂ˝ch ĹĄpiÄek na vstupech hradla byly vstupy opatĹeny ochrannĂ˝mi diodami, kterĂŠ nedovolĂ vyĹĄĹĄĂ zĂĄpornĂŠ napÄtĂ na vstupech neĹž cca -0,6V. Funkce obvodu je nĂĄsledujĂcĂ:
a. VĹĄechny vstupy jsou ve stavu logickĂŠ jedniÄky.
V tomto pĹĂpadÄ tranzistor T2 pracuje v inverznĂm reĹžimu. Tranzistor T4 je saturovĂĄn a tranzistor T3 je vybuzen. NapÄtĂ na kolektoru tranzistoru T4 je pĹibliĹžnÄ UD + Ukesat. Aby byl tranzistor T5 uzavĹen (mĂĄ na bĂĄzi napÄtĂ Uk4) je do obvodu vloĹžena dioda D, kterĂĄ posunuje napÄtĂ emitoru T5 na napÄtĂ Ukesat+UD. Tranzistor T3 je tedy otevĹen a T5 uzavĹen. Na vĂ˝stupu je napÄtĂ Ukesat, coĹž je napÄtĂ logickĂŠ 0.
b. Jeden nebo vĂce vstupĹŻ jsou ve stavu logickĂŠ nuly.
Pak je tranzistor T4Â a
rovnÄĹž T3
uzavĹen a odpor R1 zaruÄuje nasycenĂ tranzistoru T5.
Ten slouŞà nynĂ jako emitorovĂ˝ sledovaÄ pro vĂ˝stupnĂ
napÄtĂ, takĹže mĹŻĹže do zĂĄtÄĹže dodat podstatnÄ vÄtĹĄĂ
proud neĹž tomu bylo u pĹedchozĂho zapojenĂ. NapÄtĂ na
vĂ˝stupu je menĹĄĂ neĹž E o spĂĄd na diodÄ bĂĄze-emitor
tranzistoru T5 a
na diodÄ D, je tedy U1 Âť
E - 2 UD. Je
uĹžiteÄnĂŠ si vĹĄimnout, Ĺže napĂĄjecĂ napÄtĂ E nemĹŻĹžeme
libovolnÄ zmenĹĄovat. Je-li totiĹž T3 otevĹen, je napÄtĂ na bĂĄzi T2
napÄtĂ UB2  3UD. Aby T2 pracoval v inverznĂm reĹžimu, je
tĹeba, aby napÄtĂ na emitoru T2 bylo vÄtĹĄĂ neĹž toto napÄtĂ.
Vzhledem k tomu, Ĺže emitorovĂŠ napÄtĂ T2 je vlastnÄ vĂ˝stupnĂ napÄtĂ
pĹedchĂĄzejĂcĂho hradla stejnĂŠho typu (ve stavu logickĂŠ
jedniÄky), musĂ bĂ˝t U1> UB2
neboli EÂ >Â 5UD.
MinimĂĄlnĂ napÄtĂ logickĂŠ jedniÄky musĂ tedy bĂ˝t U1 > 3UD.
Na TTL hradlo v uvedenĂŠm
zapojenĂ mĹŻĹže bĂ˝t zapojeno aĹž 15 dalĹĄĂch hradel stejnĂŠho
typu. TypickĂŠ zpoĹždÄnĂ pĹi prĹŻchodu hradla je  Ĺ 10 ns a vĂ˝konovĂĄ ztrĂĄta Ĺ 15 mW.
DvojÄinnĂ˝ stupeĹ neumoĹžĹuje propojenĂ nÄkolika vĂ˝stupĹŻ popsanĂ˝ch hradel NAND paralelnÄ. K tomu je zapotĹebĂ dalĹĄĂho hradla typu OR. Toto hradlo vĹĄak mĹŻĹžeme vypustit, jestliĹže pouĹžijeme hradel s tzv. otevĹenĂ˝m kolektorem. PrincipiĂĄlnĂ zapojenĂ hradla NAND s otevĹenĂ˝m kolektorem je na obr. 7.9.
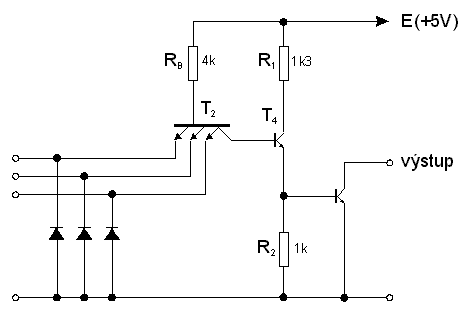
Do vĂ˝stupnĂho obvodu je nutnĂŠ zapojit vnÄjĹĄĂ odpor, na kterĂ˝ vĹĄak mĹŻĹžeme pĹipojit dalĹĄĂ hradlo s otevĹenĂ˝m kolektorem.
SpojenĂm nÄkolika vĂ˝stupĹŻ s otevĹenĂ˝m kolektorem pĹes vnÄjĹĄĂ odpor vznikne funkce âmontĂĄĹžnĂho ANDâ. ProtoĹže vĹĄak vÄtĹĄinou spojujeme negovanĂŠ vĂ˝stupy hradel (funkce NAND) vytvoĹĂ se (pouĹžitĂm transformace pomocĂ de Morganova teorĂŠmu) funkce âmontĂĄĹžnĂho ORâ (wired OR). PĹĂklad paralelnĂho zapojenĂ dvou hradel je na obr 7.10. EkvivalentnĂ schema zapojenĂ je na obr. 7.11. a logickĂĄ funkce je dĂĄna nĂĄsledujĂcĂm BooleovskĂ˝m vĂ˝razem:
![]() .
.

LogickĂŠ systĂŠmy, kterĂŠ byly dosud popsĂĄny, jsou vyrĂĄbÄny s rĹŻznĂ˝m poÄtem vstupĹŻ a na jednom Äipu bĂ˝vĂĄ umĂstÄno vĂce hradel. Tak napĹĂklad obvod 7400 je ÄtveĹice dvojvstupovĂ˝ch hradel NAND systĂŠmu TTL. Abychom z takovĂ˝chto logickĂ˝ch ÄlenĹŻ vytvoĹili poĹžadovanou logickou funkci, je tĹeba vybrat z vyrĂĄbÄnĂ˝ch typĹŻ a propojit na destiÄce s tiĹĄtÄnĂ˝mi spoji. Je-li logickĂĄ funkce sloĹžitĂĄ, bude tĹeba Ĺady logickĂ˝ch ÄlenĹŻ a celĂ˝ systĂŠm bude mĂt nĂĄsledujĂcĂ zjevnĂŠ nevĂ˝hody:
1. RelativnÄ vysokĂĄ cena potĹebnĂ˝ch logickĂ˝ch ÄlenĹŻ,
2. relativnÄ vysokĂĄ cena nĂĄvrhu, provedenĂ, osazenĂ a oĹživenĂ ploĹĄnĂŠho spoje,
3. parazitnĂ kapacity a indukÄnosti spojĹŻ mohou pĹŻsobit problĂŠmy pĹi zvyĹĄovĂĄnĂ rychlosti systĂŠmu,
4. je-li systĂŠm sloĹžitĂ˝, vÄtĹĄinou nenĂ moĹžnĂŠ vyuĹžĂt vĹĄechny vstupy pouzder, aniĹž bychom neĂşmÄrnÄ zkomplikovali propojenĂ pouzder.
To znamenĂĄ, Ĺže Ĺada funkcĂ zĹŻstane nevyuĹžita.
Abychom tyto nevĂ˝hody obeĹĄli, musĂme pĹejĂt k vysokĂŠmu stupni integrace logickĂ˝ch ÄlenĹŻ na jedinĂŠm Äipu a pokud moĹžno zjednoduĹĄit obvody jedinĂŠho hradla. To vĹĄe ovĹĄem pĹi zachovĂĄnĂ vysokĂŠ rychlosti hradla a pokud moĹžno minimĂĄlnĂho pĹĂkonu. Velice slibnĂ˝m systĂŠmem je tzv. integrovanĂĄ injekÄnĂ logika (I2L) zvanĂĄ tĂŠĹž logika se sdruĹženĂ˝m tranzistorem MTL (Merged-Transistor-Logic); tento systĂŠm, jehoĹž zĂĄkladnĂ dvojvstupovĂŠ hradlo je na obr. 7.12 spolu s napĂĄjecĂmi a zatÄĹžovacĂmi obvody, nepouĹžĂvĂĄ v podstatÄ pasivnĂ prvky - odpory. VhodnĂ˝m nĂĄvrhem se navĂc dosĂĄhlo toho, Ĺže ani mezi jednotlivĂ˝mi tranzistory ani mezi hradly nenĂ tĹeba pĹi vĂ˝robÄ difundovat izolaÄnĂ pĹĂkopy, coĹž podstatnÄ zjednoduĹĄilo technologii vĂ˝roby. SouÄin pĹĂkon x zpoĹždÄnĂ dosĂĄhl ĹĂĄdovÄ desetin pJ (10-12 J), coĹž je zhruba o 2 - 3 ĹĂĄdy mĂŠnÄ neĹž obvody TTL. ZĂĄkladnĂm hradlem tohoto systĂŠmu je NOR a lze rovnÄĹž snadno realizovat inverzi, tj. operaci NOT. DvojvstupovĂŠ hradlo se sklĂĄdĂĄ v podstatÄ ze tĹĂ tranzistorĹŻ, dvou struktury NPN (T1 a T2 na obr. 7.17) a jednoho PNP se dvÄma kolektory (T3 na obr. 7.12). BĂĄze T3 a emitory T1 a T2 tvoĹĂ spoleÄnĂĄ zĂĄkladnĂ destiÄka z polovodiÄe typu N.
KolektorovĂŠ oblasti T3 jsou sdruĹženy s bĂĄzovĂ˝mi oblastmi T1 a T2 tak, Ĺže napĹ. hornĂ kolektor T3 a bĂĄze T1 tvoĹĂ jednu difundovanou oblast P v zĂĄkladnĂ destiÄce polovodiÄe typu N. Emitor T3 tvoĹĂ dalĹĄĂ difundovanou oblast P, geometricky uspoĹĂĄdanou tak, aby proud zavĂĄdÄnĂ˝ do emitoru T3 se dÄlil rovnomÄrnÄ do bĂĄzĂ T1 a T2. Tranzistor T3 tak tvoĹĂ injektor, kterĂ˝ postaÄĂ zĂĄsobovat bĂĄze T1 a T2 minoritnĂmi nosiÄi nĂĄboje v takovĂŠ mĂĹe, Ĺže oba tranzistory jsou v saturaci. Proud do emitoru T3 se zĂskĂĄ jednoduĹĄe tak, Ĺže se vĹĄechny emitory na spoleÄnĂŠm Äipu propojĂ a pĹipojĂ se pĹes jedinĂ˝ odpor ke zdroji kladnĂŠho napĂĄjecĂho napÄtĂ obvodu (tento odpor mĹŻĹže bĂ˝t realizovĂĄn rovnÄĹž na tĂŠmĹže Äipu). Funkce obvodu je nĂĄsledujĂcĂ: Jsou-li oba budicĂ tranzistory pĹedchozĂch hradel uzavĹeny, injektor T3 saturuje oba tranzistory T1 a T2 a na jejich kolektorech bude saturaÄnĂ napÄtĂ Usat. Je-li jeden z budicĂch tranzistorĹŻ (napĹ. hornĂ) otevĹen, protĂŠkĂĄ jĂm proud injektoru a pĹĂsluĹĄnĂ˝ transistor (T1) zĹŻstane uzavĹen. NapÄtĂ na jeho kolektoru vĹĄak zĹŻstane rovnĂŠ Usat, neboĹĽ T2 je jeĹĄtÄ otevĹen. Jsou-li pak oba budĂcĂ tranzistory otevĹeny, tekou jimi proudy injektoru a oba T1 i T2 se uzavĹou. Na jejich kolektorech vystoupĂ napÄtĂ na hodnotu odpovĂdajĂcĂ spĂĄdu napÄtĂ na diodĂĄch BE NPN tranzistorĹŻ nĂĄsledujĂcĂho hradla. Obvod tedy plnĂ logickou funkci NOR , pĹiÄemĹž rozdĂl mezi logickou jedniÄkou a nulou je ĹĂĄdovÄ 0.5 - 0.6 V, tj. UD - Usat. Vzhledem k tĂŠto nĂzkĂŠ hodnotÄ se logickĂŠ ĂşrovnÄ pĹed vĂ˝stupem z Äipu transformujĂ na ĂşrovnÄ TTL, aby byla zvýťena odolnost proti ruĹĄenĂ. UvnitĹ Äipu je ĹĄumovĂĄ imunita velmi dobrĂĄ. Jednoduchost systĂŠmĹŻ MTL-I2L umoĹžĹuje hustotu aĹž 400 hradel/mm2, coĹž odpovĂdĂĄ cca 1000-3000 hradel na jednom Äipu.
AĹž dosud vybĂranĂŠ systĂŠmy obsahovaly tranzistor nebo tranzistory, kterĂŠ se dostateÄnĂ˝m bĂĄzovĂ˝m proudem uvĂĄdÄly do saturace a dosĂĄhlo se malĂŠho napÄtĂ mezi kolektorem a emitorem. Tento zpĹŻsob vĹĄak nenĂ vhodnĂ˝ chceme-li dĂĄle zvyĹĄovat rychlost hradel. U nasycenĂŠho tranzistoru vĹždy bude trvat urÄitou dobu, abychom odstranili pĹebyteÄnĂŠ minoritnĂ nosiÄe z bĂĄze a uvedli tranzistor do normĂĄlnĂho reĹžimu. Pro dalĹĄĂ snĂĹženĂ zpoĹždÄnĂ v hradlech je tĹeba buÄ (1) zabezpeÄit, aby tranzistory pracovaly v prĂĄvÄ saturovanĂŠm reĹžimu, kdy je nahromadÄnĂ˝ nĂĄboj minoritnĂch nosiÄĹŻ v bĂĄzi minimĂĄlnĂ, nebo (2) zabezpeÄit, aby tranzistory vĹŻbec v saturaci nepracovaly.
VĹĄimnÄme si nejprve prvnĂ moĹžnosti. Aby tranzistor nebyl uveden do hlubokĂŠ saturace, je tĹeba zabezpeÄit, aby napÄtĂ bĂĄze-kolektor UBC Ĺ 0 (u tranzistoru NPN). Je-li UBC @ 0, je tranzistor prĂĄvÄ saturovĂĄn. TĂŠto podmĂnky je moĹžnĂŠ dosĂĄhnout pomocĂ tzv. Schottkyho diod. Schottkyho diody jsou tvoĹeny pĹechodem typu kov-polovodiÄ, a majĂ voltampĂŠrovou charakteristiku velice podobnou diodÄ s pĹechodem P-N. (TĂm se liĹĄĂ od tzv. ohmickĂ˝ch kontaktĹŻ kov-polovodiÄ, jejichĹž vodivost nezĂĄleŞà na polaritÄ).

ZĂĄkladnĂ rozdĂl proti P-N diodÄ je vĹĄak ten, Ĺže proud Schottkyho diodou je tvoĹen pĹevĂĄĹžnÄ majoritnĂmi nosiÄi nĂĄboje, tedy elektrony, zatĂmco u P-N diody jsou rozhodujĂcĂ minoritnĂ nosiÄe. Proto Schottkyho dioda mĂĄ velmi malou dobu zotavenĂ. DalĹĄĂ vĂ˝hoda Schottkyho diod tkvĂ v tom,Ĺže napÄtĂ na nich v propustnĂŠm smÄru je zhruba 0,3 V, coĹž je cca polovina neĹž u kĹemĂkovĂŠ P-N diody. PĹi pouĹžitĂ Schottkyho diod jako desaturaÄnĂch diod invertoru zĂskĂĄme strukturu na obr. 7.13.a. PĹechod bĂĄze-kolektor tranzistoru je sice moĹžnĂŠ ÄĂĄsteÄnÄ pĂłlovat v propustnĂŠm smÄru, avĹĄak tato skuteÄnost nemĂĄ podstatnĂ˝ vliv na dobu zotavenĂ tranzistoru ve srovnĂĄnĂ s prĂĄvÄ saturovanĂ˝m stavem. SlabÄ kladnÄ pĂłlovanĂ˝ pĹechod bĂĄze-kolektor zpĹŻsobĂ vĹĄak pokles napÄtĂ UCEsat , kterĂŠ je podstatnÄ niŞťà neĹž UD. ZĂĄvislost doby zpoĹždÄnĂ invertoru na vstupnĂm proudu pro obvod bez saturace a s desaturaÄnĂ diodou je na obr. 7.13.b. Poznamenejme jeĹĄtÄ, Ĺže existujĂ rovnÄĹž zapojenĂ umoĹžĹujĂcĂ provĂŠst desaturaci invertoru s pouĹžitĂm normĂĄlnĂho tranzistoru. Tyto systĂŠmy jsou vĂ˝hodnĂŠ tam, kde nenĂ moĹžnĂŠ nebo ekonomickĂŠ zavĂĄdÄt do technologie vĂ˝roby dalĹĄĂ operaci (kterĂĄ je naopak nutnĂĄ pro vytvoĹenĂ Schottkyho diod).
PopsanĂŠ systĂŠmy, zejmĂŠna TTL a STTL jsou vhodnĂŠ a pouĹžĂvanĂŠ pro Ĺadu ÄĂslicovĂ˝ch zaĹĂzenĂ; jejich cena je relativnÄ nĂzkĂĄ a propojovĂĄnĂ na desce je prakticky bez problĂŠmĹŻ. NicmĂŠnÄ existujĂ aplikace, kde zĂĄkladnĂm poĹžadavkem je rychlost obvodu bez ohledu na spotĹebu, cenu a rozmÄry obvodu. Jako pĹĂklad je moĹžno uvĂŠst centrĂĄlnĂ procesory velkĂ˝ch poÄĂtaÄĹŻ, kde na rychlosti zĂĄvisĂ moĹžnosti nĂĄkladnĂ˝ch periferiĂ. PoÄĂtaÄ sĂĄm o sobÄ je znaÄnĂĄ investice, takĹže ponÄkud vyĹĄĹĄĂ cena, spotĹeba, event. rozmÄry obvodĹŻ v procesoru nehrajĂ takovou Ăşlohu, jako jeho rychlost. Proto byly vyvinuty logickĂŠ obvody, kde prakticky vĹŻbec nedochĂĄzĂ k saturaci tranzistorĹŻ, ÄĂmĹž se zhruba o ĹĂĄd snĂĹžila doba prĹŻchodu hradlem (vzhledem k logice TTL). DalĹĄĂho snĂĹženĂ doby prĹŻchodu se dosĂĄhlo snĂĹženĂm rozkmitu napÄtĂ mezi logickou nulou a jedniÄkou na ĹĂĄdovÄ 0,8 V.
ZĂĄkladnĂm hradlem tohoto systĂŠmu je hradlo OR/NOR, kterĂŠ sestĂĄvĂĄ prakticky z diferenciĂĄlnĂho zesilovaÄe, jehoĹž vĂ˝stupy jsou oddÄleny emitorovĂ˝mi sledovaÄi. Na jeden ze vstupĹŻ diferenciĂĄlnĂho zesilovaÄe je pĹevedeno referenÄnĂ napÄtĂ -UB , druhĂĄ vÄtev je znĂĄsobena na poÄet odpovĂdajĂcĂ poÄtu vstupĹŻ hradla. Princip funkce vysvÄtlĂme na obr.7.14. V emitorech tranzistorĹŻ diferenciĂĄlnĂho zesilovaÄe je na obr.7.14 znĂĄzornÄn zdroj proudu, coĹž vÄtĹĄinou bĂ˝vĂĄ prostĂ˝ odpor velikosti ĹĂĄdovÄ 1 kW  . NapÄĹĽovĂŠ ĂşrovnÄ jsou znĂĄzornÄny na obr. 7.15,
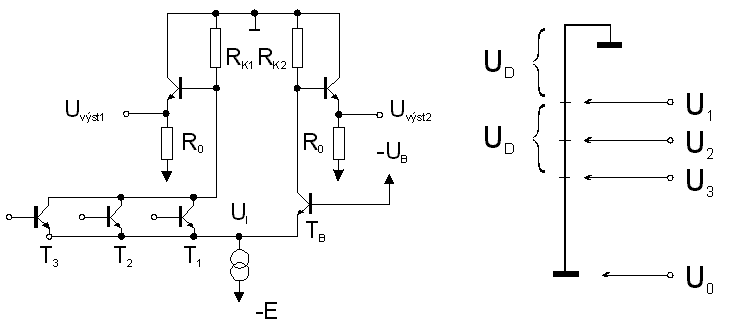
kde UD znaÄĂ opÄt napÄtĂ na otevĹenĂŠm pĹechodu bĂĄze-emitor pouĹžitĂ˝ch tranzistorĹŻ. NechĹĽ na vĹĄech vstupech hradla (tj. na bĂĄzĂch T1,T2 ,T3 )je napÄtĂ Uo. ProtoĹže Uo < UB, jsou tranzistory T1, T2, T3 zavĹeny a na vĂ˝stupu NOR je napÄtĂ -UD. To je tedy napÄtĂ logickĂŠ jedniÄky U1 = -UD. PĹiveÄme nynĂ alespoĹ na jeden vstup napÄtĂ U1 (napĹ. na bĂĄzi T1). Tranzistor T1 je blĂzek saturace, proto mĹŻĹžeme psĂĄt, Ĺže UK1  U1 a tedy UvĂ˝st  U1 - UD. To je tedy napÄtĂ logickĂŠ nuly
Uo  U1 - UD = - 2 UD.
VidĂme, Ĺže oba emitorovĂŠ sledovaÄe nejen Ĺže oddÄlujĂ vĂ˝stupy hradla, ale rovnÄĹž stejnosmÄrnÄ posouvajĂ vĂ˝stupnĂ logickĂŠ ĂşrovnÄ tak, aby byly kompatibilnĂ se vstupnĂmi. RozdĂl mezi logickou nulou a jedniÄkou se tedy rovnĂĄ UD. Tento systĂŠm logickĂ˝ch obvodĹŻ je rovnÄĹž pĹĂkladem na pozitivnĂ logiku, kdy obÄ logickĂŠ ĂşrovnÄ jsou zĂĄpornĂŠ.
Obvody ECL vznikly v roce 1962 a jiĹž v dobÄ svĂŠho vzniku mÄly nominĂĄlnĂ dobu prĹŻchodu hradlem 8 ns. SouÄasnĂŠ obvody majĂ tento parametr okolo 1 ns a je nutnĂŠ jiĹž peÄlivÄ volit propojenĂ jednotlivĂ˝ch obvodĹŻ, aby nedochĂĄzelo ke zbyteÄnĂ˝m zpoĹždÄnĂm signĂĄlu pĹi prĹŻchodu spoji. NavĂc zde pĹistupuje problĂŠm pĹizpĹŻsobenĂ vĂ˝stupnĂho a vstupnĂho odporu hradel charakteristickĂŠ impedanci spojĹŻ, jinak odrazy na koncĂch vedenĂ mohou zcela znehodnotit pĹenĂĄĹĄenou informaci. Proto se propojenĂ jednotlivĂ˝ch pouzder pro extrĂŠmnÄ rychlĂŠ systĂŠmy navrhuje vÄtĹĄinou na poÄĂtaÄĂch a realizuje se pomocĂ vĂcevrstvovĂ˝ch (6 - 14 vrstev spojĹŻ) ploĹĄnĂ˝ch spojĹŻ. Aby zpoĹždÄnĂ mezi obvody bylo co nejmenĹĄĂ, volĂ se velkĂĄ hustota souÄĂĄstek, coĹž vede ke znaÄnÄ tenkĂ˝m spojĹŻm (ĹĄĂĹka propojovacĂch Äar okolo 0,l5 mm).
NejvÄtĹĄĂ zisk z rychlosti obvodĹŻ ECL dostaneme vÄtĹĄĂ integracĂ tÄchto obvodĹŻ na jedinĂŠm Äipu, kde dĂŠlka propojenĂ jednotlivĂ˝ch hradel je v ĹĂĄdu setin mm. NapĹ. 256 bitovĂĄ ECL pamÄĹĽ mĂĄ maximĂĄlnĂ dobu vybavenĂ pouze 25 ns a pouĹžĂvĂĄ se jako tzv. zĂĄpisnĂkovĂĄ pamÄĹĽ aritmeticko-logickĂŠ jednotky velkĂ˝ch poÄĂtaÄĹŻ. Je moĹžno ĹĂci, Ĺže obvody ECL jsou zatĂm nejrychlejĹĄĂ ze vĹĄech logickĂ˝ch systĂŠmĹŻ, avĹĄak jejich spotĹeba i cena je relativnÄ vysokĂĄ.
Jednou z podmĂnek k opravdu masovĂŠmu rozĹĄĂĹenĂ mikroelektroniky je malĂĄ spotĹeba zaĹĂzenĂ, kterĂĄ umoĹžĹuje napĂĄjet pĹĂstroj z bateriĂ. MoĹžnost malĂŠ spotĹeby otevĹely logickĂŠ systĂŠmy s tranzistory ĹĂzenĂ˝mi polem MOSFET a zejmĂŠna systĂŠmy CMOS.
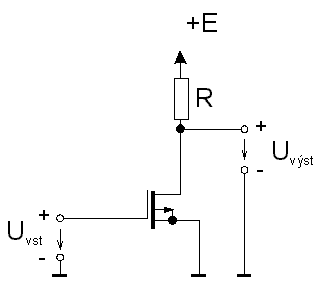
ZĂĄkladem systĂŠmĹŻ MOS je opÄt invertor, ovĹĄem s tranzistorem ĹĂzenĂ˝m elektrickĂ˝m polem. PouĹžĂvajĂ se tranzistory s indukovanĂ˝m kanĂĄlem, kterĂŠ majĂ vhodnou polaritu tzv. prahovĂŠho napÄtĂ. PrahovĂŠ napÄtĂ Up je napÄtĂ na ĹĂdicĂ elektrodÄ G (hradlu) tranzistoru, pĹi kterĂŠm protĂŠkĂĄ transistorem urÄitĂ˝ malĂ˝ definovanĂ˝ proud (napĹ. 10 nA); tranzistor je pĹi tom napĂĄjen definovanĂ˝m napÄtĂm, napĹ. 10 V. Je zĹejmĂŠ, Ĺže v zĂĄjmu zjednoduĹĄenĂ napĂĄjenĂ zaĹĂzenĂ je tĹeba, abychom tranzistor âzavĹeliâ napÄtĂm stejnĂŠ polarity, jako je napÄtĂ zdroje. Tuto vlastnost majĂ prĂĄvÄ MOS tranzistory s obohacenĂ˝m kanĂĄlem. Invertor je moĹžnĂŠ realizovat s odporovou zĂĄtÄĹžĂ, jak je znĂĄzornÄno na obr. 7.16.a, avĹĄak z hlediska jednoduchosti technologie vĂ˝roby je mnohem jednoduĹĄĹĄĂ realizovat zĂĄtÄĹž pomocĂ dalĹĄĂho tranzistoru MOS, jehoĹž elektroda G je na pevnĂŠm napÄtĂ UG, kterĂŠ mĹŻĹže bĂ˝t menĹĄĂ nebo rovno napÄtĂ zdroje E. Tato alternativa je na obr. 7.16.b.
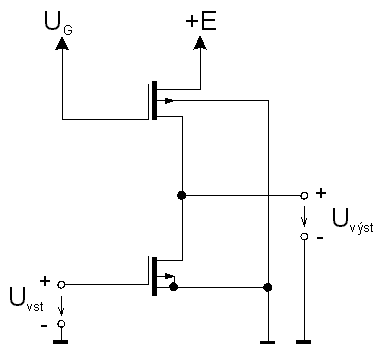
NapĂĄjecĂ napÄtĂ bĂ˝vĂĄ 12 V, coĹž je dĂĄno velikostĂ prahovĂŠho napÄtĂ - okolo 4 V. Aby bylo moĹžno snĂĹžit napĂĄjecĂ napÄtĂ, byla vypracovĂĄna Ĺada technologiĂ, kterĂŠ sniĹžujĂ prahovĂŠ napÄtĂ aĹž na 1.5 - 2V (napĹ. technologie MNOS, kterĂĄ pro izolacĂ G elektrody uĹžĂvĂĄ kombinace vrstev nitridu a kysliÄnĂku kĹemĂku, technologie "silicon gate MOS", kde se pro ovlĂĄdacĂ elektrodu pouĹžĂvĂĄ polykrystalickĂ˝ kĹemĂk obohacenĂ˝ bĂłrem, technologie RMOS s molybdenovou ovlĂĄdacĂ elektrodou apod.). KombinacĂ MOSFETovĂ˝ch spĂnaÄĹŻ je moĹžnĂŠ konstruovat jak hradlo NAND, tak hradlo NOR, jak ukazuje obr. 7.17.a, b.
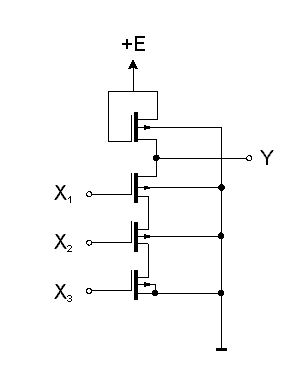
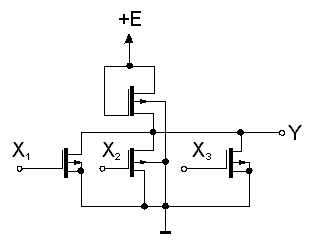
Obvody s tranzistory MOS sice nevyĹžadujĂ k ovlĂĄdĂĄnĂ prakticky ŞådnĂ˝ proud (kromÄ proudu nabĂjejĂcĂho parazitnĂ kapacity mezi ĹĂdicĂ elektrodou a kanĂĄlem), avĹĄak v sepnutĂŠm stavu odebĂrajĂ ze zdroje proud, kterĂ˝ se bezĂşÄelnÄ tratĂ v zĂĄtÄĹži. VĂ˝znamnĂ˝m krokem ke snĂĹženĂ spotĹeby, umoĹžnÄnĂ˝m zejmĂŠna rozvojem technologie vĂ˝roby integrovanĂ˝ch MOSovĂ˝ch obvodĹŻ proto byla moĹžnost realizace tranzistorĹŻ MOS s obohacenĂ˝mi kanĂĄly typu P a typu N na jedinĂŠm Äipu a tĂm i moĹžnost realizace komplementĂĄrnĂch MOSovĂ˝ch obvodĹŻ (CMOS). Invertor CMOS se liĹĄĂ od invertoru typu MOS tĂm, Ĺže jeho zĂĄtÄĹž je tvoĹena MOS tranzistorem opaÄnĂŠ polarity a ĹĂdicĂ elektrody obou tranzistorĹŻ jsou spojeny. PrahovĂĄ napÄtĂ jsou volena tak, aby pĹi vstupnĂm napÄtĂ rovnĂŠm logickĂŠ nule nebo jedniÄce byl vĹždy otevĹen pouze jeden z obou tranzistorĹŻ. Tranzistory tak fungujĂ prakticky jako spĂnaÄe, kterĂŠ pĹipĂnajĂ vĂ˝stup buÄ na napĂĄjecĂ napÄtĂ E, nebo k zemi. Je zĹejmĂŠ, Ĺže pokud nezatÄĹžujeme vĂ˝stup takovĂŠho obvodu, je jeho spotĹeba v klidovĂŠm stavu prakticky nulovĂĄ. VĂ˝stup obvodu mĂĄ relativnÄ velice malou impedanci v obou stavech (ĹĂĄdovÄ stovky ohmĹŻ), coĹž umoĹžĹuje propojovat jednotlivĂĄ pouzdra s obvody bÄĹžnou technikou tiĹĄtÄnĂ˝ch spojĹŻ. Jednoduchost obvodĹŻ je umoĹžĹuje sdruĹžovat ve znaÄnĂŠ hustotÄ na Äipu a vytvĂĄĹet tak obvody velkĂŠ a extrĂŠmnÄ velkĂŠ integrace. NapĹ. operaÄnĂ pamÄti poÄĂtaÄĹŻ se dnes vyrĂĄbÄjĂ tĂŠmÄĹ vĂ˝hradnÄ technologiĂ MOS nebo CMOS (prĹŻmÄrnĂĄ doba vybavenĂ informace z pamÄti MOS je okolo 20-100 ns). RovnÄĹž naprostĂĄ vÄtĹĄina dnes vyrĂĄbÄnĂ˝ch mikroprocesorĹŻ vyuĹžĂvĂĄ systĂŠmu MOS nebo CMOS. Jako pĹĂklad uvĂĄdĂme na obr. 7.18.a,b hradla NAND a NOR v systĂŠmu CMOS.

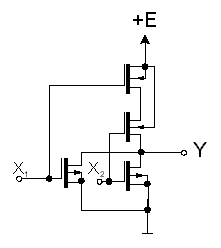
Je tĹeba jeĹĄtÄ poznamenat, Ĺže ve skuteÄnĂ˝ch obvodech MOS a CMOS je nutno chrĂĄnit vstupnĂ elektrodu pĹed prĹŻrazem vysokĂ˝m statickĂ˝m napÄtĂm. NejbÄĹžnÄjĹĄĂ ochrana je pomocĂ Zenerovy diody, kterĂĄ je zapojena mezi substrĂĄt (normĂĄlnÄ uzemnÄnĂ˝) a ĹĂdĂcĂ elektrodu. Tato dioda v normĂĄlnĂm reĹžimu nevede a otevĂrĂĄ se pouze dosĂĄhne-li napÄtĂ na ĹĂdĂcĂ elektrodÄ urÄitĂŠ hodnoty. V integrovanĂŠm obvodu je ochrana nutnĂĄ ovĹĄem pouze pro vstup tÄch hradel, kterĂŠ jsou vyvedeny ven z pouzdra.
V nÄkterĂ˝ch pĹĂpadech pĹi spojovĂĄnĂ vĂ˝stupĹŻ hradel je vĂ˝hodnĂŠ pouĹžĂvat tzv. tĹĂstavovĂ˝ch logickĂ˝ch ÄlenĹŻ, kdy vedle vĂ˝stupnĂch aktivnĂch stavĹŻ na Ăşrovni logickĂŠ nuly a jedniÄky existuje jeĹĄtÄ tĹetĂ stav, kdy vĂ˝stup hradla je v podstatÄ od sbÄrnice odpojen (pĹipojen ke sbÄrnici pĹes velkou impedanci). Tento stav umoĹžĹuje stejnÄ jako hradlo s otevĹenĂ˝m kolektorem pĹipojenĂ vĂ˝stupĹŻ hradel do jednoho bodu. PrincipiĂĄlnĂ zapojenĂ tĹĂstavovĂŠho hradla NAND je na obr. 7.19.
Vedle dvou aktivnĂch vstupĹŻ A a B mĂĄ hradlo blokovacĂ vstup UB. VybuzenĂm tranzistoru T1 se uzavĹou tranzistory T3 aĹž T5 a hradlo mĂĄ velkou vĂ˝stupnĂ impedanci.