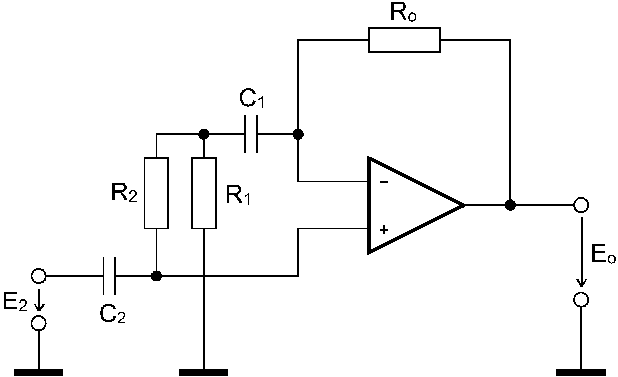
V tĂŠto kapitole si popĂĹĄeme nÄkterĂŠ principiĂĄlnĂ zapojenĂ obvodĹŻ pouĹžĂvanĂ˝ch pĹi analogovĂŠm zpracovĂĄnĂ vĂ˝sledkĹŻ mÄĹenĂ. Jako aktivnĂ prvek se v tÄchto obvodech pouĹžĂvĂĄ zejmĂŠna operaÄnĂ zesilovaÄ v rĹŻznĂ˝ch formĂĄch.
V nĂĄsledujĂcĂch odstavcĂch budou proto popsĂĄny nÄkterĂŠ aplikace operaÄnĂho zesilovaÄe v obvodech pro analogovĂŠ zpracovĂĄnĂ signĂĄlu, jako jsou funkÄnĂ mÄniÄe, obvody pro integraci a derivaci, zĂĄkladnĂ aritmetickĂŠ operace a nÄkterĂĄ dalĹĄĂ pouĹžitĂ operaÄnĂho zesilovaÄe v mÄĹĂcĂ technice.
OperaÄnĂ zesilovaÄ byl pĹŻvodnÄ pouĹžĂvĂĄn jako zĂĄkladnĂ jednotka analogovĂ˝ch poÄĂtaÄĹŻ, diferenciĂĄlnĂch analyzĂĄtorĹŻ. V poslednĂch letech s rozvojem hybridnĂch a pozdÄji monolitickĂ˝ch integrovanĂ˝ch obvodĹŻ se stal operaÄnĂ zesilovaÄ samostatnou jednotkou, elektronickĂ˝m prvkem. OperaÄnĂ zesilovaÄ pouĹžĂvanĂ˝ ve fyzikĂĄlnĂm mÄĹenĂ nemusĂ bĂ˝t ovĹĄem pouze v monolitickĂŠ formÄ, ale mĹŻĹže bĂ˝t buÄ v hybridnĂ formÄ nebo dokonce sestaven z diskrĂŠtnĂch prvkĹŻ.
Vedle pouĹžitĂ operaÄnĂch zesilovaÄĹŻ v analogovĂ˝ch poÄĂtaÄĂch, kde byl hlavnÄ pouĹžĂvĂĄn pro zĂĄkladnĂ aritmetickĂŠ operace seÄĂtĂĄnĂ, odeÄĂtĂĄnĂ, dÄlenĂ a nĂĄsobenĂ a rovnÄĹž pro integraci analogovĂ˝ch signĂĄlĹŻ, se dnes pouĹžĂvĂĄ i v ĹadÄ elektronickĂ˝ch obvodĹŻ jako jsou stejnosmÄrnĂŠ i stĹĂdavĂŠ zesilovaÄe, komparĂĄtory, elektronickĂ˝ vzorkovacĂ obvod (vrĂĄtka, gate), klopnĂŠ obvody, aktivnĂ filtry, pĹevodnĂky z analogovĂŠho signĂĄlu na ÄĂselnou hodnotu a naopak.
V tĂŠto kapitole vzhledem k vĹĄestrannĂŠmu pouĹžitĂ operaÄnĂch zesilovaÄĹŻ budou podĂĄny jeho zĂĄkladnĂ vlastnosti s ohledem na jeho moĹžnĂŠ fyzikĂĄlnĂ aplikace.
OperaÄnĂ zesilovaÄ je v podstatÄ ĹĄirokopĂĄsmovĂ˝ zesilovaÄ se stejnosmÄrnĂ˝m vstupem, s velkĂ˝m vstupnĂm odporem Ri ĹĂĄdu stovky kW aĹž nÄkolika MW , s malĂ˝m vĂ˝stupnĂm odporem ĹĂĄdu 100 W a velkĂ˝m zesĂlenĂm vÄtĹĄĂm neĹž 104.
Jeho schematickĂĄ znaÄka je na obr. 5.1.
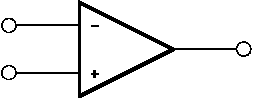
OperaÄnĂ zesilovaÄ mĂĄ dva vstupnĂ obvody: invertujĂcĂ a neinvertujĂcĂ. PĹi zavedenĂ signĂĄlu na invertujĂcĂ vstup se na vĂ˝stupu operaÄnĂho zesilovaÄe objevĂ signĂĄl v opaÄnĂŠ fĂĄzi, zatĂmco pĹi pĹivedenĂ signĂĄlu na neinvertujĂcĂ vstup je signĂĄl na vstupu a vĂ˝stupu operaÄnĂho zesilovaÄe ve fĂĄzi.
Pro dalĹĄĂ Ăşvahy si pro jednoduchost zaveÄme pojem ideĂĄlnĂho operaÄnĂho zesilovaÄe, jehoĹž parametry definujeme takto:
ZesĂlenĂ zesilovaÄe A a vstupnĂ odpor Ri jsou nekoneÄnÄ velkĂŠ. VĂ˝stupnĂ odpor Rv je nulovĂ˝. PĹedpoklĂĄdĂĄ se, Ĺže ideĂĄlnĂ operaÄnĂ zesilovaÄ nemĂĄ ofset ani drift. Ofsetem rozumĂme nenulovĂ˝ vĂ˝stupnĂ signĂĄl pĹi zkratovanĂ˝ch a uzemnÄnĂ˝ch vstupnĂch svorkĂĄch a driftem zmÄnu ofsetu s Äasem a teplotou. RovnÄĹž vliv souÄtovĂŠho signĂĄlu je nulovĂ˝, tj. Äinitel potlaÄenĂ souÄtovĂŠho signĂĄlu H ÂŽ Ä. IdeĂĄlnĂ operaÄnĂ zesilovaÄ zesiluje rovnÄĹž rovnomÄrnÄ signĂĄly vĹĄech frekvencĂ vÄetnÄ nulovĂŠ; je to tedy stejnosmÄrnÄ vĂĄzanĂ˝ zesilovaÄ. VĹĄechny uvedenĂŠ veliÄiny a pojmy budou probrĂĄny postupnÄ v tĂŠto kapitole; zde jsou uvedeny jedinÄ z dĹŻvodĹŻ ĂşplnĂŠ definice ideĂĄlnĂho operaÄnĂho zesilovaÄe.
NejdĹĂve si vybudujeme teorii ideĂĄlnĂho operaÄnĂho zesilovaÄe a pak si ukĂĄĹžeme na nÄkterĂŠ odchylky, kterĂŠ jsou zpĹŻsobeny odchylkami parametrĹŻ reĂĄlnĂŠho operaÄnĂho zesilovaÄe od zesilovaÄe ideĂĄlnĂho. Jako zesilovaÄ s velkĂ˝m zesĂlenĂm nenĂ operaÄnĂ zesilovaÄ prakticky pouĹžitelnĂ˝ bez zĂĄpornĂŠ zpÄtnĂŠ vazby. Teorie ideĂĄlnĂho operaÄnĂho zesilovaÄe je tak v podstatÄ teoriĂ jeho zpÄtnĂŠ vazby.
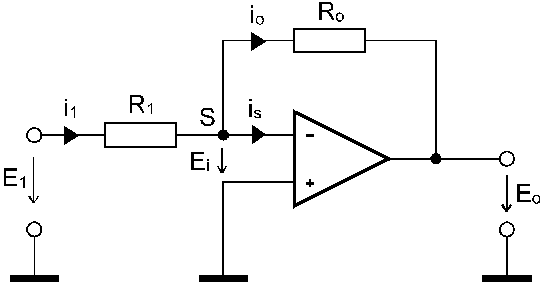
ZapojenĂ zpÄtnĂŠ vazby s invertujĂcĂm vstupem je na obr.5.2.a. Z obr. 5.2.a. je patrno, Ĺže pro proudy is, i1 a i0 platĂ vĂ˝razy:
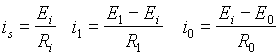 .
.
Pro ideĂĄlnĂ operaÄnĂ zesilovaÄ je Ri ÂŽ Ä ; pak is = 0 a i1 = io.
Pak 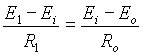 , (5.1)
, (5.1)
kde 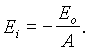
U ideĂĄlnĂho operaÄnĂho zesilovaÄe vzhledem k tomu, Ĺže |A| ÂŽ Y , je Ei ÂŽ 0 a
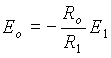 .
.
ObdobnÄ s pomocĂ operĂĄtorĹŻ mĹŻĹžeme psĂĄt pro obecnĂŠ impedance Z0(p) a Z1(p)
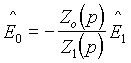 . (5.2)
. (5.2)
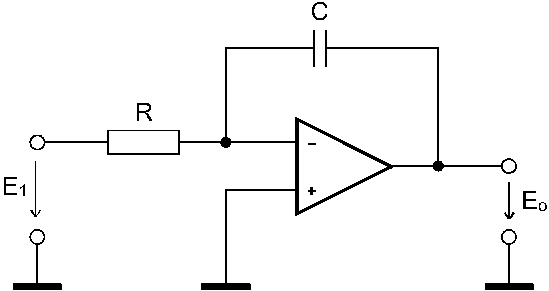
Jako pĹĂklad pro pouĹžitĂ vztahu (5.2) probereme integraÄnĂ obvod, jehoĹž zĂĄkladnĂ zapojenĂ je patrno na obr. 5.2.b.
Z obr. 5.2.b plyne, Ĺže operĂĄtorovĂŠ impedance
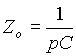 a
a ![]() ;
;
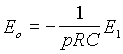
a originål je dån výrazem
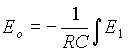 dt
dt
VstupnĂ impedanci Zvstup pro zapojenĂ operaÄnĂho zesilovaÄe se zpÄtnou vazbou s invertujĂcĂm vstupem vypoÄĂtĂĄme tak, Ĺže nejdĹĂve vypoÄteme impedanci v souÄtovĂŠm bodÄ S.
U ideĂĄlnĂho OZ je Rs ÂŽ 0 vzhledem k tomu, Ĺže | A |ÂŽ Ä. VstupnĂ impedance se blĂŞà R1, Zvstup Ž R1. ObraĹĽme nynĂ pozornost na zapojenĂ s neinvertujĂcĂm vstupem.
Schematicky je zapojenĂ patrno na obr. 5.3. ObdobnĂ˝m zpĹŻsobem jako v pĹĂpadÄ neinvertujĂcĂho vstupu obdrĹžĂme:
![]()
Pro ideĂĄlnĂ zesilovaÄ opÄt vzhledem k tomu, ze |A| ÂŽ Ä je Ei ÂŽ 0 a tedy
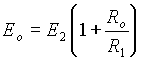
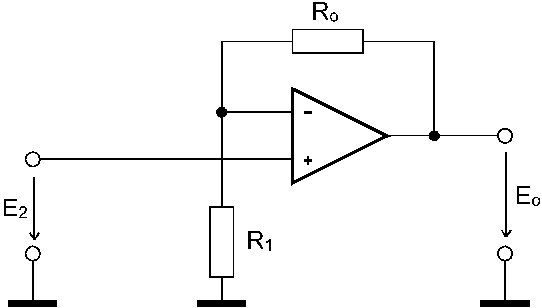
VstupnĂ impedance pro zapojenĂ s neinvertujĂcĂm vstupem je velmi vysokĂĄ, Zvstup Ž Â Ä . PĹejdÄme nynĂ z ideĂĄlnĂho operaÄnĂho zesilovaÄe na pĹĂpad reĂĄlnĂ˝, kdy Ri, Rv, A majĂ koneÄnĂŠ hodnoty. DĂĄle je nutnĂŠ u reĂĄlnĂŠho operaÄnĂho zesilovaÄe uvaĹžovat jeho drift, ofset, vliv souÄtovĂŠho signĂĄlu a frekvenÄnĂ charakteristiku. V dalĹĄĂm budou proto postupnÄ probrĂĄny nÄkterĂŠ zmÄny zpĹŻsobenĂŠ odchylkami parametrĹŻ reĂĄlnĂŠho operaÄnĂho zesilovaÄe od ideĂĄlnĂho.
V pĹĂpadÄ, Ĺže Ri je koneÄnĂŠ, nelze proud tekoucĂ vstupem zesilovaÄe is zanedbat a vĂ˝raz (5.1) pĹejde ve vztah
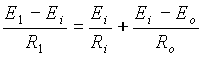 (5.4)
(5.4)
Vezmeme-li v Ăşvahu, Ĺže E0 = - A.Ei, dostaneme po ĂşpravÄ vĂ˝raz:
![]()
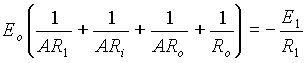
takĹže:
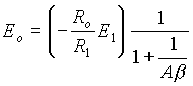 (5.5)
(5.5)
kde faktor b je dån výrazem
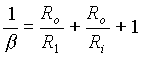
VypoÄteme si napÄtĂ vytvoĹenĂŠ na vstupu operaÄnĂho zesilovaÄe Ei jestliĹže uvaĹžujeme obvod zpÄtnĂŠ vazby jako dÄliÄ. JestliĹže uvaĹžujeme i vstupnĂ odpor operaÄnĂho zesilovaÄe Ri dostaneme:
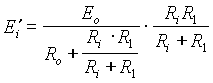
![]()
Odtud vypoÄteme pomÄr napÄtĂ
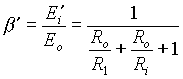
tj. ![]() ,
,
koeficient b je tedy koeficientem dÄliÄe vytvoĹenĂŠho zpÄtnou vazbou. Je tedy
E0 = (vztah pro ideĂĄlnĂ OZ). 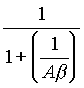 ,
,
kde A je zesĂlenĂ zesilovaÄe a b je koeficient zpÄtnĂŠ vazby z vĂ˝stupu na vstup zesilovaÄe. JestliĹže vezmeme v Ăşvahu i vĂ˝stupnĂ odpor operaÄnĂho zesilovaÄe Rv a zatÄĹžovacĂ odpor RL zesilovaÄe dostaneme
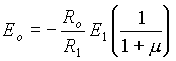 ,
,
kde
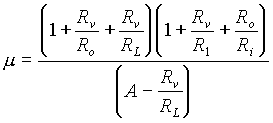
pro m < < 1 platĂ
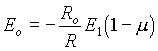
VeliÄina m pĹedstavuje chybu pĹi zesĂlenĂ u reĂĄlnĂŠho operaÄnĂho zesilovaÄe. Jako pĹĂklad si uvedeme operaÄnĂ zesilovaÄ majĂcĂ tyto parametry: A = 105, Ri = 100 kW , Rv = 100 W .Hodnoty obvodovĂ˝ch prvkĹŻ: R1=10 kW , Ro= 10kW , RL = 10 kW. tj. relativnĂ chyba vzhledem k ideĂĄlnĂmu operaÄnĂmu zesilovaÄi je e r = 0,12 %.
VstupnĂ impedance Z vstup zapojenĂ OZ s invertujĂcĂm vstupem je dĂĄna vĂ˝razem (srovnej se vztahem (5.3)).
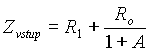 ; (5.6)
; (5.6)
odhadnÄme velikost druhĂŠho Älenu na pravĂŠ stranÄ vĂ˝razu (5.6). Pro typickĂŠ zapojenĂ, kde zpÄtnovazebnĂ odpor je Ro ~ 104 - 105 W a zesĂlenĂ A ~ 104 - 106 pak platĂ
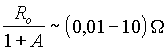 .
.
To znamenĂĄ, Ĺže prakticky lze druhĂ˝ Älen na pravĂŠ stranÄ vĂ˝razu (5.6) ve vÄtĹĄinÄ pĹĂpadĹŻ zanedbat a vstupnĂ impedance je urÄena odporem (resp. impedancĂ) R1 (resp.Z1) jako v pĹĂpadÄ ideĂĄlnĂho operaÄnĂho zesilovaÄe.
DynamickĂ˝ vstupnĂ odpor Rvstup v zapojenĂ s neinvertujĂcĂm vstupem u reĂĄlnĂŠho operaÄnĂho zesilovaÄe vypoÄteme ze zmÄny napÄtĂ o D E2 zmÄny vstupnĂho proudu D J vstup ze vztahu
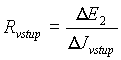 .
.
UrÄĂme nejprve D Jvstup . ZmÄna vĂ˝stupnĂho napÄtĂ D Eo , kterĂĄ je vyvolanĂĄ zmÄnou vstupnĂho napÄtĂ o D Ei:
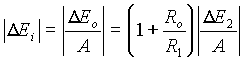
zmÄna D Jvstup je pak dĂĄna vztahem
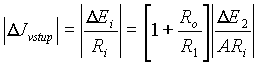
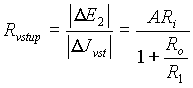 (5.7)
(5.7)
Jako pĹĂklad uvedeme zesilovaÄ, kterĂ˝ mĂĄ zesĂlenĂ se zpÄtnou vazbou rovnĂŠ 100, A ~  104, Ri ~  40 kW .
Pak ![]() ~
100
~
100
a ze vztahu (5.7) plyne, Ĺže dynamickĂ˝ vstupnĂ odpor reĂĄlnĂŠho operaÄnĂho zesilovaÄe v zapojenĂ s neinvertujĂcĂm vstupem je
Rvstup ~ 4 MW .
JestliĹže je tĹeba jeĹĄtÄ zvýťit vstupnĂ odpor neinvertujĂcĂho vstupu, je moĹžnĂŠ uĹžĂt zapojenĂ znĂĄmĂŠ pod nĂĄzvem âbootstrappingâ. PrincipiĂĄlnĂ zapojenĂ je patrno z obr. 5.4. Metoda spoÄĂvĂĄ v tom, Ĺže ÄĂĄst vĂ˝stupnĂho signĂĄlu vedeme ve stejnĂŠ polaritÄ na neinvertujĂcĂ vstup, ÄĂmĹž hradĂme ÄĂĄst proudu na vstup zesilovaÄe, tj. zavĂĄdĂ se slabĂĄ kladnĂĄ zpÄtnĂĄ vazba. KladnĂĄ zpÄtnĂĄ vazba mĂĄ za nĂĄsledek, Ĺže proud na vstupu operaÄnĂho zesilovaÄe poklesne a. vstupnĂ odpor Rvstup se zvýťĂ.