2.1. Měření napětí a proudu

Jedním ze základních elektrických měřicích přístrojů na školách jsou a asi ještě nějakou dobu zůstanou deprézské měřicí přístroje, tj. přístroje s otočnou cívkou. Před všemi digitálními multimetry mají totiž jednu velikou přednost - nepotřebují ke svým základním činnostem, tj. k měření napětí nebo proudu baterie nebo připojení na rozvodnou síť (přívlastek ”rozvodnou” nesmíme dnes, v době počítačových sítí, již opomínat). Navíc si v současné době i výrobci číslicových ručních přístrojů uvědomují přednosti analogové indikace a vybavují své číslicové multimetry navíc analogovým sloupcovým displejem. Věnujme se proto chvíli deprézským měřicím přístrojům. Výchylka ručičky deprézského přístroje je úměrná proudu, který protéká otočnou cívkou, a sice první mocnině tohoto proudu. Je tedy třeba si uvědomit, že i při měření napětí musí měřený zdroj dodat do otočné cívky proud, aby způsobil její vychýlení. Proud protékající otočnou cívkou na plnou výchylku přístroje je jednou ze základních charakteristik deprézského přístroje. Tento proud zjistíme nejsnáze tak, že se podíváme na nejcitlivější stejnosměrný proudový rozsah přístroje (pokud se jedná o universální, tedy vícerozsahový přístroj). U běžných přístrojů bývá 1 mA, u citlivých systémů 20 nebo dokonce jen 10 μA. Vyjadřuje se v kΩ/V. 1 kΩ/V znamená tedy přístroj s proudem 1mA na plnou výchylku, 50 kΩ/V přístroj se spotřebou 20 μA a 100kΩ/V přístroj se spotřebou 10 μA (údaj v kΩ/V má tedy rozměr A^-1 a znamená vlastně počet výchylek na 1 A, například 100kΩ/V znamená 10⁵ výchylek na 1A, tj. na jednu výchylku 10^-5A). Uvědomme si, že údaj např. 50kΩ/V nám nic neříká o vlastním vnitřním odporu měřicího systému, ten bývá v řádu jednotek kΩ, to znamená, že na plnou výchylku na přístroji se spotřebou 20 μA na plnou výchylku zůstává napětí řekněme okolo 0,1 V. Z údaje v kΩ/V však můžeme spočítat vnitřní odpor deprézského přístroje jako celku (tj. i se sériovými odpory), je-li použit jako voltmetr. Je-li například údaj 50kΩ/V a měříme na rozsahu 10V, pak sériový odpor k otočné cívce přístroje je spočítán tak, aby celkový odpor měřicího přístroje byl 500 kΩ a obdobně na jiných rozsazích. Předpokládám, že by pro nikoho nebyl problém spočítat tento sériový odpor, když by byl znám proud na plnou výchylku I_P a vnitřní odpor měřicího systému R_M. Zkusme si to: Mějme určit sériový odpor R_S pro deprézský systém na rozsahu U_R a známe I_P a R_M. Znamená to, že při přiložení napětí U_R musí přístroj ukázat plnou výchylku, tj. systémem musí protékat proud I_P. Z Ohmova zákona tedy R_S = - R_M+(U_R/I_P).

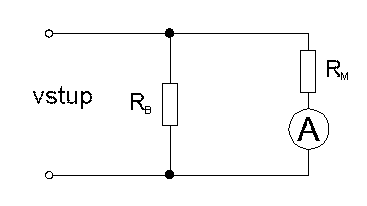
Při použití deprézského systému jako ampérmetru musíme pro měření proudů větších než je proud na plnou výchylku I_p použít bočníku, tj. odporu zapojeného paralelně s měřicím systémem. Existuje i tzv. Ayrtonův bočník, který si můžeme představit jako potenciometr připojený paralelně k měřicímu systému, oba typy bočníků představuje obrázek 2.1.

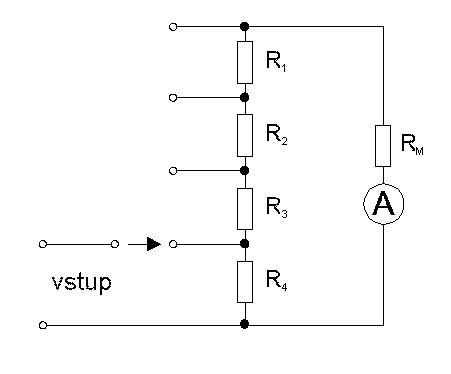
obr. 2.1

Zde předvedeme výpočet odporu R_B pouze jednoduchého bočníku, Ayrtonův si můžete spočítat jako domácí cvičení. Předpokládáme parametry systému dané stejnými symboly jako nahoře, proudový rozsah, pro který bočník počítáme, označme I_R.
Proud I tekoucí do uzlu bočník, měřicí systém, se bude větvit na dvě části, které dohromady podle 1. Kirchhoffova zákona musí dát celkový měřený proud. Část protékající měřicím systémem bude rovna pro plnou výchylku I_P, tedy

I_P=I_RR_B/R_M=I.R_B/(R_M+R_B). 

I_P,I_R a R_M známe, jedinou neznámou v této rovnici je odpor bočníku R_B. Všimněte si, že v případě tohoto jednoduchého bočníku bude spád napětí na přístroji s bočníkem stejný jako na samotném měřicím systému, tj. R_M.I_P. To u Ayrtonova bočníku nebude platit, tam bude pro vyšší proudové rozsahy spád napětí na kombinaci vyšší, než je na systému. Pro vysoké proudové rozsahy vycházejí odpory bočníků velmi malé a má-li mít přístroj přepínané rozsahy, vzniká problém s přechodovým odporem přepínače, který může být srovnatelný s odporem bočníku. Proto řada univerzálních měřicích přístrojů má pro vyšší proudový rozsah, např. 10 A, zvláštní připojovací zdířku, aby se tomuto problému předešlo.

Zatím jsme se zabývali konstrukcí měřicího přístroje s deprézským systémem. Předpokládejme nyní, že máme k dispozici buď deprézský nebo jakýkoli jiný měřicí přístroj, známe jeho vnitřní odpory pro měření proudu a pro měření napětí a chceme určité měření provést. Je třeba si uvědomit, že každým měřením ovlivňujeme měřený obvod, že měřením vlastně měníme měřený obvod na obvod obsahující původní obvod a měřicí přístroj. Tato změna může v řadě případů způsobit jen malou chybu, ale v některých případech je třeba analýzu ovlivňování měřeného obvodu měřicím přístrojem provést. Předpokládejme nejprve měření proudu ampérmetrem s vnitřním odporem R_A v jednoduchém obvodu složeném ze zdroje napětí E s vnitřním odporem R_i a jednoho rezistoru s odporem R_L, viz obrázek 2.2.

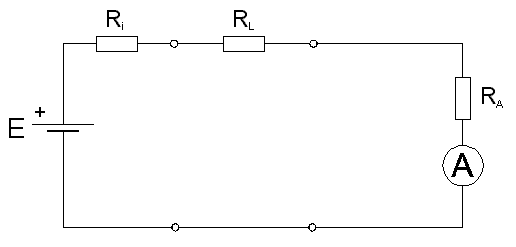
obr. 2.2

Podle Ohmova zákona je zřejmé, že proud protékající obvodem bude dán podílem napětí E a součtu všech tří odporů, I=E/(R_i+R_L+R_A). Nebude-li tedy R_A « R_i + R_L, naměříme jiný proud, než ten, který by protékal rezistorem s odporem R_L bez připojeného ampérmetru. Mějme na paměti, že moderní digitální multimetry nejsou v tomto směru žádnou výjimkou, mají též svůj vnitřní odpor a též ovlivňují měřený obvod. Obdobně je tomu při měření napětí. Předpokládejme stejný měřený obvod, složený ze zdroje o napětí E a vnitřním odporu R_i, zapojeného na rezistor s odporem R_L a předpokládejme nyní, že chceme změřit napětí na rezistoru R_L voltmetrem s vnitřním odporem R_V, viz obrázek 2.3.

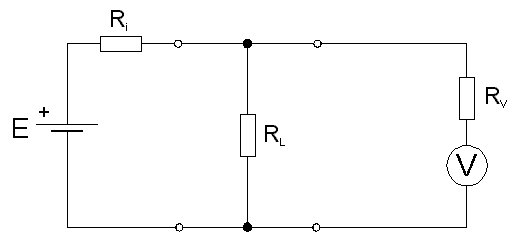
obr 2.3

K tomu, abychom vypočítali, jaké napětí vlastně naměříme (v tomto a v předchozím příkladu se nezabýváme vůbec přesností měření, tedy odečtu na měřicím přístroji, předpokládáme prostě, že jsme z výchylky nebo údaje na displeji schopni přesně stanovit napětí, jaké je na voltmetr přiloženo, nebo proud, který ampérmetrem protéká), nahraďme obvod se zdrojem E, vnitřním odporem R_i a rezistorem R_L Théveninovým ekvivalentem se zdrojem E’=E.R_L/(R_i+R_L) a vnitřním odporem R_i’ = R_iR_L/(R_i+R_L). Tento zdroj bude tedy napájet náš voltmetr s vnitřním odporem R_V a tedy na voltmetru bude napětí U_V=E’. R_V/(R_i’+R_V). Přitom napětí E’ je to napětí, které chceme měřit, tedy napětí na rezistoru R_L bez připojeného voltmetru. Jedině tedy v případě, že odpor voltmetru R_v » R_i’ můžeme očekávat, že naměřené napětí bude rovné předpokládanému, jinak bude relativní chyba δE’/E’ vzniklá připojením voltmetru zhruba rovna δE’/E’ ≈ -R_i’/R_V, tj. naměříme napětí menší než je skutečné. Uvedený jednoduchý vzorec pro chybu měření platí jen pro poměr R_i’/R_V << 1, jinak je nutné použít přesný vzorec uvedený výše. Jednoduchou úvahou s využitím vnitřního odporu voltmetru můžeme rozšířit i měřicí rozsah voltmetru, např. je-li měřicí rozsah voltmetru V_R voltů a vnitřní odpor 10 MΩ, pak připojením rezistoru o odporu 40 MΩ do série s voltmetrem získáme voltmetr s rozsahem 5.V_R. (Pozor na bezpečnost a na úraz elektrickým proudem, rezistor 40 MΩ musí vydržet napětí 4.V_R !)

Než začneme probírat měření odporu, řekněme si něco o rozvodu elektrické energie. Bývá zvykem, že absolventi gymnasia, pokud se o tuto problematiku sami nezajímají, nemají v této otázce příliš jasno, i když se jedná, např. při přípravě pokusů, o jejich bezpečnost. Třífázové elektrické napětí vyrobené v elektrárně (mimochodem, víte, že napětí generované v elektrárně má efektivní hodnotu cca 25 kV?) se transformuje nahoru, aby se zmenšily ohmické ztráty ve vedení při přenosu energie (kolikrát zvýším napětí, tolikrát zmenším proud a ohmické ztráty jsou úměrné protékajícímu proudu). Při velmi vysokém napětí však dochází vlivem elektrického pole v okolí vodičů vysokého napětí k průrazu vzduchu, obklopujícího vedení, vzduch se ionizuje a vzniká vodivý kanál např. k uzemňovacímu vedení nebo k uzemněnému stožáru (jistě si vzpomínáte, když jste byli v mlze v blízkosti vedení vysokého napětí na zvuky, které toto vedení vydává - jsou to zvuky vyvolané krátkými průrazy vzduchu). Aby se tyto ztráty sršením zmenšily na minimum, vyrábí se vysokonapěťové vedení ve formě dvou nebo tří nebo i více vodičů pro jednu fázi paralelně, jejichž vzdálenost je udržována distančními vložkami. Je to proto, aby se zvětšil efektivní průměr vedení a elektrické pole v okolí vedení, které je nepřímo úměrné tomuto efektivnímu průměru, se zmenšilo. Rozvod velmi vysokým napětím se používá jen na velké vzdálenosti, pro danou oblast se napětí snižuje na 22 kV a ty se rozvádějí do jednotlivých lokalit, které mají dále své transformátory na převod dolů na napětí 380/220V. Takový transformátor mají i jednotlivé provozy, které spotřebovávají větší množství elektrické energie. V současné době se připravuje v rámci evropské integrace přechod na rozvodnou soustavu 400/230 V. Rozvod napětí 380/220V v městě se provádí většinou kabelem v zemi, v menších obcích i vrchním vedením. V přípojné skříni k objektu se vedení jistí proti možnému zkratu tzv. nožovými pojistkami s hodnotou jištěného proudu cca 100A a po příchodu do objektu ještě jednou, pro rodinný domek je typická hodnota 35A na fázi. Takto jištěné vedení vede do domovní rozvodné skříně, kde se jistí již automatickým jističem s hodnotou proudu zpravidla 25A, následuje elektroměr a obvody jednotlivých místností, kde se typicky jistí zvlášť světelné obvody jističem 6A a zásuvkové obvody jističem 10A. Pouze speciální zásuvky, kde se předpokládá vyšší spotřeba, např. u automatické pračky (topení, nikoli motor), se jistí jističi 16A. Jistič, jak víte, má dva vypínací mechanismy, jeden elektromagnetický pro rychlé vypnutí v případě zkratu (podle normy by měl vypnout do 0,4 s), jeden bimetalový pro odpojení v případě trvalého přetížení na cca 140%. Jističe jistí vedení ke světlu, případně k zásuvkám, které pak může mít menší průřez použitého vodiče, nikoliv tedy připojené spotřebiče, ty by měly mít (a ve velké většině také mají) svou ochranu tavnou nebo tepelnou pojistkou apod. Údaj uvedený na zásuvce, např. 220V/16A nemusí vůbec souviset s napětím, na které je zásuvka připojena a proudem, na které je vedení jištěno, jsou to pouze maximální hodnoty napětí a proudu, při kterých může být zásuvka použita. Zásuvky jsou, ovšem, typizované a podle platných norem by se měly použít jen na nominální tedy jmenovité napětí, vy ale budete muset pracovat v reálném prostředí, kde se můžete s odchylkami setkat. Protože se ještě i dnes můžete setkat s rozvodem 120V, je důležité se informovat před zapojením spotřebiče, jaké je nominální napětí v síti, a přesvědčit se, že spotřebič je na toto napětí vyroben, případně nastaven.

Přejděme nyní k měření odporů. Základní metodou měření odporů je metoda přímá, tj. metoda založená na Ohmově zákoně. Změříme-li tedy napětí na neznámém rezistoru a současně proud tímto rezistorem, můžeme vypočítat odpor rezistoru z Ohmova zákona jako poměr napětí na odporu a proudu tímto odporem. Používáme tedy dva měřicí přístroje, jeden na napětí, druhý na proud. A hned tu máme komplikaci: přístroje jdou k měřenému rezistoru zapojit dvěma způsoby, viz obrázek 2.4!

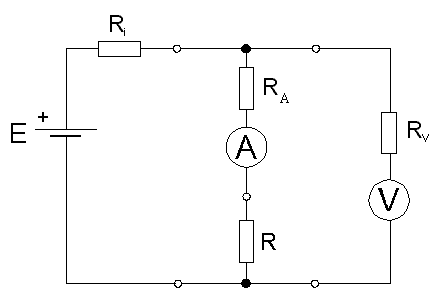
obr. 2.4a

Výběr mezi těmito dvěma možnostmi závisí na vzájemném vztahu vnitřních odporů přístrojů a odporu měřeného obvodu, jak ukážeme tímto způsobem. Předpokládejme nejprve obvod podle obrázku 2.4a. Napětí na sériové kombinaci ampérmetru a měřeného odporu je rovno podle 2. Kirchhoffova zákona V=A.R + A.R_A, kde V a A jsou údaje přečtené (opět s absolutní přesností) na voltmetru a ampérmetru. Neznámá hodnota odporu R je tedy dána jako R=V/A-R_A což znamená, že skutečná hodnota odporu R je menší, než ta, která vychází z naměřeného poměru V/A. Zapojíme-li ampérmetr tak, aby měřil proud voltmetrem a měřeným odporem R, dostaneme vztah

V=A.R_V.R/(R_V +R)

z čehož

R=(V/A).(1-(V/A)/R_V)^-1.

Je-li tedy odpor ampérmetru mnohem menší než naměřené V/A, je vhodnější první metoda, je-li odpor voltmetru mnohem větší, než naměřené V/A, je vhodnější druhá metoda, jsou-li splněny obě podmínky, můžeme si vybrat. V každém případě je pak hledaný odpor roven s dostatečnou přesností naměřenému poměru V/A.

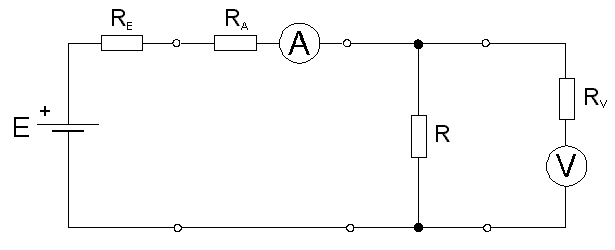
obr. 2.4b

Uvedený způsob nepočítá s odporem připojovacích vodičů. Pro zvlášť malé odpory, nebo pro větší proudy použité při měření, je třeba proto metodu na obrázku 2.4b modifikovat tak, jak je znázorněno na obrázku 2.5.

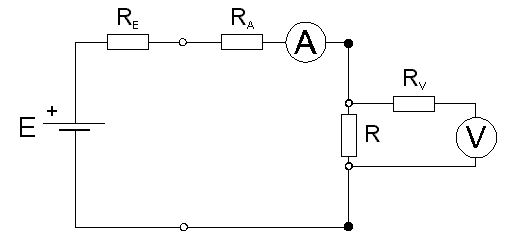
obr. 2.5

Říká se tomu čtyřvodičová metoda měření odporů a vidíme, že se liší od obrázku 2.4b jen tím, že voltmetr je k měřenému rezistoru připojen zvláštními dvěma vodiči, které vedou přímo na vývody rezistoru. Zdá se to být zbytečné, ale měříme-li například rezistor o odporu 10^-2 Ω pomocí vodičů majících každý 0,1 Ω, pak se dostaneme při použití metody na obrázku 2.4b do problémů, protože změřený poměr V/A bude závislý na tom, do jakého místa v obvodu voltmetr připojíme a je velmi pravděpodobné, že naměříme místo odporu rezistoru odpor vodičů. V zapojení čtyřdrátovém (anglicky four wire method) tento problém odpadá.

Při měření odporů přímou metodou si musíme uvědomit, že měřeným odporem prochází proud a že na něm je určité napětí (u přenosných ohmmetrů je to většinou napětí použité baterie, případně je toto napětí na svorkách přístroje vyhrazených pro měření odporů vyznačeno). Může se stát, že odpor prvku, který měříme, je závislý na napětí nebo procházejícím proudu, a tehdy naměřená hodnota bude správná jen pro použitý proud a napětí. Někdy také může být použitý proud pro součástku fatální, nesmíme např. proudem 100mA měřit odpor pojistky, jejíž vypínací hodnota je 50 mA. Je například zvykem měřit pomocí ohmmetru polovodičové diody, zda v propustném směru vedou a v závěrném nikoliv. V tom případě naměříme při různých rozsazích ohmmetru různé odpory diody v propustném směru, neboť různé rozsahy ohmmetru používají různý proud měřeným rezistorem a protože charakteristika diody je (teoreticky) exponenciální, bude se její diferenciální odpor s protékajícím proudem měnit. Na druhé straně budeme-li chtít tímto způsobem otestovat vysokonapěťovou diodu, která se obvykle skládá z několika diod zapojených do série, zjistíme, že ani při jedné polaritě dioda nepovede; přiložené napětí je totiž příliš malé, aby diodu (resp. sérii diod) otevřelo. A tak, ač se to zdá být to nejsložitější, co mohu poradit, nezbývá, než se zamyslet před tím, než přiložím konce drátů vedoucích k přístroji, do měřeného obvodu. Mohli bychom parafrázovat české přísloví na: ”Dvakrát se rozmysli a potom měř”.

Můstkovými metodami měření odporů se nebudeme zabývat, neboť naprostá většina přenosných ohmmetrů pracuje na principu přímé metody. Předpokládám, že každý by uměl nakreslit Wheatstoneův můstek, odvodit rovnici pro rovnováhu v něm a spočítat proud galvanometrem v nevyváženém Wheatstoneově můstku. Jedná se o vztahy buď probírané na střední škole, nebo požadované k přijímacím zkouškám na MFF. Doporučuji každému, kdo to s kantorováním na středních školách myslí vážně, aby si tento můstek spočítal a ubezpečil se tak, nikoliv, že zná příslušné vztahy nazpaměť (v učení se vztahů nazpaměť vynikají především, dámy prominou, posluchačky, ale skutečně to není to pravé), ale že je schopen můstek nakreslit a pomocí některé z metod analýzy obvodů jej vyřešit. Zájemce o další stejnosměrné můstky (Thomsonův dvojmost apod.) odkazuji na literaturu.

Kromě měření napětí pomocí různých analogových či číslicových měřicích přístrojů existují ještě metody kompenzační. V těchto metodách se měřené napětí srovnává s napětím z potenciometru, které se získává z přesného zdroje referenčního napětí tak dlouho, až galvanometr (to není nic jiného, než deprézský systém), spojený mezi měřené a srovnávací napětí, ukáže nulovou výchylku. Tyto kompenzační metody se deklarují jako metody měření napětí bez spotřeby, ve skutečnosti závisí na citlivosti galvanometru, jak dalece ”bez spotřeby” metoda bude, tj. s jakou přesností jsme schopni pomocí galvanometru určit, že protékající proud je roven nule. V současné době, kdy existují operační zesilovače schopné měřit proud v řádu 0,1 pA, jsme již schopni elektronicky ”odsledovat” a tedy měřit napětí s uvedenou spotřebou, tj. spotřebou o cca dva řády nižší, než bychom mohli ”vynulovat” kompenzátor opatřený zrcátkovým galvanometrem. Možná vás to překvapilo, že naši předkové vymysleli v deprézském přístroji tak citlivé měřidlo; se zrcátkovými galvanometry je možná citlivost v řádu 10^-11 A/dílek.

Doposud jsme se zabývali měřeními ve stejnosměrných obvodech. V obvodech střídavého proudu, nebo obecněji v obvodech s časově proměnným proudem, nacházíme kromě rezistorů také kondenzátory a indukčnosti. Jak je to s měřením velikostí kapacit a indukčností? Opět pomineme můstkové metody, jichž existuje celá řada, Maxwellův můstek, Scheringův můstek, Wienův můstek, a soustředíme se na tzv. rezonanční metody, tj. metody, využívající k měření indukčností a kapacit rezonančního obvodu LC a měří se kvalita a rezonanční kmitočet tohoto obvodu. Přístroj k tomuto měření potřebný se jmenuje Q-metr a je to vlastně generátor střídavého napětí o proměnném kmitočtu spojený se střídavým voltmetrem, kterým se měří napětí na kondenzátoru. Vzpomenete-li si na sériový rezonanční obvod probíraný v přednášce z elektřiny a magnetismu, víte, že u sériového rezonančního obvodu rozlišujeme obecně mezi proudovou a napěťovou rezonancí a že frekvence napěťové rezonance se přibližně rovná frekvenci proudové rezonance (určené Thomsonovým vztahem ω_o=(LC)^-1/2) za předpokladu, že činitel jakosti obvodu je velký. Za této podmínky můžeme také určit jakost rezonančního obvodu (Q = ω_rL / R) z tzv. činitele přepětí, Q = U_r / U, kde U_r je napětí na kondenzátoru při rezonanci a U je budicí napětí na celém rezonančním obvodu. (Pokud to nevíte, nezbývá, než se podívat do učebnice, například J. Brož, Základy fyzikálních měření.) V Q-metru je napětí U stabilizováno a napětí U_r se měří střídavým voltmetrem; současně známe nastavenou frekvenci generátoru. Kondenzátory měříme buď tzv. substituční metodou, kdy nastavíme rezonanci s neznámým kondenzátorem, pak jej vyměníme za známý a proměnný a ten měníme tak dlouho, až nastane znova rezonance při jinak konstantních parametrech; pak je nastavená kapacita rovna neznámé kapacitě. Obdobná je metoda diferenční, kdy měrný kondenzátor je v obou případech připojen ke Q-metru; jednou s neznámým kondenzátorem, jednou bez něj. Pak je neznámá kapacita rovna rozdílu kapacity měrného kondenzátoru v obou případech. U indukčností je postup obdobný, jen si musíme uvědomit, že cívku nelze navinout tak, aby neměla kapacitu mezi závity. Označme tuto kapacitu C_o. K tomu, abychom zjistili indukčnost L dané cívky, která má kapacitu vinutí rovnou C_o, potřebujeme dva kondenzátory o známé a různé kapacitě, C₁, C₂. Zjistíme-li rezonanční frekvence kombinace cívka a kondenzátor pro oba kondenzátory C₁ a C₂ a označíme-li je ω₁ a ω₂, platí pak

ω₁²=((C_o+C₁)L)^-1, ω₂²=((C_o+C₁)L)^-1.

Z těchto dvou rovnic můžeme pak spočítat jak vlastní kapacitu cívky, C_o, tak její indukčnost L.

Velmi jednoduchá metoda měření kapacit se zakládá na použití kapacity C v integrátoru s operačním zesilovačem (viz kapitola Analogové zpracování signálu). Vytvoříme-li z takového integrátoru generátor, je jeho kmitočet úměrný C^-1. Změříme-li proto kmitočet takového generátoru s neznámým kondenzátorem, můžeme po jednoduché kalibraci (změříme kmitočet se známým kondenzátorem a z toho zjistíme konstantu úměrnosti) rychle měřit kapacity tím, že jsme převedli měření kapacity na měření kmitočtu.

Kmitočet měříme pomocí čitače impulsů jako počet period za definovanou dobu, obvykle dekadický násobek nebo zlomek jedné sekundy. O čitačích impulsů se můžete dočíst v kapitole Základy číslicových obvodů. Jakékoli jiné metody měření jsou v současné době prakticky již muzeální vzhledem k tomu, že popsanou metodou je nyní možné měřit kmitočty od zlomku Hz do desítek GHz. V kabinetech se můžete setkat s absorpčním vlnoměrem, jazýčkovým kmitočtoměrem a pokud budete mít k dispozici osciloskop, můžete předvést i Lissajousovy obrazce.

Osciloskop