Krystalová struktura látek se popisuje pomocí tzv. přímé krystalové mříže a báze spojené s každým mřížovým bodem. Krystalové roviny a směry se popisují Millerovými indexy. S každou přímou krystalovou mříží je svázána reciproká mříž vztahy

kde představují translační vektory krystalové mříže a představují vektory reciproké mříže.

            Millerovy indexy:

Slouží pro popis rovin v krystalech. Postup, jak je získat, je následující:

1.             Najdeme body, v nichž daná rovina protíná souřadné osy v jednotkách základních mřížkových parametrů

2.             Vezmeme převrácené hodnoty těchto čísel a převedeme je na nejmenší úměrná celá čísla.

Potom platí, že vzdálenost dvou krystalových rovin d charakterizovaných indexy (h,k,l) je rovna 2p/b, kde b je velikost vektoru reciproké mřížky , kde platí že

g₁: g₂: g₃ = h:k:l

Geometrická teorie difrakce

Elektronům lze podle kvantové mechaniky přiřadit vlnu, která je charakterizovaná vlnovým vektorem 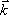. Tento vektor má směr postupu vlny a velikost , kde l je vlnová délka, která závisí nepřímo úměrně na odmocnině z energie elektronů. Energie elektronů je pak dána urychlujícím napětím elektronové trysky. Při dopadu monoenergetického elektronového svazku na terč dochází k interakci tohoto vlnění s atomy mříže a k ohybovým a difrakčním jevům. Vlny rozptýlené na jednotlivých atomech spolu totiž interferují a periodické uspořádání atomů v krystalech vede k dráhovým rozdílům mezi vlnami a tím k zesílení nebo k zeslabení těchto vln. Ohyb elektronů je vhodný ke zkoumání struktury podobně jako rentgenové záření. Rozdíly mezi RTG a elektrony jsou dány rozdílnou vlnovou délkou a vzájemným působením s atomy vzorku. Pokud porovnáme účinné průřezy elektronů a RTG záření pro pružný rozptyl, zjistíme, že účinný průřez pro elektrony je o šest až osm řádů větší než účinný průřez pro rentgenové záření. Potom stačí podstatně menší množství materiálu, aby byly získány dostatečné rozptylové intenzity. Elektrony jsou ale více rozptylovány nepružně a absorbovány, takže mohou pronikat jen do podstatně menších hloubek.

Geometrická teorie difrakce vychází z předpokladu, že na všech rozptylových centrech v terči je rozptylována primární vlna s vlnovou délkou l. Vícenásobný rozptyl je zanedbáván. Při řešení se předpokládá, že rozptylová centra jsou zdrojem vlnění, která spolu interferují a jako výsledek získáme směry ohybových maxim.

Krystalové roviny a směry se popisují Millerovými indexy.

Podmínku difrakčního maxima lze vyjádřit jako ,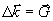

kde 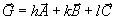 je vektor reciproké mříže, h,k,l jsou Millerovy indexy a  je rozdíl dopadajícího a odraženého vlnového vektoru. Podle předpokladu tedy bereme v úvahu pouze elasticky rozptýlené elektrony, platí tedy, že se mění pouze směr a nikoli velikost vlnového vektoru. Z těchto skutečností plyne tzv. Ewaldova konstrukce, kterou vystihuje obrázek:

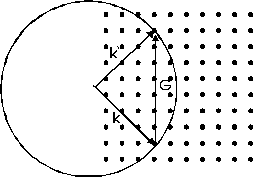
Obrázek 1: Ewaldova konstrukce v případě objemové difrakce

Primární paprsek elektronů je reprezentován vektorem 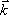, sekundární odražený paprsek vektorem 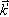. Směry difrakčních maxim potom určují průsečíky Ewaldovy sféry o poloměru 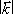 s body reciproké mříže. Ze zobrazených difrakčních bodů tedy dostáváme  zobrazení reciproké mříže. Z teorie difrakce plyne, že reciproká mříž atomárně rovného povrchu, který má nekonečné rozměry je složena z linií kolmých k povrchu.

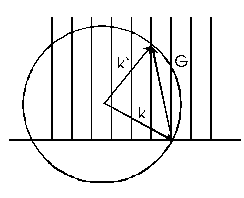
Obrázek 2: Ewaldova konstrukce v případě povrchové difrakce

Copyright (c) 2004 KEVF. All rights reserved.

kevf(at)email.cz