Rovinný magnetron (planotron)

Doposud jsme elektromagnetické pole v magnetronové dutině považovali za kmity. Fázové posunutí mezi sousedními štěrbinami muselo vyhovovat podmínce , která plynula z toho, že struktura obvodových rezonátorů - neboli periodická struktura - byla kruhově uzavřená. Dospějeme však ke stejnému výsledku, budeme-li elektromagnetické pole v magnetronové dutině považovat za elektromagnetickou vlnu, která postupuje dokola (rotuje). Geometrický úhel mezi středy sousedních štěrbin je  . Vlna postoupí od jedné štěrbiny k následující za čas , potom úhlová rychlost rotující vlny je w.

Fázový rozdíl mezi sousedními štěrbinami je j.

Z hlediska pozorovatele, který se pohybuje s postupující vlnou musí tedy platit

tj.

odkud

Číslo  je celé číslo, takže . Ke každému  patří řada vln, které jsou zpomalené, jejich úhlová rychlost je nižší než frekvence w příslušného kmitu. Největší rychlostí se pohybuje základní vlna pro m = 0. Pro modus p  je .

Co jsme chtěli tímto rozborem naznačit?

Rezonanční struktura magnetronové dutiny pracuje jako zpomalovací struktura. Zpomaluje elektromagnetické vlny, čímž je vlastně umožněna jejich silná interakce s elektrony. Je patrně poněkud „nepřirozené“ kmity v uzavřené dutině považovat za rotující vlnu (vlny). Můžeme si však představit, že válcový magnetron rozřízneme a narovnáme. Dostaneme tak rovinný magnetron (obr. 7.2.1), kde již elektromagnetická vlna nerotuje, ale postupuje vpřed zpomalenou rychlostí. Tento rovinný magnetron je přístupnější analytickým metodám výpočtu trajektorií, tvaru zakázaných oblastí atd. Jeho teorií se zabýval P. Kapica, který též provedl experimenty s laboratorně vyrobeným rovinným magnetronem, který nazval planotron.

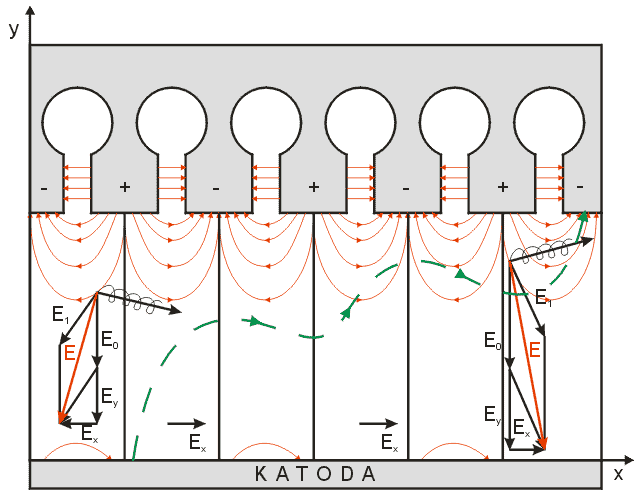
Obr. 7.2.1  Rovinný magnetron

Rovinný magnetron byl použit též Slaterem pro odhad účinnosti. Bez přítomnosti vysokofrekvenčního pole se v rovinném magnetronu pohybují elektrony ve zkřížených homogenních polích po známých trajektoriích - cykloidách. Maximální kinetická energie je při cykloidálním pohybu elektronu je rovna ( E, B homogenní zkřížená pole). Kritické hodnoty E_K, B_K odpovídají situaci, kdy výška cykloidy se rovná 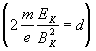 vzdálenosti mezi katodou a anodou, přičemž U_a = E.d. Slater uvažoval při odhadu účinnosti takto:

Všechna energie, kterou nabyl elektron ze stejnosměrného pole se přemění ve vysokofrekvenční energii, až na tu část, která disipuje při dopadu elektronu na anodu. Disipovaná energie odpovídá nějaké kinetické energii elektronu u anody. Za ní považuje Slater maximální kinetickou energii cykloidálního pohybu. Je to tedy určité vystředování, neboť některé elektrony dopadají s menší, jiné s větší energií na anodu, protože ztratily nebo získaly energii z vysokofrekvenčního. Obecně je elektronická účinnost dána

Použitím rovinného modelu a dosazením za  dostaneme jednoduchý vztah

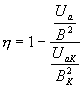
který již neobsahuje geometrii magnetronu a dá se aplikovat i na válcový magnetron. Při kritických hodnotách klesá účinnost k nule - magnetron přestává generovat. Uvedený vztah nezapočítává ztráty vzniklé odebíráním vysokofrekvenční energie elektrony, které se vracejí na katodu a zahřívají ji. Ze zkušenosti je známo, že tyto ztráty obnášejí několik procent přivedeného stejnosměrného výkonu.

Dosahovaný užitečný výkon magnetronových generátorů obnáší řádově 10 - 100 kW. Magnetrony však často pracují v pulzním režimu. Délka pulzu ~ 1 ms, délka mezery ~ 1 ms.  To zvýší okamžitý výkon v pulzu do řádu až 100 MW.

Na obr. 7.2.2 jsou znázorněny magnetronové dutiny dvou různých typů s odvodem energie pomocí smyčky a štěrbiny (v druhé dutině není zakreslena katoda).

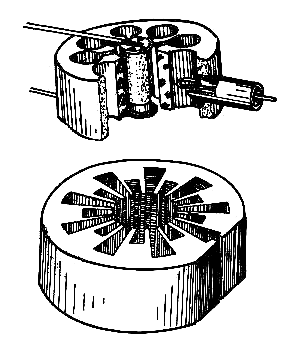
Obr. 7.2.2  Magnetronové dutiny

<<< předchozí | hlavní stránka | další >>>