V předchozích článcích jsme se seznámili s přechody jednosložkové soustavy z jednoho skupenství do druhého. Při těchto přechodech se výrazně mění téměř všechny fyzikální vlastnosti látky. Za určitých podmínek se mohou změnit prakticky skokem některé fyzikální vlastnosti i u látek, které jsou v jednom skupenství. Pro popis těchto jevů se zavádí pojem fáze a fázového přechodu. Říkáme, že soustavu tvoří jediná fáze, jestliže všechny části uvažované soustavy mají stejné fyzikální a chemické vlastnosti. Taková soustava se pak nazývá homogenní soustava na rozdíl od heterogenní soustavy, která je složena z více fází.
Termín fáze má obecnější význam než skupenství. Různá skupenství látky jsou vždy různými fázemi. Rozdílné fáze mohou však existovat i ve stejném skupenství. Příkladem může být grafit a diamant. Oba materiály mají stejné chemické složení (jedná se o uhlík) a oba jsou v pevném skupenství. Liší se však výrazně svými fyzikálními vlastnostmi danými různým prostorovým uspořádáním atomů uhlíku. Grafit, krystalizující v hexagonální soustavě, je neprůhledný a měkký. Diamant má kubickou strukturu a je nejtvrdším minerálem vůbec.
Pro jakýkoliv fázový přechod zůstává splněna podmínka (8.6), ve které G1 a G2 má význam volné entalpie prvé a druhé fáze. Důvodem je opět okolnost, že obě fáze mohou v rovnováze koexistovat pouze při stejném tlaku a teplotě. Podmínka (8.6) vyjadřuje, že při stejné teplotě a tlaku, ovšem i při hmotnosti látky, jsou si volné entalpie obou fází rovny, tj. platí
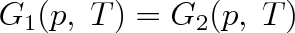 |
(8.24) |
Volná entalpie soustavy jako celku se při přeměně látky z jedné fáze do druhé (při fázovém přechodu) nezmění.
Při různých fázových přechodech však nemusí zůstávat konstantní derivace volné entalpie. Ze vztahu (8.4) plyne, že
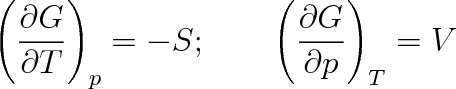 |
(8.25) |
Jsou-li obě tyto derivace stejné pro obě fáze, mluvíme o fázovém přechodu II. druhu, jestliže se liší, jedná se o fázový přechod I. druhu. Toto jej kritérium pro dělení fázových přechodů podle Ehrenfesta. Pro oba druhy fázových přechodů je schématicky v obr. 8-3 zakreslena závislost objemu na teplotě. Teplotu fázového
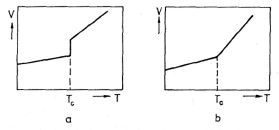 Obr. 8-3
Obr. 8-3
přechodu určuje pro fázový přechod I. druhu skok v závislosti V = V(T) nebo S = S(T). Pro fázový přechod II. druhu odpovídá teplota fázového přechodu teplotě zlomu na této závislosti.
Je zřejmé, že podle této klasifikace jsou skupenské přeměny fázovými přechody I. druhu. Při nich se mění objem, entropie a řada dalších veličin skokem. Tyto fázové přechody popisuje Clausiova-Clapeyronova rovnice (8.10).
Při fázových přechodech II. druhu dochází zpravidla ke změně struktury látky najednou v celé soustavě. Nejběžnější jsou tyto fázové přechody v krystalických pevných látkách. Dosažení teploty fázového přechodu II. druhu je příčinou změny v symetrii prostorového uspořádání atomů. Protože přechod se uskutečňuje současně v celém prostoru zaujmutém soustavou, nemohou být spolu v rovnováze dvě fáze a přechod není doprovázen uvolněním nebo dodáním skupenského tepla. Protože se nemění skokem ani měrný objem, nezmění se ani vnitřní energie. Skokem se však změní molární tepelná kapacita, která je úměrná derivaci molární vnitřní energie podle teploty, CmV = dUm/dT. Nespojitě se změní i součinitel teplotní objemové roztažnosti,
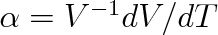 .
.
Podrobněji se věnujme problematice fázového přechodu II. druhu v krystalických pevných látkách. Pokud tento fázový přechod probíhá za konstantního tlaku, jedná se o děj izobarický a přibližně i izochorický, protože se při něm nemění měrný objem. Pak ovšem jsou členy Vdp a pdV ve výrazu (8.3) pro změnu volné entalpie rovny nule. Diferenciál volné entalpie dG bude za těchto
podmínek roven diferenciálu volné energie, která je definována vztahem (viz 4.20)
 |
(8.26) |
ve kterém ř/je vnitřní energie, T termodynamická teplota a S entropie soustavy. Úplný diferenciál volné energie dFje roven
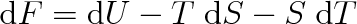 |
(8.27) |
Protože molární tepelné kapacity Cmp a CmV jsou si v pevných látkách téměř rovny (viz str. 52), můžeme změnu molární vnitřní energie a entropie v pevných látkách vyjádřit přibližně vztahy
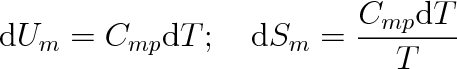 |
(8.28) |
Po dosazení do (8.27) dostaneme jednoduchý výraz pro změnu molární volné energie
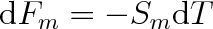 |
(8.29) |
Integrováním od 0 K do teploty T získáme pro molární volnou energii výraz
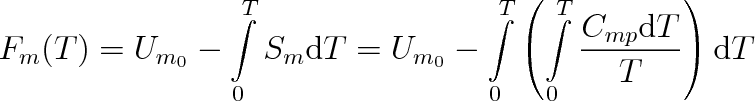 |
(8.30) |
Integrační konstanta Um0 je rovna molární volné energii při teplotě 0 K. Použili jsme pro její označení stejný symbol jako pro vnitřní energii. Můžeme to udělat, protože podle vztahu (8.26) je při 0 K volná energie rovna vnitřní energii.
Protože integrandy ve výrazu (8.30) jsou kladné, klesá molární volná energie monotónně s rostoucí teplotou. Pokles je tím rychlejší, čím větší je molární tepelná kapacita soustavy. Uvažujeme-li krystalickou látku, ve které by mohly být atomy prostorově rozmístěny dvěma různými způsoby, mohla by tato látka existovat ve dvou strukturních modifikacích. Vazebné síly atomů budou pravděpodobně pro každou modifikaci jiné, rozdílné proto budou i molární vnitřní energie Um0. Nechť je například molární vnitřní energie Um0 modifikace a (fáze a) menší než u fáze
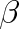 ,
,
 . Znamená to, že vazebné síly ve fázi a jsou větší, než ve fázi
. Znamená to, že vazebné síly ve fázi a jsou větší, než ve fázi
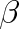 . Velikost vazebních sil má vliv na hodnotu molární tepelné kapacity; čím jsou větší, tím menší je molární tepelná kapacita Cmp . Fáze
. Velikost vazebních sil má vliv na hodnotu molární tepelné kapacity; čím jsou větší, tím menší je molární tepelná kapacita Cmp . Fáze
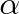 bude mít menší molární tepelnou kapacitu a molární volná energie
bude mít menší molární tepelnou kapacitu a molární volná energie
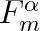 bude klesat s rostoucí teplotou pomaleji, než ve fázi
bude klesat s rostoucí teplotou pomaleji, než ve fázi
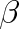 . Schématicky je závislost molární volné energie na teplotě zakreslena na obr. 8-4. Stabilní je vždy ta modifikace, které přísluší nižší hodnota volné energie. Při nízkých teplotách bude proto látka
. Schématicky je závislost molární volné energie na teplotě zakreslena na obr. 8-4. Stabilní je vždy ta modifikace, které přísluší nižší hodnota volné energie. Při nízkých teplotách bude proto látka
existovat ve fázi a. V bodě, kde se obě křivky protínají, dojde k přechodu do fáze
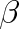 . Popisovaný přechod je fázovým přechodem II. druhu. Mluví se o něm též jako o polymorfní změně. Aby k tomuto přechodu došlo, musí být ovšem teplota Tc nižší než teplota tání Tt (Tc < Tt).
. Popisovaný přechod je fázovým přechodem II. druhu. Mluví se o něm též jako o polymorfní změně. Aby k tomuto přechodu došlo, musí být ovšem teplota Tc nižší než teplota tání Tt (Tc < Tt).
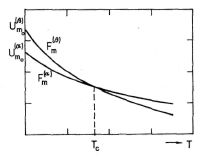 Obr. 8-4
Obr. 8-4
Na látku nemusí působit pouze mechanické silové pole, realizované např. tlakovou silou. Látka může být i pod vlivem elektrického nebo magnetického pole. Volná energie pak závisí též na veličinách, které charakterizují silové působení těchto polí, na intenzitě E elektrického nebo indukci B magnetického pole.
Atomy železa, niklu a řady dalších látek mají nenulový magnetický dipólový moment i v nulovém magnetickém poli. Tyto látky se nazývají paramagnetické. Při vysokých teplotách brání tepelný pohyb paralelnímu uspořádání dipólových momentů, takže bez magnetického pole má soustava nulový magnetický moment. Sníží-li se však teplota, dojde u některých paramagnetických látek k přechodu do feromagnetického stavu. Teplota, při níž se tento přechod uskuteční, se nazývá Curieova teplota Tc. Ve feromagnetickém stavu existují makroskopické oblasti (domény), v nichž jsou dipólové momenty uspořádány paralelně. V mag-
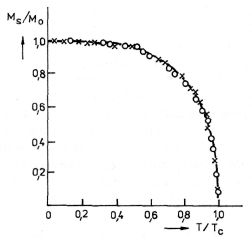 Obr. 8-5
Obr. 8-5
netickém poli se pak orientují celé domény do směru vektoru B magnetické indukce. Tato orientace zůstane částečně zachována i po zrušení magnetického pole. Látka zůstane zmagnetována.
Přechod z paramagnetického do feromagnetického stavuje fázovým přechodem II. druhu, neboť se výrazně mění fyzikální vlastnosti látky. Závislost poměrné velikosti dipólového momentu jednotky objemu (poměrné magnetizace Ms/M0) železa a niklu na poměru teploty T a teploty fázového přechodu Tc je zakreslena na obr. 8-5. Veličina M0 znamená hodnotu magnetizace při T -» 0 K. Při teplotě fázového přechodu Tc se mění magnetická polarizace spojitě. Protože magnetická polarizace je určena první derivací volné energie F, mění se spojitě i
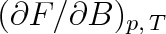 a podle Ehrenfestova třídění fázových přechodů se jedná o přechod II. druhu. V tabulce 8-7 uvádíme teploty Tc několika feromagnetických látek.
a podle Ehrenfestova třídění fázových přechodů se jedná o přechod II. druhu. V tabulce 8-7 uvádíme teploty Tc několika feromagnetických látek.
Tabulka 8-7 Curieovy teploty feromagnetických látek
|
Látka |
Curieova teplota (K) |
Látka |
Curieova teplota (K) |
|
Co |
1 394 |
MnBi |
630 |
|
Fe |
1 043 |
Cu2MnAl |
600 |
|
Ni |
631 |
Cu2MnSn |
533 |
|
Gd |
289 |
Au2MriAl |
258 |
|
Tb |
229 |
UH3 |
180 |
|
Dy |
105 |
||
|
Ho |
20 |
Domény se mohou vytvářet i v pevných látkách, ve kterých molekuly nebo skupiny iontů mají permanentní elektrický dipólový moment. Tyto látky se nazývají feroelektrické látky. K fázovému přechodu II. druhu dochází při Curie-ově teplotě Tc. Se snižováním teploty se mění stav s neuspořádanými elektrickými dipólovými momenty ve stav uspořádaný. Elektrická polarizace se při přechodu do feroelektrického stavu může měnit buď spojitě, pak se jedná opět o fázový přechod II. druhu, nebo skokem, což znamená, že se jedná o fázový přechod I. druhu. Jednou z nejzajímavějších feroelektrických látek je titaničitan barnatý BaTiO3, který má tak zvanou perovskitovou strukturu, viz obr. 8-6. V rozích krychle jsou ionty Ba2+, uprostřed Ti4+ a ionty O2- jsou ve středu stěn. Při
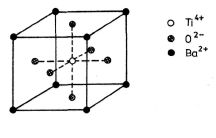 Obr. 8-6
Obr. 8-6
teplotách pod Curieovou teplotu (Tc = 293 K) se poněkud posunou ionty Ba2+ a Ti2+ vůči kyslíku, čímž vznikne dipólový moment. Další snižování teploty pak vede ještě dvakrát ke změně struktury. Závislost velikosti spontánní polarizace P na teplotě je pro BaTiO3 zakreslena na obr. 8-7.
 Obr. 8-7
Obr. 8-7
O fázovém přechodu II. druhu mluvíme i v případě přechodu kovů z normálního do supravodivého stavu. Prvý tento jev pozoroval H. Kammerling-Onnes v roce 1911 u rtuti. Fázový přechod probíhá u rtuti při teplotě 4,16 K. Později byl nalezen u celé řady čistých materiálů a slitin. Bylo prokázáno, že se jedná o stav elektrického odporu a nikoli pouze o stav s malým elektrickým odporem. V souvislosti s teplotní stupnicí EPT 87 jsme pro několik látek uvedli teploty supravodivého přechodu v tabulce 7-6. Další hodnoty jsou zaznamenány v tabulce 8-8. Supravodivé materiály se již využívají v technické praxi, především v supravodivých solenoidech.
Tabulka 8-8 Teploty supravodivých přechodů
|
Materiál |
Nb3Al0,8Ge0,2 |
Nb3Sn |
Nb |
V |
Sb |
InSb |
Mo |
|
Tc[K] |
20,05 |
18,05 |
9,2 |
5,3 |
2,6 |
1,9 |
0,92 |
V roce 1986 byl švýcarskými fyziky K. A. Mullerem a J. G. Bednorzem objeven přechod do supravodivého stavu u oxidů keramické povahy. Tento objev byl převratný, neboť naznačil, že supravodivost lze hledat i u látek, které se považovaly za izolanty.
Během roku 1987 americký fyzik čínského původu C. W. Chu zjistil supravodivost u multifá-zového materiálu, který má přibližné chemické složení YBa2Cu307 (ybacuo) při teplotě okolo 90 K. Zde se již mluví o vysokoteplotní supravodivosti, neboť supravodivosti lze dosáhnout při chlazení kapalným dusíkem (teplota varu 77 K). Chlazení dusíkem je asi tisíckrát lacinější než chlazení heliem. Tím se nesmírně zvýšily naděje na široké technické využití supravodivosti.
Výzkum v této oblasti je velmi intenzívní. Je reálná naděje, že se podaří připravit materiály, které budou stabilně supravodivé i při teplotách vyšších, než je pokojová teplota. Očekává se, že objev vysokoteplotní supravodivosti bude příčinou převratných změn v technických oblastech, ve kterých se využívají silná magnetická pole (pohonné systémy, diagnostické přístroje, magnetické separátory, urychlovače částic, termojaderná syntéza) a kde je výhodný bezeztrátový (energetika) a rychlý (mikroelektronika) přenos elektrické energie.
Z fyzikálního hlediska je mimořádně zajímavý fázový přechod kapalného helia
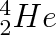 do supratekutého stavu. Tento přechod se uskutečňuje za normálního tlaku při teplotě 2,17 K. Graf teplotní závislosti měrné tepelné kapacity je znázorněn na obr. 8-8. V supratekutém stavu poklesne viskozita helia na nulu
do supratekutého stavu. Tento přechod se uskutečňuje za normálního tlaku při teplotě 2,17 K. Graf teplotní závislosti měrné tepelné kapacity je znázorněn na obr. 8-8. V supratekutém stavu poklesne viskozita helia na nulu
 Obr. 8-8
Obr. 8-8
a kapalina proudí i bez tlakového spádu velmi úzkými kanálky. Někteří autoři považují tento přechod za přechod II. druhu, většinou je však považován za zvláštní druh fázového přechodu. Nazývá se
 - přechod podle anomálního tvaru teplotní závislosti měrné tepelné kapacity, připomínající řecké písmeno
- přechod podle anomálního tvaru teplotní závislosti měrné tepelné kapacity, připomínající řecké písmeno
 . Supratekutá složka se označuje jako HeII na rozdíl od normálního tekutého helia HeI.
. Supratekutá složka se označuje jako HeII na rozdíl od normálního tekutého helia HeI.
Poukázali jsme na mnohotvárnost problematiky fázových přechodů. I když jsme uvedli řadu příkladů, přesto jejich výčet není úplný. Existují třeba fázové přechody v kapalných krystalech, difúzní fázové přechody atd.