8.4 Tlak syté páry

Vpravíme-li do uzavřené prázdné nádoby kapalinu, přemění se část kapaliny v páru, která vyplní prostor nad kapalinou. Měříme-li tlak této páry, zjistíme, že nezávisí na vnitřních rozměrech nádoby a hmotnosti kapaliny v nádobě. Měření při různých teplotách ukáže, že tlak silně závisí na teplotě. Tlak naměřený v daném uspořádání nazýváme tlakem syté páry.

Tabulka 8-5 Teploty a tlaky syté páry různých látek

Látka			Tlak	sytých par	P_S (Pa)
Teplota r(K)
Teplota r(K)	1,33 . 10^-8	1,33 . 10^-6	1,33 . 10^-4	1,33 . 10^-2	1,33	1,33 . 10²	1,33 . 10⁴
helium						1,268	2,85
dusík		23,7	27	31,4	37,5	47,0	63,4
kyslík		29,2	31,9	36,7	43,3	54,1	74,3
oxid uhličitý		76,1	85,7	98,1	114,5	137,5	173
voda		144,5	162	185	215	256	324
rtuť	184	205	231	267	319	398	527
hliník	824	917	1 039	1 200	1 421	1 745	2 269
cín	855	961	1 096	1 275	1 521	1 890	2 518
železo	1 019	1 131	1 271	1 453	1 698	2 063	2 633
wolfram	2 154	2 383	2 667	3 029	3 502	4 147	5 083

Závislost hustoty N_v molekul na jejich energii U dává Boltzmannův vztah, podle kterého

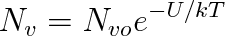(8.15)

Zde znamená N_vo hustotu molekul při U = 0, k je Boltzmannova konstanta a T termodynamická teplota.

Tento vztah můžeme použít k výpočtu teplotní závislosti tlaku syté páry. Energie molekul v plynném skupenství je vyšší než v kapalině. Pro látkové

množství 1 mol je molární skupenské teplo výparné L_m. Jedna molekula v plynu má proto v průměru o L_m/N_A vyšší energii než v kapalině, je-li N_A Avogadrova konstanta. Porovnáme-li změnu hustoty molekul vůči kapalině (U = 0; N_vo = N_k), bude v plynu N_v = N_p a U = L_m/N_A. Po dosazení do (8.15) dostaneme, že

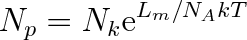(8.16)

Hustota molekul plynu souvisí s tlakem vztahem p = N kT . Uvážíme-li ještě, že kN_A je rovno molární plynové konstantě R, dostaneme pro tlak plynu nad kapalinou

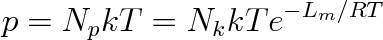Po logaritmování dostaneme výraz

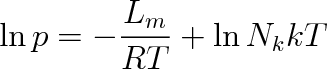(8.17)

Druhý člen na pravé straně této rovnice se mění s teplotou pomaleji než první, je možné tuto závislost zanedbat a pokládat jej za konstantu.

Na závěr tohoto článku se ještě krátce zmíníme o vodní páře v zemské atmosféře. Hmotnost vodní páry se mění v denní i roční době a závisí podstatně i na místě na Zemi. Větší hmotnost vodní páry je v ovzduší zpravidla odpoledne než

Tabulka 8-6 Teploty normálního bodu varu a teploty kritické

Kapalina	Teplota kritická	Teplota varu	T_v/T_k
Kapalina	T_k (K)	T_v(K)	T_v/T_k
voda H₂0	647	373	0,58
benzen C₆H₆	562	353	9,63
etylalkohol C₂H₅OH	516	351	0,68
oxid siřičitý S0₂	431	263	0,61
sirovodík H₂S	373	213	0,57
oxid uhličitý C0₂	304	195	0,64
kyslík 0₂	155	90	0,58
dusík N₂	126	77	0,61
vodík H₂	33	20	0,61

ráno, v létě než v zimě, na pobřeží než ve vnitrozemí. Na hmotnosti vodní páry závisí četnost dešťových srážek i fyziologický pocit člověka. Lépe se snáší vyšší teplota při malé hmotnosti vodní páry. Zavedeme nyní některé veličiny, kterými se charakterizují vlastnosti vodní páry v ovzduší.

Absolutní vlhkost vzduchu je poměr hmotnosti m vodní páry ve vzduchu o objemu V a tohoto objemu, neboli

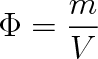(8.21)

Při dané teplotě nemůže být absolutní vlhkost vzduchu libovolně velká. Může vzrůstat jen do maximální hodnoty , při jejímž dosažení začne vodní pára kondenzovat. Stane se tak, je-li parciální tlak vodní páry roven tlaku syté vodní páry p_s. Absolutní vlhkost a parciální tlak vodní páry jsou veličiny přibližně si úměrné, bude proto teplotní závislost maximální možné absolutní vlhkosti prakticky stejná jako teplotní závislost tlaku syté vodní páry.

Lepší informaci o tom, jak je ovzduší vlhké, poskytuje veličina relativní vlhkost . Definujeme ji vztahem

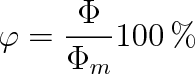(8.22)

Protože absolutní vlhkost je úměrná tlaku vodní páry, můžeme také psát

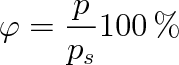(8.23)

znamená-li p parciální tlak vodní páry a p_s tlak syté páry.

Vlhkost ovzduší je možno charakterizovat též rosným bodem. Je to stav popsaný teplotou T_r, na kterou by bylo třeba ochladit vzduch, aby tlak syté vodní páry v rosném bodě p_s (T_T) byl roven parciálnímu tlaku vodní páry při teplotě T; (p_s(T_r) = p(T)).

Zobrazit doplňující text

[13] Brož J., Roskovec V., Valouch M.: Fyzikální a matematické tabulky, SNTL, Praha 1980