V předchozím článku jsme se seznámili se stavovým diagramem jednosložkové soustavy a vysvětlili si za jakých podmínek dojde ke změně skupenství. V tomto článku odvodíme matematický vztah, který vyjadřuje, jak se změní tlak, změní-me-li teplotu, při níž se uskutečňuje změna skupenství.
Vyjdeme z volné entalpie, která je definována vztahem (viz čl. 4.7)
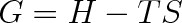 |
(8.1) |
v němž T je termodynamická teplota, S entropie a H entalpie, přičemž
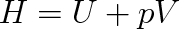 |
(8.2) |
Úplný diferenciál volné entalpie bude roven
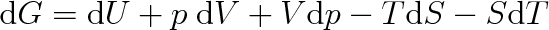 |
(8.3) |
Protože podle 1. a II. termodynamického zákona (viz články 3.2 a 4.3) je
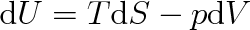 |
bude platit (viz též vztah (4.24))
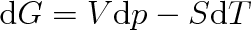 |
(8.4) |
Jsou-li obě skupenství látky v mechanické a tepelné rovnováze, pak mají stejnou teplotu a stejný tlak. Proto je dp = 0 i dT = 0, a platí
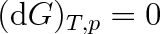 |
(8.5) |
Změníme-li v soustavě buď tlak, nebo teplotu, změní se i volná entalpie. Pro skupenství 1 bude platit
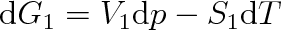 |
a obdobně pro skupenství 2 vztah
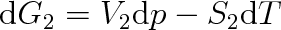 |
Aby i po vyvolané změně tlaku nebo teploty byla soustava v rovnováze platí
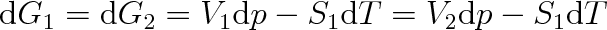 |
(8.7) |
Změny veličin p a T jsou v tomto případě nenulové (dp
 0, dT
0, dT
 0), takže můžeme psát
0), takže můžeme psát
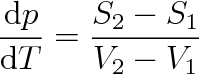 |
(8.8) |
Změnu entropie S2 - S1 můžeme vyjádřit pomocí skupenského tepla L, které jsme museli soustavě dodat nebo odebrat. Protože změna skupenství probíhá za konstantní teploty, můžeme psát, že platí
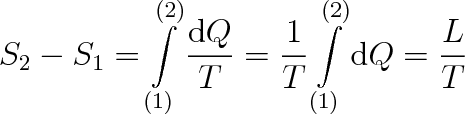 |
(8.9) |
Po dosazení ze vztahu (8.9) do vztahu (8.8) dostaneme rovnici
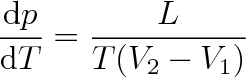 |
(8.10) |
která se nazývá Clausiova-Clapeyronova rovnice. Uvažuje-li se skupenská přeměna v soustavě o látkovém množství 1 mol, znamená v této rovnici L molární skupenské teplo (L = Lm) a V1, V2 jsou molární objemy látky (V1 = Vm1, V2 = Vm2).
Při odvození rovnice (8.10) jsme nespecifikovali, o jakou změnu skupenství se jedná. Měla by proto platit jak pro přechod pevná látka - kapalina, tak i kapalina - plyn a samozřejmě i pro přechody opačné. Při kondenzaci je vždy objem kapaliny menší než objemu plynu (V2 - V1) < 0, zároveň je i skupenské teplo dodané soustavě záporné, L < 0, neboť při kompresi musíme teplo soustavě odebírat, abychom udrželi konstantní teplotu. Znamená to, že při kondenzaci je vždy pravá strana rovnice (8.10) kladná. Proto zvýšíme-li teplotu soustavy (dT > 0), zvýší se i tlak syté páry (dp > 0).