Hledání univerzálně platné stavové rovnice bylo, především na konci minulého století, věnováno mnoho času a úsilí. Toto hledání však vedlo jen k dílčím úspěchům. Všechny nalezené stavové rovnice, kterých je hodně, mají omezenou platnost. Konečně vyřešení problému nepředstavuje ani využití teorému korespondujících stavů. Zbývá ještě jedna cesta, vyjádřit stavové chování rozvojem s nekonečným počtem členů.
Nekonečnou řadou se zpravidla vyjadřuje kompresibilitní faktor. Nezávisle proměnnou může být kterákoli stavová veličina, koeficienty u členů řady jsou závislé na jedné z dalších stavových veličin. Například tzv. tlakový rozvoj je vyjádřen řadou s mocninami tlaku, koeficienty jsou závislé na teplotě.
Nejvýznamnější je však rozvoj, který navrhl r. 1901 H. Kamerlingh-ONNES (Nizozemec, 1853-1926). Představuje jej řada, v níž je nezávisle proměnnou reciproký molární objem 1/Km:
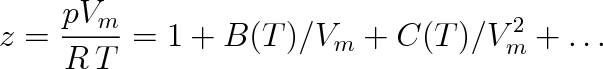 |
(7.19) |
Tento vztah se nazývá viriálním rozvojem. Koeficienty u mocnin 1/Vm jsou obecně závislé na teplotě a nazývají se druhý, třetí atd. viriální koeficient. První viriální koeficient ve vztahu (7.19) je roven jedné. Je pochopitelné, že čím větší počet vhodně volených viriálních koeficientů zahrneme do výpočtu, tím přesněji popíšeme chování reálného plynu. Teorericky můžeme popsat stavové chování plynu viriálním rozvojem libovolně přesně. Pro praktické užití však postačuje rozvoj s druhým, případně i třetím viriálním koeficientem.
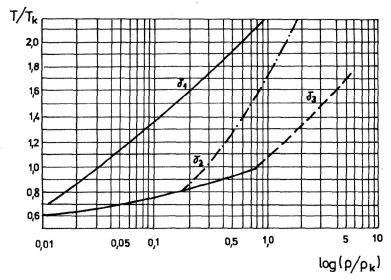 Obr. 7-6
Obr. 7-6
Přesnost viriální rovnice s různým počtem viriálních koeficientů lze pro běžný obor tlaků a teplot odečíst z obr. 7-6. Na tomto obrázku jsou vyneseny tři křivky konstantní relativní chyby
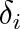 = 1 %. Index i určuje, kolik členů řady (7.19) je nutno při výpočtu použít. V oblasti nad křivkami je přesnost stanovení kompresibilitního faktoru lepší než 1 %, pod nimi horší. Nad křivkou
= 1 %. Index i určuje, kolik členů řady (7.19) je nutno při výpočtu použít. V oblasti nad křivkami je přesnost stanovení kompresibilitního faktoru lepší než 1 %, pod nimi horší. Nad křivkou
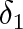 můžeme používat stavové rovnice ideálního plynu s přesností ± 1 %.
můžeme používat stavové rovnice ideálního plynu s přesností ± 1 %.
Viriálním rozvojem můžeme vystihnout nejen skutečné stavové chování plynů, ale i průběhy modelované stavovými rovnicemi. Upravíme-li stavovou rovnici tak, aby na levé straně rovnice vystupoval pouze kompresibilitní faktor, budou viriální koeficienty rovny koeficientům u příslušných mocnin 1/Vm na pravé straně upravené stavové rovnice. Pro stavovou rovnici ideálního plynu je nenulový pouze první viriální koeficient. Jednoduchým výpočtem, při kterém provedeme rozvoj výrazu (1 - b/Vm)-1 podle b/Vm, dostaneme z van der Waalsovy rovnice následující výrazy pro druhý a třetí viriální koeficient:
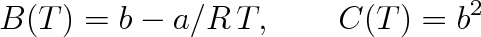 |
(7.20) |
Nenulové jsou i další viriální koeficienty, a sice rovné vyšším mocninám koeficientu b.
Z toho, co jsme zatím napsali o viriální rovnici, neplyne její skutečný význam. Mohli bychom soudit, že se jedná pouze o stavovou rovnici s volitelným počtem teplotně závislých koeficientů. Již dříve, než byl podán exaktní důkaz, se usuzovalo, že viriální koeficienty charakterizují vzájemné silové působení dvojic, trojic atd. molekul. Víme, že v silně zředěném plynu je možno zanedbat i silovou interakci dvojic molekul. Vystačíme pak jen s prvním viriálním koeficientem a stavové chování plynu popisuje stavová rovnice ideálního plynu. Viriální rozvoj se dvěmi viriálními koeficienty by měl správně popisovat stavové chování plynu v oboru hustot, ve kterém je sice nutno uvažovat interakci dvojic molekul, ale současná interakce tří molekul je nepravděpodobná. Obdobně by tomu mělo být pro viriální rozvoj s větším počtem členů.
Odvození výrazů pro vyšší viriální koeficienty je mimořádně obtížné a nelze je uvést v rámci této knihy. Musíme se spokojit s konstatováním, že původně intuitivní představa byla exaktně potvrzena. Uvedeme zde pouze výraz pro druhý viriální koeficient látek s prostorově i nábojově symetrickými molekulami, který má tvar (viz např. [11])
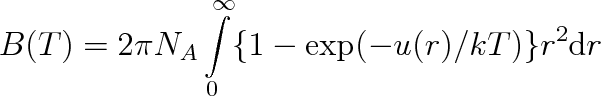 |
(7.21) |
[11] Odvození tohoto výrazu nalezne čtenář například v Dodatku 2 knihy Novák J. P., Malijevský A., Šobr J., Matouš J.: Plyny a plynné směsi, Academia, Praha 1972. Tato kniha se podrobně zabývá problematikou reálných plynů.
Zde znamená r vzdálenost molekul, NA Avogadrovu konstantu, k Boltzmanovu konstantu a T termodynamickou teplotu.
Pro symetrické molekuly je potenciální energie u(r) vzájemného silového působení dvou molekul dána výrazem typu (7.16). Pro nesymetrické molekuly závisí tato energie nejen na vzdálenosti, ale i na jejich vzájemné orientaci. Výraz (7.21) pak bude složitější. Postupně se stávají složitější i výrazy pro vyšší viriální koeficienty a jejich praktický význam klesá.
Vztah (7.21) je mimořádně důležitý. Tvoří můstek mezi fenomenologickým a strukturním popisem stavového chování plynu. Z experimentálních dat můžeme stanovit druhý viriální koeficient a porovnat jeho hodnotu s hodnotou stanovenou ze vztahu (7.21). Užívá se zpravidla následujícího postupu. Pro konstantní teploty se vypočítá veličina (z - 1)Vm a vynese se v závislosti na 1/Vm. V oblasti nízkých hustot, kde současný výskyt tří molekul v malém prostoru jejich vzájemného silového působení je nepravděpodobný, bychom měli dostat přímku. Její úsek na ose (z - 1)Vm udává hodnotu druhého viriálního koeficientu. Na základě zjištěného rozdílu ve stanovených hodnotách druhého viriálního koeficientu se korigují veličiny určující energii vzájemného mezimolekulárního působení.