4.2 Carnotův (ideální) kruhový děj

Carnotův kruhový děj se skládá ze dvou izotermických a ze dvou adiabatických dějů tvořících čtyři dílčí vratné děje.

Zobrazit doplňující text

Přitom budeme předpokládat, že pracovní látkou je ideální plyn uzavřený ve válci s pohyblivým pístem (obr. 4-1). Stěny válce i píst jsou vyrobeny z materiálu, který je ideálním tepelným izolantem (na obrázku šrafováno). Naopak dno válce je zhotoveno z ideálního tepelného vodiče (na obrázku vyznačeno plně), aby mohlo zprostředkovat dokonalou tepelnou výměnu vedením, a sice mezi plynem a ohřívačem O, popřípadě chladičem Ch. K uskutečnění adiabatického děje se dno válce dá zvenčí zakrýt dokonalou tepelnou vložkou TV.

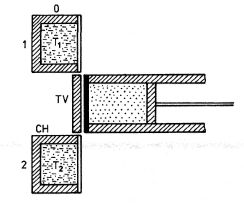Obr. 4-1

Při odvození účinnosti Carnotova cyklu probereme postupně čtyři děje na sebe navzájem navazující a probíhající s ideálním plynem stálého látkového množství n. Jednotlivé děje znázorníme v pracovním diagramu p,V - obr. 4-4. Vyjdeme ze stavu znázorněného v diagramu bodem A.

a) Izotermická expanze Plyn má počáteční objem V₁, tlak p₁ a termodynamickou teplotu T₁ . Izotermickou expanzí A

B přejde plyn do stavu B, čímž zvětší svůj objem na hodnotu V₂ a sníží tlak na hodnotu p₂ při nezměněné teplotě T₁. Plyn odebere ohřívači teplo Q₁ a vykoná práci W'₁

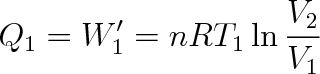(a)

b) Adiabatická expanze . Adiabatickou expanzí (B C) přejde plyn do stavu zobrazeného bodem C. Děj proběhne tak, že plyn zvětšuje svůj objem až na hodnotu V₃, sníží

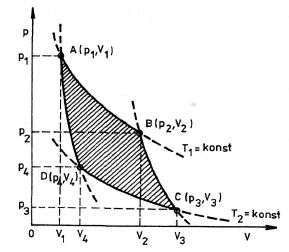Obr. 4-4

tlak na hodnotu p₃ a ochladí se na teplotu T₂ . Plyn koná práci W'₂ na úkor své vnitřní energie, přičemž podle prvního termodynamického zákona (při Q = 0) a užitím vztahu (3.24a) platí

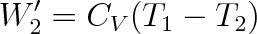(b)

Mezi veličinami T₁, V₂, T₂ a V₃ platí podle (3.38)

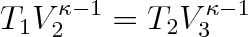(b)

c) Izotermická komprese Plyn izotermicky stlačujeme při teplotě T₂ až do stavu znázorněného bodem D. Plyn odevzdá chladiči teplo Q'₂, jeho objem se zmenší z V₃ na V₄a tlak vzroste z hodnoty p₃ na hodnotu p₄. Vynaložená práce W₃ vnějších sil je dána podle (3.35) a (3.33) vztahem

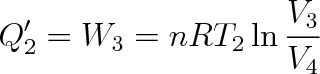(c)

d) Adiabatická komprese Plyn adiabatickou kompresí (D A) převedeme do počátečního stavu A. Touto kompresí se zmenší objem plynu z V₄ na V₁, tlak se zvýší z p₃ na p₁a teplota vzroste na teplotu ohřívače T₁ Cyklus je uzavřen. Práce W₄ vnějších sil je dána vztahem

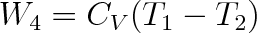(d)

Mezi veličinami T₂, V₄, T₁, V₁ platí Poissonův zákon ve tvaru (3.38), takže

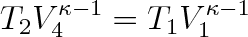(d)

Nyní provedeme energetickou bilanci celého cyklu. Celkovou práci W' vykonanou plynem vyjádříme vztahem

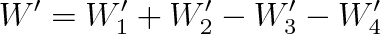a dosazením vztahů (a) až (d) dostaneme

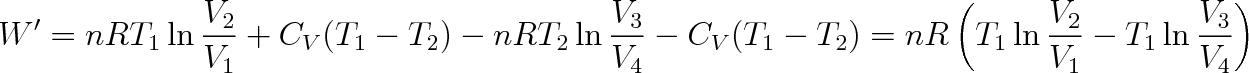(e)

Z podmínek (b') a (d') dostaneme po jednoduché úpravě vztah pro objemy

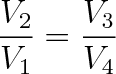(f)

který ukazuje, že poměr, v němž plyn při izotermické expanzi svůj objem

zvětšuje, je týž, v jakém jej zmenšuje při izotermické kompresi. Dosadíme-li podmínku (f) do vztahu (e), dostaneme

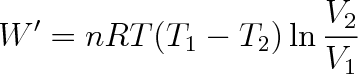(4.3)

Protože T₁ > T₂ a V₂ > V₁, je také W' > 0. Tím rovnice (4.3) dokazuje, že Carnotův kruhový děj končí pracovním ziskem. Tento pracovní zisk je vyjádřen hodnotou vykonané práce W', pro kterou platí vztah (4.3). Graficky je tato hodnota znázorněna obsahem vyšrafované plochy ABCDA na obr. 4-4.

Dosadíme-li vztahy (4.3) a (a) do vztahu (4.2), dostaneme po úpravě vztah pro účinnost 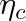Carnotova cyklu

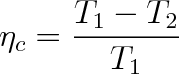(4.4)

Účinnost Carnotova cyklu závisí pouze na teplotách ohřívače a chladiče a je vždy menší než 1 . Je mořno dokázat, že p ředstavuje maximální účinnost, které může tepelný motor pracující mezi lázněmi o teplotách T₁ a T₂ dosáhnout.

Zobrazit doplňující text

Má-li např. přehřátá vodní pára vstupující do trysek parní turbíny teplotu 800 K a pára vystupující teplotu 300 K, je 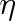= 500/800 0,62, tj. 62 %. Pro nevratnost dějů probíhajících v turbíně a vzhledem k dalším ztrátám energie se dosahuje účinnosti poloviční, tj. na uvedeném příkladě asi 30 %. Je zřejmé, že reálný tepelný motor bude dokonalejší, čím menší bude rozdíl mezi skutečně naměřenou účinností a účinností Carnotova cyklu mezi týmiž teplotami a vypočtenou podle vztahu (4.4)