Mějme sílu
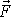 působící v bodě B. Poloha bodu B je
dána polohovým vektorem
působící v bodě B. Poloha bodu B je
dána polohovým vektorem
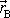 . Dále mějme bod A, jehož poloha je dána vektorem
. Dále mějme bod A, jehož poloha je dána vektorem
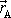 (viz obr.13).
Momentem
(viz obr.13).
Momentem
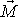 síly
síly
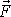 vůči bodu A nazýváme výraz
vůči bodu A nazýváme výraz
 Velikost vektoru
Velikost vektoru
 , tj. výraz
, tj. výraz
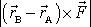 odpovídá elementární [1] definici momentu síly,
která moment zavádí jako součin velikosti a ramene síly. Velikost vektoru
odpovídá elementární [1] definici momentu síly,
která moment zavádí jako součin velikosti a ramene síly. Velikost vektoru
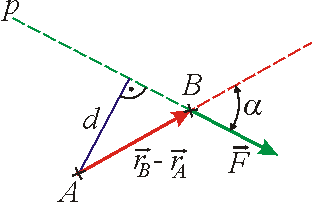
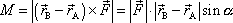 , , |
 kde a
je úhel mezi kladnými směry vektorů
kde a
je úhel mezi kladnými směry vektorů
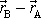 a
a
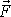 (viz obr.14). Uvědomíme-li si rovnost
vrcholových úhlů, je z obr.14 zřejmé, že
(viz obr.14). Uvědomíme-li si rovnost
vrcholových úhlů, je z obr.14 zřejmé, že
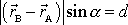 . Symbolem d
je označena kolmá
vzdálenost bodu A od přímky p
, v níž působí síla
. Symbolem d
je označena kolmá
vzdálenost bodu A od přímky p
, v níž působí síla
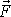 , tedy ta veličina, která bývá nazývána ramenem síly.
, tedy ta veličina, která bývá nazývána ramenem síly.
Rozšíření
elementární definice, která zavádí moment síly jakožto vektor určený výrazem
(3,32)
, umožní rozlišit různě prostorově orientované momenty sil. Moment síly
zavedený definiční rovnicí
(3,32)
je vektor kolmý na rovinu určenou
vektory
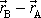 a
a
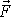 . Je-li soustava souřadnic, v které vekto-rový součin vyjadřujeme, soustavou
pravo-točivou, tvoří vektory
. Je-li soustava souřadnic, v které vekto-rový součin vyjadřujeme, soustavou
pravo-točivou, tvoří vektory
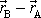 ,
,
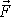 a
a
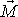 v uvedeném pořadí pravotočivý systém.
v uvedeném pořadí pravotočivý systém.
Obdobně
jako moment síly zavádíme i moment hybnosti. Hmotný bod, jehož hybnost je
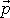 , se nachází v bodě B o polohovém vektoru
, se nachází v bodě B o polohovém vektoru
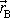 .
Momentem hybnosti
.
Momentem hybnosti
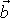 tohoto hmotného bodu vůči bodu A, jehož
polohový vektor je
tohoto hmotného bodu vůči bodu A, jehož
polohový vektor je
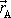 , nazveme výraz
, nazveme výraz
Určujeme-li moment síly působící v místě o polohovém
vektoru
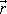 vůči počátku soustavy souřadnic, zjednoduší
se výraz
(3,32)
na tvar
vůči počátku soustavy souřadnic, zjednoduší
se výraz
(3,32)
na tvar
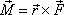 . . |
(3,34) |
Obdobně, nachází-li se hmotný bod o hybnosti
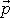 v místě o polohovém vektoru
v místě o polohovém vektoru
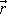 a zjišťujeme-li jeho moment hybnosti vůči
počátku soustavy souřadnic, zjednoduší se výraz
(3,33)
na tvar
a zjišťujeme-li jeho moment hybnosti vůči
počátku soustavy souřadnic, zjednoduší se výraz
(3,33)
na tvar
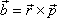 . . |
(3,35) |
Působí-li na hmotný bod síla
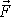 , jsou moment
, jsou moment
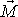 této síly a moment hybnosti
této síly a moment hybnosti
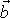 hmotného bodu počítané vůči témuž
vztaženému bodu vázány rovnicí
hmotného bodu počítané vůči témuž
vztaženému bodu vázány rovnicí
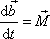 . . |
(3,36) |
Důkaz tvrzení
(3,36)
se provádí přímým výpočtem výrazu
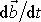 .
.
Z definice
(3,33)
vektoru
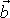 a z pravidla o derivaci vektorového
součinu (např. [24], kap.7) plyne
a z pravidla o derivaci vektorového
součinu (např. [24], kap.7) plyne
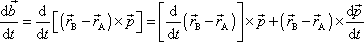 . . |
(3,37) |
Polohu vztažného bodu A budeme pokládat za stálou a tedy
vektor
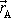 za časově konstantní vektor. Potom
za časově konstantní vektor. Potom
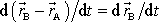 . Výraz
. Výraz
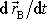 značí rychlost, s jakou se mění poloha
bodu B, tedy rychlost
značí rychlost, s jakou se mění poloha
bodu B, tedy rychlost
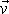 hmotného bodu. Hybnost
hmotného bodu. Hybnost
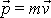 , a tedy
, a tedy
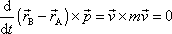 . . |
Jakožto vektorový součin dvou rovnoběžných vektorů je člen
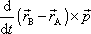 |
z rovnice
(3,37)
nulový. Dle rovnice
(3,29)
je
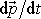 rovno síle
rovno síle
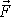 působící na hmotný bod, tedy
působící na hmotný bod, tedy
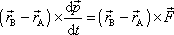 |
a pro hledanou hodnotu
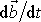 dostáváme z rovnice
(3,37)
dostáváme z rovnice
(3,37)
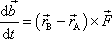 . . |
Výraz na pravé straně poslední rovnice je však dle definice
(3,33)
momentem síly
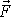 vůči bodu A, čímž je důkaz tvrzení
(3,36)
proveden.
vůči bodu A, čímž je důkaz tvrzení
(3,36)
proveden.
zavři