Hybností
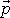 hmotného bodu nazýváme součin jeho
hmotnosti m
a rychlosti
hmotného bodu nazýváme součin jeho
hmotnosti m
a rychlosti
 :
:
Pro vystižení časového účinku
síly se zavádí další veličina impuls síly
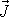 .
Impuls
.
Impuls
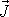 síly
síly
 , která působí na hmotný bod po časový interval
, která působí na hmotný bod po časový interval
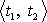 , je definován určitým integrálem
, je definován určitým integrálem
Impuls a hybnost jsou vázány vztahem:
V rovnici
(3,28)
je
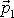 hybnost hmotného bodu v čase
hybnost hmotného bodu v čase
 , od kterého začala působit síla
, od kterého začala působit síla
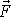 vytvářející impuls
vytvářející impuls
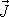 a
a
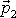 hybnost hmotného bodu v čase
hybnost hmotného bodu v čase
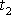 , kdy přestala působit síla
, kdy přestala působit síla
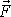 . Při
důkazu tvrzení
(3,28)
se vychází z druhého Newtonova zákona
(2,1)
.
. Při
důkazu tvrzení
(3,28)
se vychází z druhého Newtonova zákona
(2,1)
.
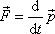 . . |
(3,29) |
Dle
(2,1)
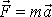 a předpokládáme-li ve shodě
s Newtonovou mechanikou, že hmotnost
m hmotného bodu je konstantní, potom
a předpokládáme-li ve shodě
s Newtonovou mechanikou, že hmotnost
m hmotného bodu je konstantní, potom
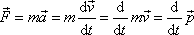 . . |
Dosadíme-li do definiční rovnice impulsu
(3,27)
vyjádření
síly
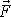 dle
(3,29)
, dostáváme
dle
(3,29)
, dostáváme
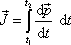 |
, odkud bezprostředně plyne dokazovaný vztah
 .
.
Pojem impulsu
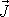 síly je důležitý pro vyšetřování dějů, u
kterých lze obtížně stanovit a není důležitý přesný časový průběh síly, ale
pouze její úhrnný efekt . Příkladem takových dějů je pohyb střely v hlavni
střelné zbraně. Počáteční hybnost
síly je důležitý pro vyšetřování dějů, u
kterých lze obtížně stanovit a není důležitý přesný časový průběh síly, ale
pouze její úhrnný efekt . Příkladem takových dějů je pohyb střely v hlavni
střelné zbraně. Počáteční hybnost
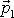 střely je nulová, hybnost
střely je nulová, hybnost
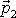 při opuštění hlavně lze určit
z rychlosti střely a z její známé hmotnosti. Z rozdílu
hybností
při opuštění hlavně lze určit
z rychlosti střely a z její známé hmotnosti. Z rozdílu
hybností
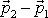 určíme dle rovnice
(3,28)
impuls síly, který
na střelu v hlavni působil. Určit detailní průběh sil působících na střelu
v hlavni by bylo podstatně obtížnější a pro řešení řady úloh není takové
detailní určení nutné. Obdobně, odráží-li se míč od stěny, můžeme z rozdílu
hybností míče před dopadem na stěnu a po odražení od stěny určit impuls síly,
který stěna míči udělila, aniž bychom museli zkoumat časový průběh sil
působících mezi míčem a stěnou.
určíme dle rovnice
(3,28)
impuls síly, který
na střelu v hlavni působil. Určit detailní průběh sil působících na střelu
v hlavni by bylo podstatně obtížnější a pro řešení řady úloh není takové
detailní určení nutné. Obdobně, odráží-li se míč od stěny, můžeme z rozdílu
hybností míče před dopadem na stěnu a po odražení od stěny určit impuls síly,
který stěna míči udělila, aniž bychom museli zkoumat časový průběh sil
působících mezi míčem a stěnou.
Místo skutečné síly
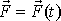 vytvářející impuls
vytvářející impuls
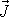 uvažujeme někdy konstantní průměrnou sílu
uvažujeme někdy konstantní průměrnou sílu
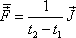 . . |
(3,30) |
Vzorec
(3,30)
vystihuje přirozeně požadovanou vlastnost
průměrné síly
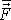 , aby tato síla udělila hmotnému bodu za stejný časový interval stejný impuls
jako skutečně působící časově proměnná síla
, aby tato síla udělila hmotnému bodu za stejný časový interval stejný impuls
jako skutečně působící časově proměnná síla
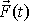 . Průměrná síla
. Průměrná síla
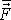 je zavedena tak, jak odpovídá zavedení
průměrných hodnot závisle proměnných veličin v určitém intervalu nezávisle
proměnné. Nezávislou proměnnou je zde čas
je zavedena tak, jak odpovídá zavedení
průměrných hodnot závisle proměnných veličin v určitém intervalu nezávisle
proměnné. Nezávislou proměnnou je zde čas
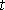 , závisle proměnnou síla
, závisle proměnnou síla
 a rovnice
(3,30)
po rozepsání výrazu pro
impuls
a rovnice
(3,30)
po rozepsání výrazu pro
impuls
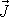 dává
dává
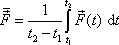 . . |
(3,31) |
Jako příklad nyní vypočítáme průměrnou sílu
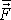 , kterou působí stěna na míč hmotnosti
, kterou působí stěna na míč hmotnosti
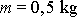 , dopadá-li míč na stěnu kolmo rychlostí o velikosti
, dopadá-li míč na stěnu kolmo rychlostí o velikosti
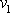 = 5 m/s a odráží se od ní též kolmo rychlostí o velikosti
v 2 = 4,5 m/s.
Doba styku míče a stěny
= 5 m/s a odráží se od ní též kolmo rychlostí o velikosti
v 2 = 4,5 m/s.
Doba styku míče a stěny
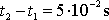 . Z uvedených údajů pro hledanou průměrnou sílu dostáváme vyjádření
. Z uvedených údajů pro hledanou průměrnou sílu dostáváme vyjádření
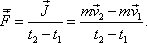 |
Průměrná síla
 má směr kolmý ke stěně, míří od stěny a její
velikost je
má směr kolmý ke stěně, míří od stěny a její
velikost je
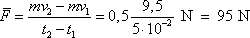 . . |
zavři