Klasifikace dle tvaru dráhy:
Pohyb bodu, který se děje po přímce, nazýváme
přímočarým
. Pohyb, který se neděje po přímce, nazýváme
křivočarým
.
Klasifikace dle velikosti vektoru rychlosti:
Je-li velikost vektoru rychlosti
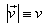 s časem konstantní, nazýváme pohyb
rovnoměrným
.
V opačném případě, tj. když velikost rychlosti se mění s časem,
nazýváme pohyb
nerovnoměrným
.
s časem konstantní, nazýváme pohyb
rovnoměrným
.
V opačném případě, tj. když velikost rychlosti se mění s časem,
nazýváme pohyb
nerovnoměrným
.
Vyšetřujeme-li přímočaré pohyby, můžeme s výjimkou případů, kdy sledujeme vzájemné chování více pohybů, které se dějí po různoběžkách nebo mimoběžkách položit jednu ze souřadnicových os do přímky, v které se pohyb děje. Místo tří parametrických rovnic (1,3) popisujících obecný pohyb stačí pak rovnice jediná, kterou označíme
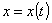 . . |
(1,20) |
Často se pro označení dráhy užívá písmeno s. Pro časovou závislost dráhy bodu na čase pak píšeme vyjádření s=s(t), které pro přímočaré pohyby je ekvivalentní s vyjádřením (1,20) .
zavři
Přímočarý rovnoměrný pohyb
Nejobecnější parametrická rovnice
(1,20)
pro vyjádření
přímočarého rovnoměrného pohybu má tvar
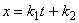 , , |
(1,21) |
kde k1 a k2
jsou konstanty. Rychlost pohybu
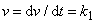 , a tedy první z konstant udává rychlost pohybu, která
je zřejmě konstantní. Druhá konstanta k2
udává polohu bodu v čase t =0. Současný požadavek
rovnoměrnosti a přímočarosti pohybu vymezí tedy zcela určitý pohyb, který
popíšeme parametrickou rovnicí
(1,21)
, proložíme-li přímkou, v níž pohyb
probíhá, souřadnicovou osu x.
, a tedy první z konstant udává rychlost pohybu, která
je zřejmě konstantní. Druhá konstanta k2
udává polohu bodu v čase t =0. Současný požadavek
rovnoměrnosti a přímočarosti pohybu vymezí tedy zcela určitý pohyb, který
popíšeme parametrickou rovnicí
(1,21)
, proložíme-li přímkou, v níž pohyb
probíhá, souřadnicovou osu x.
zavři
Přímočaré nerovnoměrné pohyby
Přímočarým nerovnoměrným je každý pohyb, který probíhá
v přímce s výjimkou pohybu popsaného rovnicí
(1,21)
. Vymyslíme-li si
nějakou obecnou funkci x = x(t), např.
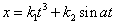 , , |
kde
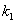 ,
,
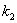 ,
,
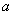 jsou konstanty, bude
pohyb popsaný takovou funkcí pohybem přímočarým nerovnoměrným. Lze se o tom
přesvědčit, vypočteme-li rychlost pohybu. Pro námi zvolený příklad dostáváme
jsou konstanty, bude
pohyb popsaný takovou funkcí pohybem přímočarým nerovnoměrným. Lze se o tom
přesvědčit, vypočteme-li rychlost pohybu. Pro námi zvolený příklad dostáváme
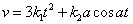 , , |
a tedy velikost rychlosti v zřejmě není s časem konstantní.
Máme-li jedinou parametrickou rovnici x=x
(t), označujeme jí příslušnou složku rychlosti symbolem
v bez indexu. Tato složka má kladnou hodnotu, když rychlost
míří ve směru kladné orientace osy
x, míří-li proti ní, má hodnotu zápornou. Symbolem
v se však také zkráceně označuje velikost vektoru
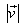 . Mezi oběma pojmy je nutno přísně rozlišovat. Protože
v přímce má vektor jedinou složku, označuje se někdy tato složka jako
vektor v přímce. U všech vektorů, nejen u vektoru rychlosti, musíme přísně
rozlišovat mezi velikostí vektoru, která může být jen kladná a vektorem
v přímce, který může být kladný i záporný. Bohužel běžně užívaná symbolika
tyto dva odlišné pojmy označuje stejně.
. Mezi oběma pojmy je nutno přísně rozlišovat. Protože
v přímce má vektor jedinou složku, označuje se někdy tato složka jako
vektor v přímce. U všech vektorů, nejen u vektoru rychlosti, musíme přísně
rozlišovat mezi velikostí vektoru, která může být jen kladná a vektorem
v přímce, který může být kladný i záporný. Bohužel běžně užívaná symbolika
tyto dva odlišné pojmy označuje stejně.
Z nerovnoměrných přímočarých pohybů podrobněji vyšetříme dva pohyb rovnoměrně zrychlený a pohyb harmonický.
Pohyb přímočarý rovnoměrně zrychlený
Jako přímočarý rovnoměrně zrychlený označujeme pohyb, který
se děje po přímce a který má konstantní zrychlení. Takový pohyb je obecně
popsán parametrickou rovnicí
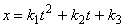 , , |
(1,22) |
kde k1, k2, k3 jsou konstanty. Rychlost pohybu
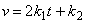 |
(1,23) |
a zrychlení
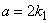 . . |
(1,24) |
Z rovnice (1,24) plyne, že konstanta k1=a/2. Význam konstanty k2 získáme z rovnice (1,23) , položíme-li čas t =0. Konstanta k2 je rovna rychlosti bodu v čase t =0, tedy tzv. počáteční rychlost bodu, kterou značíme v0. Stejným způsobem zjistíme, že konstanta k3 má význam polohy bodu v čase t =0, kterou značíme x0. Dosadíme-li do rovnice (1,22) význam konstant ki, můžeme ji přepsat na obvyklý tvar rovnice rovnoměrně zrychleného pohybu:
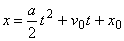 . . |
(1,22´) |
V případě, že zrychlení je záporné, a<0, se někdy pohyb popsaný rovnicí (1,22´) označuje jako rovnoměrně zpožděný.
Harmonický pohyb
Harmonickým nazýváme takový pohyb bodu, pro který závislost
polohy bodu na čase je dána harmonickou funkcí, tj. funkcí kosinus, sinus nebo
jejich lineární kombinací. Použijeme-li zápisu užívajícího funkci sinus,
zapíšeme harmonický pohyb probíhající podél přímky, kterou jsme proložili
osu x, v tvaru
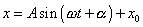 . . |
(1,25) |
V rovnici
(1,25)
harmonického pohybu, který bývá též nazýván
harmonickým kmitem, užíváme pro kladnou konstantu
A (A>0)
označení amplituda kmitu a pro výraz
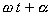 fáze kmitu. Kladná konstanta w (w > 0)
se nazývá kruhová nebo též úhlová frekvence
a konstanta a fázová konstanta (počáteční fáze).
Koná-li bod harmonický kmit
(1,25)
, pohybuje se pouze po úsečce
fáze kmitu. Kladná konstanta w (w > 0)
se nazývá kruhová nebo též úhlová frekvence
a konstanta a fázová konstanta (počáteční fáze).
Koná-li bod harmonický kmit
(1,25)
, pohybuje se pouze po úsečce
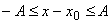 . Střed této úsečky, který leží v bodě x0,
se nazývá rovnovážná poloha bodu. Při vyšetřování
harmonického pohybu se často klade počátek souřadnicové osy,
tj. bod x=0, do rovnovážné polohy kmitajícího bodu. Potom je
. Střed této úsečky, který leží v bodě x0,
se nazývá rovnovážná poloha bodu. Při vyšetřování
harmonického pohybu se často klade počátek souřadnicové osy,
tj. bod x=0, do rovnovážné polohy kmitajícího bodu. Potom je
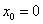 .
.
Harmonický kmit je pohybem periodickým. Po době (časovém intervalu)
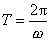 , , |
(1,26) |
kterou nazýváme dobou kmitu , se celý průběh pohybu opakuje. Převrácená hodnota doby kmitu udává kolik kmitů bod vykoná za jednotku času. Tuto veličinu nazýváme frekvencí
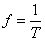 |
(1,27) |
a její vztah k úhlové frekvenci w plyne z rovnice (1,26)
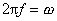 . . |
(1,28) |
Použijeme-li vzorce
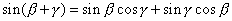 k úpravě výrazu
(1,25)
, dostáváme
k úpravě výrazu
(1,25)
, dostáváme
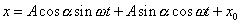 . . |
Výrazy
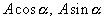 jsou konstantní a
můžeme je označit postupně c ,d.
S tímto označením přejde rovnice
(1,25)
na ekvivalentní tvar
jsou konstantní a
můžeme je označit postupně c ,d.
S tímto označením přejde rovnice
(1,25)
na ekvivalentní tvar
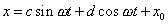 , , |
(1,29) |
který bývá pro vyjádření harmonického pohybu také užíván.
Harmonický pohyb je rovnicí
(1,29)
vyjádřen jako součet
harmonických funkcí
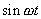 a
a
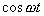 s různými koeficienty c a d.
Pro vzájemný přepočet vyjádření
(1,25)
a
(1,29)
harmonického pohybu zřejmě
platí vzorce
s různými koeficienty c a d.
Pro vzájemný přepočet vyjádření
(1,25)
a
(1,29)
harmonického pohybu zřejmě
platí vzorce
 . . |
(1,30) |
Vyjdeme-li ze zápisu harmonického pohybu ve tvaru (1,25) , dostáváme jeho derivací (srov. rov. (1,11) ) pro rychlost harmonického pohybu vyjádření
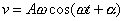 . . |
(1,31) |
Dalším derivováním (srov. rov. (1,14) ) pak získáme zrychlení harmonického pohybu ;
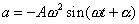 . . |
(1,32) |
Rychlost v a zrychlení a v rovnicích (1,31) a (1,32) jsou vektory v přímce x (v průběhu času nabývají kladných i záporných hodnot) a nesmějí být zaměňovány s velikostí vektorů rychlosti a zrychlení (velikost vektoru je kladná hodnota nebo nula), i když pro ně bývá užíván stejný symbol. (Srovnej s poznámkou pod čarou na stránce 19.)
Rychlost i zrychlení harmonického pohybu jsou opět
harmonickými funkcemi času. Velikost rychlosti má maximální hodnotu
v rovnovážné poloze, velikost zrychlení je maximální v krajních
polohách pohybu. Porovnáme-li rovnici
(1,32)
s rovnicí
(1,25)
, dostáváme
důležitý vztah mezi zrychlením a a výchylkou
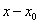 harmonického pohybu:
harmonického pohybu:
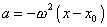 |
(1,33) |
Zrychlení harmonického pohybu je úměrné výchylce a míří proti
ní, konstantou úměrnosti je kladná veličina čtverec úhlové frekvence
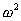 .
.
zavři
Jako křivočaré označujeme pohyby, které se nekonají po přímce. Zůstává-li bod, který koná křivočarý pohyb, stále v jedné rovině, můžeme jej v této rovině popěma parametrickými rovnicemi
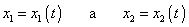 . . |
Takový pohyb označujeme jako rovinný křivočarý pohyb. Příkladem takových pohybů jsou dále probírané pohyby po kružnici rovnoměrný a nerovnoměrný kruhový pohyb. Pohybuje-li se bod v celém prostoru, např. pohybuje-li se po šroubovici, musíme k jeho popisu použít všech tří parametrických rovnic (1,3) .
zavři
Křivočaré rovnoměrné pohyby
Jsou to pohyby, které se nekonají po přímce, ale velikost
rychlosti při nich zůstává stálá. Vektor rychlosti bodu konajícího takový pohyb
mění pouze svůj směr, ale nemění svou velikost. Nejznámějším pohybem tohoto
druhu je rovnoměrný pohyb po kružnici, který běžně nazýváme rovnoměrný kruhový
pohyb.
Rovnoměrný kruhový pohyb
Trajektorie tohoto pohybu je popsána parametrickými
rovnicemi
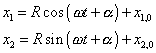 . . |
(1,34) |
Veličiny R>0, w, a,
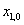 ,
,
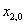 jsou konstanty.
Dráhu pohybu (srov. stať 1.2.4) určíme, když z rovnic
(1,34)
vyloučíme
proměnný parametr t (čas). Postup je takový,
že nejprve převedeme konstanty
jsou konstanty.
Dráhu pohybu (srov. stať 1.2.4) určíme, když z rovnic
(1,34)
vyloučíme
proměnný parametr t (čas). Postup je takový,
že nejprve převedeme konstanty
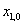 a
a
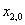 na levou stranu
rovnic, pak obě rovnice umocníme na druhou a sečteme je. Dostaneme rovnici kružnice
na levou stranu
rovnic, pak obě rovnice umocníme na druhou a sečteme je. Dostaneme rovnici kružnice
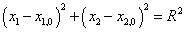 . . |
(1,35) |
Drahou pohybu je tedy kružnice o poloměru R
se středem v bodě o souřadnicích
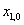 ,
,
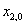 . Fázová konstanta (počáteční fáze) určuje polohu bodu
v čase
. Fázová konstanta (počáteční fáze) určuje polohu bodu
v čase
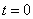 .
.
Rychlost
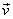 pohybu má složky,
které vypočteme derivací rovnic
(1,34)
(srov. rovnice
(1,11)
)
pohybu má složky,
které vypočteme derivací rovnic
(1,34)
(srov. rovnice
(1,11)
)
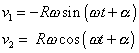 |
(1,36) |
Velikost rychlosti
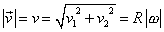 |
(1,37) |
Rovnice
(1,37)
ukazuje, že
velikost rychlosti v je konstantní, a tedy
pohyb je rovnoměrný. Je podobná rovnici
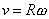 známé ze středoškolského výkladu jako rovnice, která udává vztah mezi
postupnou rychlostí v a úhlovou rychlostí
w kruhového
pohybu. Úhlová i postupná rychlost mohou být jak kladné, tak i záporné.
Znaménko udává, v jakém smyslu bod po kružnici obíhá (ve smyslu nebo proti
smyslu oběhu hodinových ručiček). Velikost vektoru může být jen kladná, proto
je v rovnici
(1,37)
úhlová rychlost v absolutní hodnotě.
známé ze středoškolského výkladu jako rovnice, která udává vztah mezi
postupnou rychlostí v a úhlovou rychlostí
w kruhového
pohybu. Úhlová i postupná rychlost mohou být jak kladné, tak i záporné.
Znaménko udává, v jakém smyslu bod po kružnici obíhá (ve smyslu nebo proti
smyslu oběhu hodinových ručiček). Velikost vektoru může být jen kladná, proto
je v rovnici
(1,37)
úhlová rychlost v absolutní hodnotě.
Později, při vyšetřování nerovnoměrného kruhového pohybu, se
setkáme s úhlovou rychlostí, která je funkcí času
;
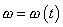 . V čl.2.4 rozšíříme pojem úhlové rychlosti na
vektorovou veličinu
. V čl.2.4 rozšíříme pojem úhlové rychlosti na
vektorovou veličinu
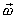 a v kapitole 5
budeme uvažovat časovou závislost
a v kapitole 5
budeme uvažovat časovou závislost
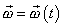 tohoto vektoru.
Úhlová frekvence zavedená rovnicí
(1,25)
a úhlová rychlost jsou tedy různé
veličiny, i když vzhledem k některým analogiím a stejnému fyzikálnímu
rozměru (s 1) bývá pro ně užíván stejný symbol w.
tohoto vektoru.
Úhlová frekvence zavedená rovnicí
(1,25)
a úhlová rychlost jsou tedy různé
veličiny, i když vzhledem k některým analogiím a stejnému fyzikálnímu
rozměru (s 1) bývá pro ně užíván stejný symbol w.
Složky zrychlení
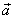 rovnoměrného
kruhového pohybu získáme (srov. rov.
(1,14)
) derivací odpovídajících složek
(1,36)
vektoru rychlosti. Dostaneme
rovnoměrného
kruhového pohybu získáme (srov. rov.
(1,14)
) derivací odpovídajících složek
(1,36)
vektoru rychlosti. Dostaneme
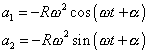 |
(1,38) |
Zavedeme vektor
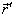 , který má počátek ve středu kružnice
(1,35)
a konec
v místě okamžité polohy bodu konajícího kruhový pohyb
(1,34)
. Složky
vektoru
, který má počátek ve středu kružnice
(1,35)
a konec
v místě okamžité polohy bodu konajícího kruhový pohyb
(1,34)
. Složky
vektoru
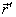 jsou
jsou
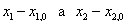 , tedy
, tedy
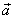 . . |
Porovnáme-li rovnice
(1,38)
a
(1,34)
, vidíme, že mezi
vektory
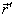 a
a
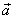 ; platí vztah
; platí vztah
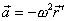 . . |
(1,39) |
Vektor
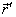 míří od středu
kružnice k místu, kde se nachází bod a zrychlení bodu má dle
rovnice
(1,39)
stejný směr a opačný smysl, míří tedy do středu kružnice.
Proto se mu říká zrychlení dostředivé.
Pro jeho velikost plyne z rovnice
(1,39)
vyjádření
míří od středu
kružnice k místu, kde se nachází bod a zrychlení bodu má dle
rovnice
(1,39)
stejný směr a opačný smysl, míří tedy do středu kružnice.
Proto se mu říká zrychlení dostředivé.
Pro jeho velikost plyne z rovnice
(1,39)
vyjádření
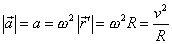 , , |
(1,40) |
kde při úpravách bylo užito skutečnosti, že velikost
vektoru
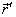 je rovna poloměru
kružnice R
a mezi úhlovou a
postupnou rychlostí platí vztah
(1,37)
.
je rovna poloměru
kružnice R
a mezi úhlovou a
postupnou rychlostí platí vztah
(1,37)
.
Vypočteme-li skalární součin vektorů
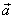 nbsp;
(1,38)
a
nbsp;
(1,38)
a
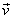 (1,36)
,
dostaneme
(1,36)
,
dostaneme
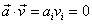 . Vektory
. Vektory
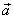 a
a
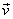 jsou vzájemně kolmé.
Uvědomíme-li si, že rychlost
jsou vzájemně kolmé.
Uvědomíme-li si, že rychlost
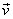 má směr tečny
kružnice a zrychlení
má směr tečny
kružnice a zrychlení
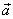 směr poloměru, je
kolmost těchto vektorů zřejmá i z názoru. Tečná složka vektoru zrychlení
je nulová, a proto celkové zrychlení
směr poloměru, je
kolmost těchto vektorů zřejmá i z názoru. Tečná složka vektoru zrychlení
je nulová, a proto celkové zrychlení
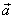 je totožné
s normálovým zrychlením
je totožné
s normálovým zrychlením
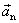 . Tento závěr platí pro všechny rovnoměrné křivočaré pohyby,
protože z jejich charakteristické vlastnosti
. Tento závěr platí pro všechny rovnoměrné křivočaré pohyby,
protože z jejich charakteristické vlastnosti
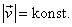 plyne (srov.
rov.
(1,18)
), že tečná složka jejich zrychlení je vždy nulová.
plyne (srov.
rov.
(1,18)
), že tečná složka jejich zrychlení je vždy nulová.
Mezi úhlovou rychlostí w rovnoměrného kruhového pohybu a počtem f , kolikrát bod za jednotku času (sekundu) oběhne kružnici, platí vztah analogický rovnici (1,28)
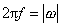 . . |
Veličině f se říká počet obrátek za jednotku času nebo též frekvence kruhového pohybu. Doba T, za kterou bod oběhne kružnici jednou dokola, se nazývá doba oběhu a platí pro ni vztah
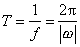 . . |
Rovnoměrný pohyb může bod konat po libovolné křivce. Jako další příklad uvedeme rovnoměrný pohyb po šroubovici . Jeho parametrický popis při vhodném umístění šroubovice je dán rovnicemi
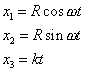 , , |
(1,41) |
kde kromě konstant užitých při popisu rovnoměrného kruhového pohybu je konstantní i veličina k . Důkaz, že rovnice (1,41) popisují pohyb po šroubovici a že pohyb je rovnoměrný, ponecháváme čtenáři.
zavři
Křivočaré nerovnoměrné pohyby
Křivočarý nerovnoměrný pohyb je nejobecnější druh pohybu.
Vybereme-li za parametrické rovnice pohybu libovolné tři funkce
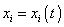 , s největší pravděpodobností pohyb jimi popsaný bude
pohybem křivočarým nerovnoměrným. Z těchto všech možných pohybů podrobněji
popíšeme pouze nerovnoměrný pohyb po kružnici.
, s největší pravděpodobností pohyb jimi popsaný bude
pohybem křivočarým nerovnoměrným. Z těchto všech možných pohybů podrobněji
popíšeme pouze nerovnoměrný pohyb po kružnici.
Nerovnoměrný pohyb po kružnici
Obecný pohyb po kružnici, která má střed v počátku
souřadnicové soustavy, je popsán parametrickými rovnicemi
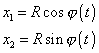 , , |
(1,42) |
kde R je konstanta a j(t) libovolná funkce času t. Umocníme-li obě rovnice na druhou a sečteme je, vypadne nám parametr t a dostaneme rovnici dráhy
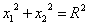 . . |
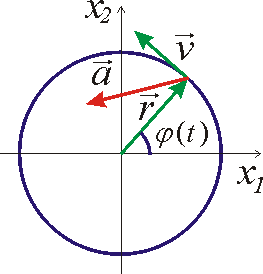
Drahou je tedy zřejmě kružnice o poloměru R.
Funkce j(t) udává, jak rychle bod po kružnici obíhá. Z obr.5 je patrný
její význam. Udává úhel, který svírá polohový vektor
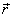 (průvodič) bodu s kladným směrem osy
(průvodič) bodu s kladným směrem osy
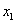 .
.
Rychlost
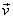 pohybu
(1,42)
má složky
pohybu
(1,42)
má složky
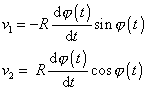 |
(1,43) |
Velikost rychlosti
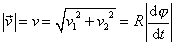 je konstantní pouze,
když výraz
je konstantní pouze,
když výraz
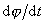 udávající úhlovou rychlost w
pohybu je konstantní (konstantu označíme k). Z podmínky
udávající úhlovou rychlost w
pohybu je konstantní (konstantu označíme k). Z podmínky
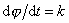 integrací plyne
integrací plyne
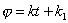 . Pohyb je tedy rovnoměrný, jen když úhel j
je lineární funkcí času. Označíme-li w
konstantu k a a
konstantu
. Pohyb je tedy rovnoměrný, jen když úhel j
je lineární funkcí času. Označíme-li w
konstantu k a a
konstantu
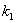 , vidíme, že jde o případ popsaný rovnicemi
(1,34)
, tedy
o rovnoměrný kruhový pohyb podrobněji rozebraný v předcházejícím
odstavci. Pro každou jinou než lineární závislost úhlu j
na čase je pohyb popsaný rovnicemi
(1,42)
pohybem nerovnoměrným. Ovšem i pro nerovnoměrný pohyb udává výraz
, vidíme, že jde o případ popsaný rovnicemi
(1,34)
, tedy
o rovnoměrný kruhový pohyb podrobněji rozebraný v předcházejícím
odstavci. Pro každou jinou než lineární závislost úhlu j
na čase je pohyb popsaný rovnicemi
(1,42)
pohybem nerovnoměrným. Ovšem i pro nerovnoměrný pohyb udává výraz
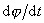 změnu úhlu j
s časem, a tedy úhlovou rychlost
pohybu w.
Rovnice
(1,37)
zůstává v platnosti i pro nerovnoměrný kruhový pohyb,
ovšem w
je obecnou nekonstantní funkcí času t;
změnu úhlu j
s časem, a tedy úhlovou rychlost
pohybu w.
Rovnice
(1,37)
zůstává v platnosti i pro nerovnoměrný kruhový pohyb,
ovšem w
je obecnou nekonstantní funkcí času t;
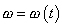 .
.
Drahou obecného pohybu po kružnici nemusí být celá kružnice
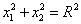 , jako je tomu na obr.5, ale jen její část. Typickým
příkladem takového pohybu je pohyb, který koná koncový bod matematického
kyvadla (viz obr.87 v čl.7.2). Rozbor zde provedený se vztahuje i na případ
matematického kyvadla. Pohyb, při kterém hmotný bod obíhá celou kružnici, bývá
často nazýván nerovnoměrný kruhový pohyb.
, jako je tomu na obr.5, ale jen její část. Typickým
příkladem takového pohybu je pohyb, který koná koncový bod matematického
kyvadla (viz obr.87 v čl.7.2). Rozbor zde provedený se vztahuje i na případ
matematického kyvadla. Pohyb, při kterém hmotný bod obíhá celou kružnici, bývá
často nazýván nerovnoměrný kruhový pohyb.
Složky vektoru zrychlení
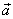 nerovnoměrného kruhového pohybu dostaneme standardním postupem, tj. derivováním rovnic
(1,43)
dle času t. Protože však nyní úhlová
rychlost
nerovnoměrného kruhového pohybu dostaneme standardním postupem, tj. derivováním rovnic
(1,43)
dle času t. Protože však nyní úhlová
rychlost
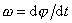 není konstantní, je
výsledek podstatně složitější než v případě
(1,38)
:
není konstantní, je
výsledek podstatně složitější než v případě
(1,38)
:
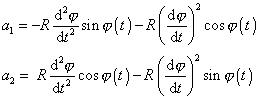 . . |
(1,44) |
Vypočteme-li dle rovnice
(1,15)
složku tečného zrychlení do
směru rychlosti
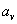 , dostaneme
, dostaneme
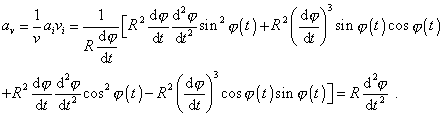 . . |
Předchozí výsledek
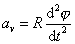 |
můžeme obdržet také podstatně pohodlněji, když dle pravidla
(1,18)
derivujeme rychlost
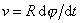 dle času t.
Dle rovnice
(1,16)
je vektor tečné složky zrychlení
dle času t.
Dle rovnice
(1,16)
je vektor tečné složky zrychlení
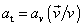 , a tedy
, a tedy
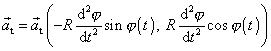 . . |
Vektor normálové složky zrychlení
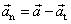 (srov.
(1,17)
).
S přihlédnutím k rovnicím
(1,44)
můžeme pak vektor
(srov.
(1,17)
).
S přihlédnutím k rovnicím
(1,44)
můžeme pak vektor
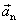 zapsat jako
zapsat jako
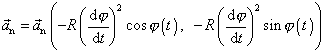 . . |
Srovnáme-li výraz pro
 s rovnicemi
(1,42)
, ověříme si, že vektor
s rovnicemi
(1,42)
, ověříme si, že vektor
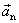 má dostředivý směr míří do středu kružnice, po které se bod pohybuje.
Z vektorového vyjádření normálového zrychlení
má dostředivý směr míří do středu kružnice, po které se bod pohybuje.
Z vektorového vyjádření normálového zrychlení
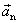 je zřejmé, že jeho velikost
je zřejmé, že jeho velikost
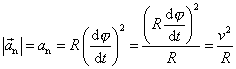 . . |
(1,45) |
Můžeme tak, alespoň pro případ obecného pohybu po kružnici, dokázat platnost rovnice (1,19) .
Porovnáme-li vyjádření vektorů tečného
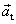 a normálového
a normálového
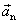 zrychlení s vyjádřením
(1,44)
celkového vektoru zrychlení
zrychlení s vyjádřením
(1,44)
celkového vektoru zrychlení
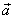 , je patrné, že první sčítance na pravých stranách rovnic
(1,44)
odpovídají složkám vektoru
, je patrné, že první sčítance na pravých stranách rovnic
(1,44)
odpovídají složkám vektoru
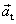 a druhé sčítance složkám vektoru
a druhé sčítance složkám vektoru
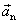 .
.
U nerovnoměrného pohybu po kružnici je tečná složka vektoru
zrychlení
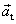 nenulová, a tedy vektor
zrychlení
nenulová, a tedy vektor
zrychlení
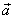 nemíří do středu
kružnice jako jeho normálová složka
nemíří do středu
kružnice jako jeho normálová složka
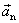 . Vektor zrychlení
. Vektor zrychlení
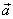 míří obecně do
kruhu, a to buď před průvodič (polohový vektor)
míří obecně do
kruhu, a to buď před průvodič (polohový vektor)
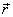 bodu, jako je
znázorněno na obr.5, nebo za tento průvodič.
bodu, jako je
znázorněno na obr.5, nebo za tento průvodič.
zavři