Rovnicemi (1,3) je pohyb bodu zcela popsán. Chceme-li však podrobněji sledovat jednotlivé pohyby a získat kriteria pro jejich rozlišení, je výhodné zavést některé další charakteristiky pohybů. První takovou charakteristikou je rychlost.
Způsob zavedení rychlosti v pro pohyb popsaný rovnicemi (1,5) je všeobecně známý. Stačí vybrat libovolné dva časové okamžiky t1 a t2 , najít jim odpovídající souřadnice x1(t1), x2(t1) a x1(t2), x2(t2) neboli stručně zapsáno xi(t1) a xi(t2), stanovit vzdálenost
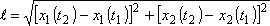 |
poloh xi(t1) a xi(t2) a vydělit ji časovým intervalem t2t1. Tak dostaneme pro rychlost v vyjádření
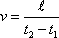 . . |
(1,7) |
Dosadíme-li do rovnice (1,7) konkrétní hodnoty (1,5) , dostáváme
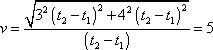 . . |
Rychlost nezávisí na tom, které dva časové okamžiky t2, t1 zvolíme.
Výraz
(1,7)
udává pouze velikost rychlosti. Více informací o daném pohybu získáme,
zavedeme-li rychlost jakožto vektorovou veličinu. Ta kromě velikosti rychlosti
zachytí i směr pohybu bodu. Pro pohyb popsaný rovnicemi
(1,5)
jsou ve zvolené
souřadnicové soustavě složky vektoru rychlosti
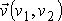 dány výrazy
SETEQS2('knihI10do_soubory/eq0016M.gif','knihI1do_soubory/eq0017M.gif','(1,8)','a','.','2.8','.84');
Lze se snadno přesvědčit, že velikost vektoru
dány výrazy
SETEQS2('knihI10do_soubory/eq0016M.gif','knihI1do_soubory/eq0017M.gif','(1,8)','a','.','2.8','.84');
Lze se snadno přesvědčit, že velikost vektoru
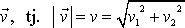 , je rovna výrazu
(1,7)
a že směr vektoru leží
v přímce x2= (4/3)x1, po které
se bod pohybuje. Přitom orientace vektoru odpovídá orientaci pohybu bodu po
přímce.
, je rovna výrazu
(1,7)
a že směr vektoru leží
v přímce x2= (4/3)x1, po které
se bod pohybuje. Přitom orientace vektoru odpovídá orientaci pohybu bodu po
přímce.
V případě pohybu daného rovnicemi
(1,6)
není již způsob
jak zavést rychlost
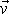 tak zřejmý. Vzdálenosti, které hmotný bod
urazí v různých, byť stejně dlouhých časových intervalech, jsou různé. I
směr pohybu se stále mění. Kdybychom použili k vyjádření složek vektoru
rychlosti rovnic
(1,8)
, dostali bychom výrazy podstatně závislé na volbě
časů t1 a t2
.
Velikost takto zavedeného vektoru je rovna vzdálenosti
bodů xi(t1) a xi(t2),
ve kterých se pohybující bod nachází
v časech t1 a t2, dělené časovým intervalem
tak zřejmý. Vzdálenosti, které hmotný bod
urazí v různých, byť stejně dlouhých časových intervalech, jsou různé. I
směr pohybu se stále mění. Kdybychom použili k vyjádření složek vektoru
rychlosti rovnic
(1,8)
, dostali bychom výrazy podstatně závislé na volbě
časů t1 a t2
.
Velikost takto zavedeného vektoru je rovna vzdálenosti
bodů xi(t1) a xi(t2),
ve kterých se pohybující bod nachází
v časech t1 a t2, dělené časovým intervalem
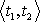 a ne délce dráhy mezi
body xi(t1) a xi(t2) dělené
časovým intervalem. Odhlédneme-li od této skutečnosti, mohli bychom rychlost
zavedenou dle rovnice
(1,8)
pokládat za jakousi průměrnou rychlost
v časovém intervalu
a ne délce dráhy mezi
body xi(t1) a xi(t2) dělené
časovým intervalem. Odhlédneme-li od této skutečnosti, mohli bychom rychlost
zavedenou dle rovnice
(1,8)
pokládat za jakousi průměrnou rychlost
v časovém intervalu
 . Ovšem charakterizovat rychlost pohybu pomocí veličiny, u které bychom museli
udávat interval, ke kterému je nutno ji připisovat, je nevýhodné. Proto se
snažíme zavést pro libovolný pohyb rychlost
. Ovšem charakterizovat rychlost pohybu pomocí veličiny, u které bychom museli
udávat interval, ke kterému je nutno ji připisovat, je nevýhodné. Proto se
snažíme zavést pro libovolný pohyb rychlost
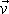 jakožto veličinu, kterou lze přisoudit bodu
v jediném okamžiku, podobně jako je mu rovnicemi
(1,3)
v jediném
okamžiku přiřazena poloha.
jakožto veličinu, kterou lze přisoudit bodu
v jediném okamžiku, podobně jako je mu rovnicemi
(1,3)
v jediném
okamžiku přiřazena poloha.
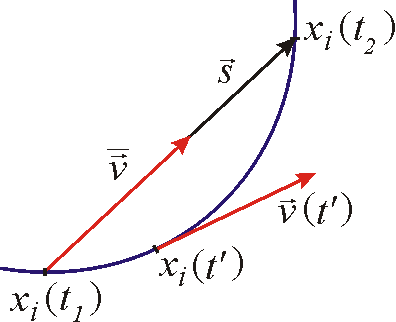
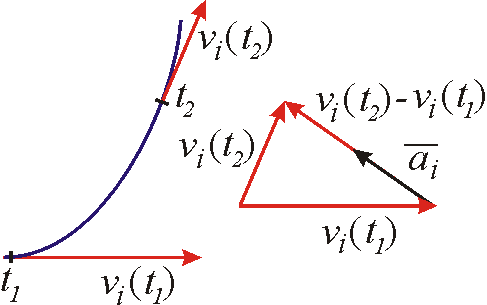
Na obr.3 je
znázorněn úsek dráhy obecného pohybu bodu. Jsou na něm znázorněny polohy
bodu xi(t1)
v čase t1 a xi(t2)
v čase t2. Rozdíly souřadnic
 můžeme pokládat za složky vektoru
můžeme pokládat za složky vektoru
 , jehož počátek je v bodě
, jehož počátek je v bodě
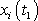 a konec v bodě
a konec v bodě
 . Velikost tohoto vektoru je rovna vzdálenosti mezi body
. Velikost tohoto vektoru je rovna vzdálenosti mezi body
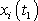 a
a
 . Vydělíme-li vektor
. Vydělíme-li vektor
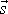 délkou časového intervalu
délkou časového intervalu
 , dostaneme průměrnou rychlost
, dostaneme průměrnou rychlost
 v ča-sovém intervalu v tom smyslu,
v jakém jsme o ní hovořili v předcházejícím odstavci, tj. jako rychlost
po sečně a ne po oblouku dráhy. Použijeme-li složkové symboliky, dostáváme pro
průměrnou rychlost
v ča-sovém intervalu v tom smyslu,
v jakém jsme o ní hovořili v předcházejícím odstavci, tj. jako rychlost
po sečně a ne po oblouku dráhy. Použijeme-li složkové symboliky, dostáváme pro
průměrnou rychlost
 vyjádření odpovídající rovnicím
(1,8)
vyjádření odpovídající rovnicím
(1,8)
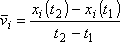 . . |
(1,9) |
Chceme-li nyní dostat rychlost vi jako charakteristiku pohybu vztahující se k jednomu okamžiku t´, je přirozené zavést ji jako limitu výrazu (1,9) , blíží-li se hodnoty t2 a t1 hodnotě t´ (t1 < t´ < t2) ; neboli
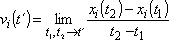 . . |
(1,10) |
V tomto limitním přiblížení vymizí též rozdíly mezi průměrnou rychlostí uvažovanou, tak jak je tomu v rovnici (1,9) jako délka sečny dělená časovým intervalem, a průměrnou rychlostí uvažovanou jako délka skutečné dráhy mezi body xi(t1) a xi(t2) dělená časovým intervalem. Velikost rychlosti podle prvé definice je vždy nejvýše rovná velikosti rychlosti podle druhé z definic, přičemž rovnost nastane pouze, když se pohyb v uvažovaném časovém intervalu děje po přímce.
Limita na pravé straně rovnice (1,10) je definiční limitou pro derivaci funkce xi(t) pro hodnotu nezávisle proměnné t´. Hodnotu t´, pro kterou limitu z rovnice (1,10) počítáme, můžeme zvolit libovolně. Označíme ji tedy t a pro složky rychlosti vi pohybu v čase t budeme s použitím pojmu derivace psát stručné vyjádření
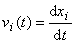 . . |
(1,11) |
Složky vektoru rychlosti jsou derivacemi jim odpovídajících parametrických rovnic (1,3) .
Podobně jako jsme u rovnic (1,2) předpokládali, že popisují křivku, i zde budeme předpokládat, že jsou splněny matematické předpoklady pro existenci derivace. Pro rovnice popisující reálné pohyby je to téměř jisté.
Vypočteme-li dle pravidla (1,11) složky rychlosti v1, v2 a velikost rychlosti v pro pohyb daný rovnicemi (1,5) , dostaneme výsledky shodné s výsledky získanými z rovnic (1,8) a (1,7) .
Tedy rovnice (1,11) jsou rozšířením známého způsobu, jakým byla zavedena rychlost pro rovnoměrný přímočarý pohyb.
Další důležitou charakteristikou pohybu je změna jeho
rychlosti s časem, kterou nazýváme zrychlením. Má-li bod v čase
t1 rychlost vi (t1)
a v čase t2
rychlost vi (t2),
označíme jako průměrné zrychlení
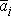 v časovém intervalu <t1, t2>
veličinu (vizobr.4)
v časovém intervalu <t1, t2>
veličinu (vizobr.4)
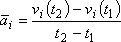 . . |
(1,12) |
Obdobně jako jsme rovnicí (1,10) zavedli okamžitou rychlost vi, zavedeme okamžité zrychlení ai v čase t´ (t1<t´<t2) jako limitu výrazu (1,12)
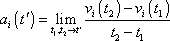 . . |
(1,13) |
Znovu lze uvést, že limita na pravé straně rovnice (1,13) definuje derivaci funkce vi(t) dle času t (derivovat vektor znamená derivovat všechny jeho složky) a čas t´ lze volit libovolně. Tedy vektor zrychlení v čase t je derivací vektoru rychlosti;
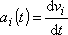 . . |
(1,14) |
Složky vektoru zrychlení jsou derivacemi jim odpovídajících složek vektoru rychlosti.
Popis pohybu bodu, stanovení jeho dráhy, rychlosti a zrychlení jsou základními úkoly kinematiky bodu. Uvedeme schéma, podle kterého lze tyto úkoly plnit:
Pohyb bodu v prostoru popisujeme parametrickými rovnicemi, které, zvolíme-li kartézskou soustavu souřadnic, mají tvar
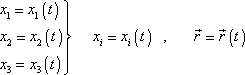 . . |
(1,3) |
V rovnicích
(1,3)
parametr t
znamená čas. Parametrické rovnice xi = xi(t)
popisují trajektorii bodu, tj. jeho dráhu s uvážením času, kdy se
v kterém místě dráhy bod nachází. Poslední rovnice popisuje pohyb bodu
zapsáním časového vývoje jeho polohového vektoru
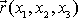 . Tvar dráhy bodu získáme vyloučením parametru t z parametrických rovnic.
. Tvar dráhy bodu získáme vyloučením parametru t z parametrických rovnic.
Rychlost
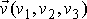 bodu pohybujícího se po trajektorii
(1,3)
určíme derivováním rovnic
(1,3)
dle času t;
bodu pohybujícího se po trajektorii
(1,3)
určíme derivováním rovnic
(1,3)
dle času t;
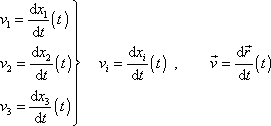 . . |
(1,11) |
Rychlost takto určená je opět funkcí času t. Vypočteme-li dle rovnice (1,3) času t odpovídající polohu xi(t) bodu na trajektorii, můžeme rychlost pokládat i za funkci polohy bodu.
Zrychlení
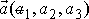 určíme derivováním rovnic
(1,11)
dle času t;
určíme derivováním rovnic
(1,11)
dle času t;
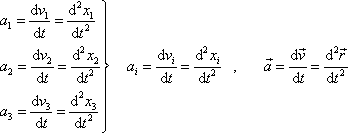 . . |
(1,14) |
Rovnicemi (1,14) je zrychlení určeno jako funkce času t a tedy též času t odpovídající polohy bodu na trajektorii.