Stanovit odolnost látky (materiálu) proti její destrukci je velmi důležitý, ale obtížně řešitelný úkol. Vychází se z normovaných uzančních, tj. dohodou stanovených, zkoušek. Jsou to deformační zkoušky, únavové zkoušky zjišťující odolnost materiálu proti opakovanému namáhání, zkoušky na určení křehkosti, houževnatosti či tvrdosti látky a řada dalších specielnějších technologických zkoušek. Podmínky zkoušek jsou stanoveny normami a popsány např. v [16], [18], [43]. Jako příklad zde popíšeme nejběžnější z těchto zkoušek - deformační zkoušku, při které působícím napětím je tah.
Tahová zkouška se
provádí v trhacím stroji, který je zařízením umožňujícím
provádět deformaci vzorku různými deformačními mechanizmy až po jeho destrukci.
Při tahové zkoušce je vzorek podroben
tahové deformaci, jejíž velikost s časem rovnoměrně roste (rychlost deformace
je konstantní). Sleduje se závislost tahového napětí s na deformaci e. Napětím se zde
rozumí tzv. smluvní napětí, tj.
poměr síly F působící na vzorek k ploše
 průřezu nedeformovaného vzorku;
průřezu nedeformovaného vzorku;
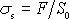 a deformací poměr prodloužení vzorku
a deformací poměr prodloužení vzorku
 k nedeformované (původní) délce vzorku
k nedeformované (původní) délce vzorku
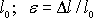 . Upřesnění, o jaké napětí se jedná, je
nutné, protože vzorek je deformován až po svou destrukci - přetržení, kdy
rozdíl mezi původním průřezem a průřezem při přetržení bývá značný. Rozdíl
průřezu nedeformovaného a deformovaného vzorku však obvykle nelze zanedbat již
brzy po začátku tahové zkoušky a nelze tedy užít zjednodušení klasické teorie
pružnosti (kap. 3), která tento rozdíl zanedbává. Deformace při tahové zkoušce
je nutno pokládat za velké deformace (srov. stať 2.1.3) a zavedené smluvní
napětí přísně odlišovat od skutečného aktuálního napětí ve vzorku.
. Upřesnění, o jaké napětí se jedná, je
nutné, protože vzorek je deformován až po svou destrukci - přetržení, kdy
rozdíl mezi původním průřezem a průřezem při přetržení bývá značný. Rozdíl
průřezu nedeformovaného a deformovaného vzorku však obvykle nelze zanedbat již
brzy po začátku tahové zkoušky a nelze tedy užít zjednodušení klasické teorie
pružnosti (kap. 3), která tento rozdíl zanedbává. Deformace při tahové zkoušce
je nutno pokládat za velké deformace (srov. stať 2.1.3) a zavedené smluvní
napětí přísně odlišovat od skutečného aktuálního napětí ve vzorku.
Tvar závislostí
 ,
(2,72)
,
(2,72)
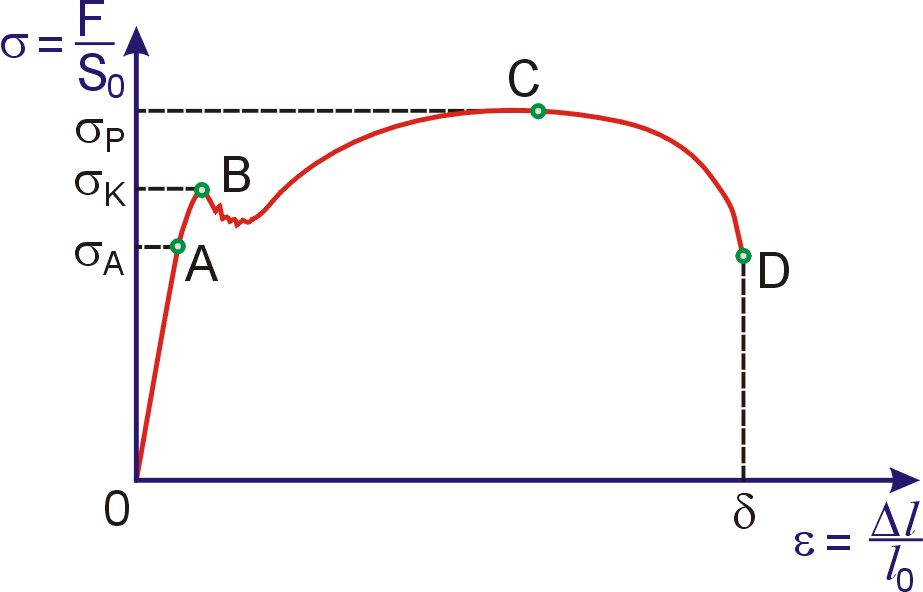
 kterou nazýváme tahová křivka, je pro různé látky různý. Pro řadu kovových
materiálů lze tuto závislost schematicky vystihnout křivkou znázorněnou na
obr.39. (V grafu na obrázku označujeme smluvní napětí stručně s,
aby-chom vyhnuli dvojnásobnému indexování.) Počáteční část křivky až po
bod A
je přímková, napětí je úměrné deformaci, chování materiálu lze
vystihnout modelem hookovské látky. Napětí
kterou nazýváme tahová křivka, je pro různé látky různý. Pro řadu kovových
materiálů lze tuto závislost schematicky vystihnout křivkou znázorněnou na
obr.39. (V grafu na obrázku označujeme smluvní napětí stručně s,
aby-chom vyhnuli dvojnásobnému indexování.) Počáteční část křivky až po
bod A
je přímková, napětí je úměrné deformaci, chování materiálu lze
vystihnout modelem hookovské látky. Napětí
 odpovídající bodu A se označuje jako mez úměrnosti. Překročí-li napětí mez
úměrnosti, může se materiál až po dosažení napětí
odpovídající bodu A se označuje jako mez úměrnosti. Překročí-li napětí mez
úměrnosti, může se materiál až po dosažení napětí
 ,
které odpovídá bodu B
křivky, chovat elasticky (pružně). To znamená, že po odstranění napětí
zaujme svou původní délku
,
které odpovídá bodu B
křivky, chovat elasticky (pružně). To znamená, že po odstranění napětí
zaujme svou původní délku
 ,
jedná se o elastické avšak nelineární chování - mezi body A
a B se vzorek chová jako nelineárně elastická látka (srov. stať 2.1.3
). Napětí
,
jedná se o elastické avšak nelineární chování - mezi body A
a B se vzorek chová jako nelineárně elastická látka (srov. stať 2.1.3
). Napětí
 označujeme jako mez pružnosti nebo též mez elasticity. Po překročení meze pružnosti začne materiál plasticky téct, po
odtížení zůstane trvale deformován (srov. čl.2.4 ).
označujeme jako mez pružnosti nebo též mez elasticity. Po překročení meze pružnosti začne materiál plasticky téct, po
odtížení zůstane trvale deformován (srov. čl.2.4 ).
 U některých materiálů, např. u měkkých
uhlíkatých ocelí se plastický tok projeví zřetelným poklesem napětí (obr.40).
Lokální maximální napětí
U některých materiálů, např. u měkkých
uhlíkatých ocelí se plastický tok projeví zřetelným poklesem napětí (obr.40).
Lokální maximální napětí
 pak jednoznačně určí napětí, při kterém
začíná plastický tok. Takové napětí se označuje jako mez kluzu {yield point}. U materiálů, jejichž tahová křivka
odpovídá obr.39, je stanovení meze kluzu obtížnější. Stanovuje se jako napětí,
pro které trvalá deformace po odtížení dosahuje dohodnuté hodnoty, zpravidla se
volí hodnota 0,2% a odpovídající napětí se označuje jako
mez 0,2.
pak jednoznačně určí napětí, při kterém
začíná plastický tok. Takové napětí se označuje jako mez kluzu {yield point}. U materiálů, jejichž tahová křivka
odpovídá obr.39, je stanovení meze kluzu obtížnější. Stanovuje se jako napětí,
pro které trvalá deformace po odtížení dosahuje dohodnuté hodnoty, zpravidla se
volí hodnota 0,2% a odpovídající napětí se označuje jako
mez 0,2.
Pevnost, též mez pevnosti, látky se určuje jako maximální smluvní napětí dosažené na tahové křivce
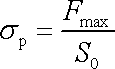 . . |
(2,73) |
Bod maxima křivky je označen C na obou obrázcích (obr.39 a 40). Síla Fmax je maximální síla, kterou je vzorek podrobený tahové zkoušce schopen přenést, S0 je plocha průřezu vzorku před deformací. Po překročení meze pevnosti příčný průřez v některém místě začne prudce klesat, až nakonec se vzorek přetrhne v bodě označeném D.
Z tahové křivky lze odvodit řadu dalších charakteristik vzorku, např. jeho tažnost d zavedenou jako poměr
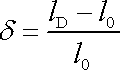 , , |
(2,74) |
kde
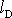 je délka vzorku při přetržení a
je délka vzorku při přetržení a
 jeho původní délka. Při stanovení
pevnostních charakteristik materiálu se neomezujeme jen na tahovou zkoušku.
Materiály se zkouší i v tlaku, smyku (střihu), torzi (krutu) a ohybu.
Získané meze se pak označují i druhem namáhání, při kterém byly získány.
Všechny shora uvedené meze by takto měly atribut "v tahu", např. veličina
stanovená rovnicí
(2,73)
se nazývá mez
pevnosti v tahu.
jeho původní délka. Při stanovení
pevnostních charakteristik materiálu se neomezujeme jen na tahovou zkoušku.
Materiály se zkouší i v tlaku, smyku (střihu), torzi (krutu) a ohybu.
Získané meze se pak označují i druhem namáhání, při kterém byly získány.
Všechny shora uvedené meze by takto měly atribut "v tahu", např. veličina
stanovená rovnicí
(2,73)
se nazývá mez
pevnosti v tahu.
Získané výsledky pevnostních zkoušek, např. získaná hodnota meze pevnosti v tahu zkoušeného materiálu, se při jejich aplikaci násobí činitelem bezpečnosti. Při uvažované tahové zkoušce to znamená, že navrhujeme-li ze zkoušeného materiálu nějakou součástku, hodnota tahového napětí v ní nikde nesmí překročit n-tý díl meze pevnosti. Normou určené číslo n je právě zmíněný činitel bezpečnosti. Jeho velikost určená normou je řádu jednotek až desítek.
Studiem případů destrukce konstrukcí se zjistilo, že někdy ani dodržení pevnostních mezí s bezpečnostními součiniteli destrukci nezabrání. Lom začíná na místě porušení materiálu, na trhlině, v jejímž čele lokální napětí vysoko překračuje průměrné napětí a snadno překročí i hodnotu meze pevnosti materiálu. Zda se trhlina bude šířit celou konstrukcí a dojde k destrukčnímu lomu nebo zda, jak je obvyklé, během šíření trhliny napětí v jejím čele klesne pod kritickou hodnotu a šíření se zastaví, je stěžejní otázkou moderní teorie odolnosti materiálu proti destrukci, která se nazývá lomová mechanika.
Lomová mechanika vychází z
předpokladu, že lokální napětí
 na ose trhliny v okolí jejího čela lze
popsat výrazem
na ose trhliny v okolí jejího čela lze
popsat výrazem
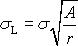 ,
(2,75)
,
(2,75)
 kde A je
konstantní veličina úměrná lineárnímu rozměru trhliny závislá na tvaru trhliny
a způsobu jejího namáhání, s je průměrné napětí v místech dostatečně
vzdálených od trhliny a r
je vzdálenost měřená od čela trhliny ve směru dosud neporušeného vzorku.
Pro trhlinu délky a v tahově
deformovaném vzorku je uvažovaná situace znázorněná na obr.41.
kde A je
konstantní veličina úměrná lineárnímu rozměru trhliny závislá na tvaru trhliny
a způsobu jejího namáhání, s je průměrné napětí v místech dostatečně
vzdálených od trhliny a r
je vzdálenost měřená od čela trhliny ve směru dosud neporušeného vzorku.
Pro trhlinu délky a v tahově
deformovaném vzorku je uvažovaná situace znázorněná na obr.41.
Rovnice (2,75) se přepíše na tvar
 , , |
(2,76) |
kterým je definována veličina K nazývaná součinitel intenzity napětí. Zřejmě platí
 .
(2,77)
.
(2,77)
Hodnota součinitele intenzity napětí a ne hodnota lokálního
napětí
 ,
které pro r (R)
0 neomezeně roste, je v lomové
mechanice užívána jako kriterium pro šíření trhliny.
,
které pro r (R)
0 neomezeně roste, je v lomové
mechanice užívána jako kriterium pro šíření trhliny.
Trhlina se začne šířit, když součinitel intensity napětí K překročí kritickou mez
 a šíření se zastaví, když okamžitá hodnota
součinitele K klesne pod kritickou
hodnotu
a šíření se zastaví, když okamžitá hodnota
součinitele K klesne pod kritickou
hodnotu
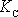 .
.
Blíže se s postupy lomové mechaniky lze seznámit např. v [48] nebo [49]. Obecně o problémech zkoumání vlastností materiálů je pojednáno zábavnější formou v knize [50].