Plastickými nazýváme látky, u nichž tečení (tečením zde nazýváme pohyb, při kterém rychlost deformace D je různá od nuly) nastává až po překročení jisté mezní hodnoty napětí. Plastické vlastnosti vykazují kovy, mnohé makromolekulární látky, laky, stavební materiály a řada dalších látek. V reologické systematice charakterizujeme plastické chování modelem Saint-Venantovým, jehož symbol je znázorněn na obr.35.
Saint-Venantova látka (StV-látka) je modelová látka, která
se pro smykové napětí menší, než je mezní napětí
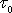 ,
chová jako tuhé těleso a při dosažení mezního napětí
,
chová jako tuhé těleso a při dosažení mezního napětí
 začne téct, přičemž napětí se udržuje na své
mezní hodnotě, kterou nemůže překročit. Chování StV-látky je popsáno rovnicemi
začne téct, přičemž napětí se udržuje na své
mezní hodnotě, kterou nemůže překročit. Chování StV-látky je popsáno rovnicemi
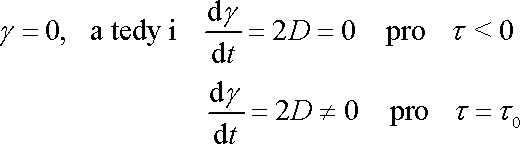 . . |
(2,70) |
 Toto chování vystihuje grafický symbol na
obr.35, který znázorňuje blok spočívající na rovné podložce, přičemž vzájemnému
pohybu bloku a podložky brání síla smykového (vlečného) tření (I4,55) .
Je-li vnější síla snažící se posunout blok vůči podložce menší, než je síla
smykového tření, k pohybu nedojde. Dosáhne-li vnější síla hodnotu
smykového tření, vzájemný pohyb bloku a podložky se uvolní. V StV-modelu
se obvykle pokládá za totožný statický a dynamický součinitel tření, i když někdy,
např. v [19], se
oba druhy tření rozlišují. Kdyby vnější síla byla větší, než je síla tření,
pohyb bloku by byl zrychlený. Tento případ vylučujeme tím, že u StV-modelu
(2,70)
nepředpokládáme, že by
napětí t mohlo být větší než
Toto chování vystihuje grafický symbol na
obr.35, který znázorňuje blok spočívající na rovné podložce, přičemž vzájemnému
pohybu bloku a podložky brání síla smykového (vlečného) tření (I4,55) .
Je-li vnější síla snažící se posunout blok vůči podložce menší, než je síla
smykového tření, k pohybu nedojde. Dosáhne-li vnější síla hodnotu
smykového tření, vzájemný pohyb bloku a podložky se uvolní. V StV-modelu
se obvykle pokládá za totožný statický a dynamický součinitel tření, i když někdy,
např. v [19], se
oba druhy tření rozlišují. Kdyby vnější síla byla větší, než je síla tření,
pohyb bloku by byl zrychlený. Tento případ vylučujeme tím, že u StV-modelu
(2,70)
nepředpokládáme, že by
napětí t mohlo být větší než
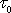 .
Případu
.
Případu
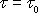 odpovídá rovnost vnější síly a síly tření; blok
se pohybuje konstantní rychlostí, jejíž velikost je určena počátečními
podmínkami pohybu. Volné přecházení mezi pojmy síla a napětí odpovídá pojetí
reologických modelů, jak bylo vyloženo v předcházejícím článku.
odpovídá rovnost vnější síly a síly tření; blok
se pohybuje konstantní rychlostí, jejíž velikost je určena počátečními
podmínkami pohybu. Volné přecházení mezi pojmy síla a napětí odpovídá pojetí
reologických modelů, jak bylo vyloženo v předcházejícím článku.
Předpoklad, že při plastickém toku napětí nepřevyšuje
hodnotu
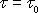 ,
je idealizaci, ale není to předpoklad zcela umělý. Jakmile začne látka
plasticky téct, napětí se v ní nemusí dále zvyšovat. V reálných
plastických látkách může po překročení mezního napětí dojít jak k zvýšení
tak i snížení napětí a přesný popis jejich reologického chování je obtížný.
Přesto, nebo možná právě proto, je v nejpodrobněji vypracované teorii
plasticity, teorii plasticity kovů, StV-model jedním z užívaných modelů
chování látky.
,
je idealizaci, ale není to předpoklad zcela umělý. Jakmile začne látka
plasticky téct, napětí se v ní nemusí dále zvyšovat. V reálných
plastických látkách může po překročení mezního napětí dojít jak k zvýšení
tak i snížení napětí a přesný popis jejich reologického chování je obtížný.
Přesto, nebo možná právě proto, je v nejpodrobněji vypracované teorii
plasticity, teorii plasticity kovů, StV-model jedním z užívaných modelů
chování látky.
Teorie plasticity kovů je teorie řešící podmínky vzniku a průběhu plastického tečení ve složitých geometrických podmínkách [28], [29], [30]. Základní úlohou je rozšířit podmínku mezního napětí na trojrozměrný případ. Dále je třeba stanovit rychlost plastického toku, která např. podmínkami (2,70) určena není. Přitom pro různé druhy a obory plastického tečení je třeba užívat různé modely plastického chování látek. Teorie plasticity je matematicky náročná a v celé řadě bodů její koncepce nejsou zcela ustálené.
StV-model (obr.35) je základním modelem plastické látky, podobně jako H-model (obr29a) ) a N-model (obr.29b) ) jsou základními modely elastické resp. viskózní látky. Spojením H-a N-modelů jsme získali reologické modely viskoelastických látek, spojením StV-modelů s modely H a N získáme reologické modely dalších druhů látek. Takovým modelům budeme říkat obecné reologické modely a podrobněji se jimi budeme zabývat v následujícím článku. V tomto článku podrobněji probereme ty z reologických modelů, které popisují látky převážně plastického charakteru.
Spojíme-li sériově
StV-model s modelem H,
získáme model, který se nazývá Prandtlův a stručně se označuje jako P-model. Použijeme-li způsob značení
vyložený v předešlém článku, lze složení Prandtlova modelu schematicky
vyjádřit jako P = H - StV. Prandtlův
model
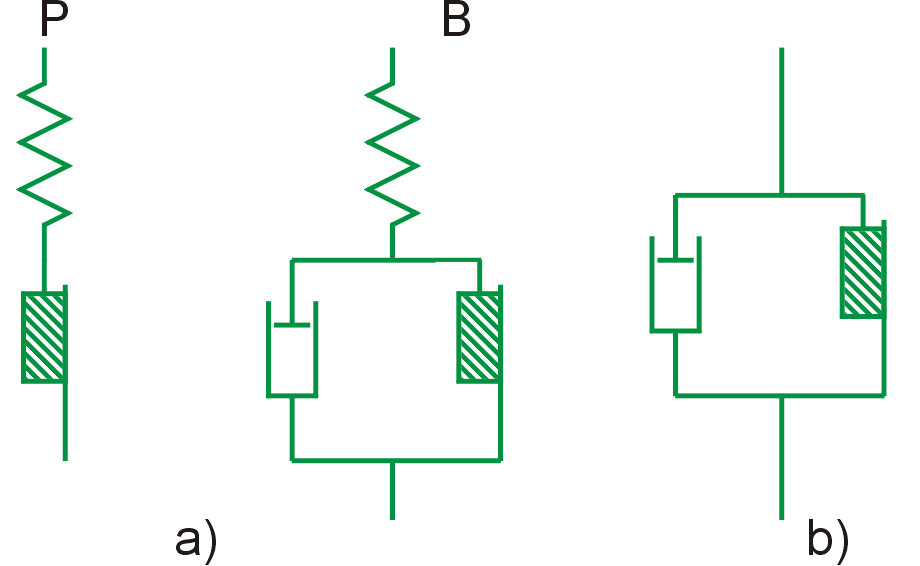
(obr.36a) ) vystihující chování látky, která před vznikem plastického
tečení se elasticky deformuje, bývá užíván pro popis plasticity kovů
v oboru malých plastických deformací. Pro vystižení toku reologicky
složitějších kapalin se užívá model Binghamův (B); B = H - StV/N. Jeho
grafické znázornění je na obr.36b).
Při výpočtech pohybu kapalin bývá někdy (např. [22] ) Hookův člen
pokládán za tuhý (modul
 ) a uvažuje se pouze model StV/N
(viz obr.36c). Takovému modelu
odpovídají reologické rovnice
) a uvažuje se pouze model StV/N
(viz obr.36c). Takovému modelu
odpovídají reologické rovnice

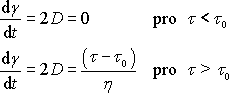 .
(2,71)
.
(2,71)
Chování StV/N
látky je charakterizováno dvěma konstantami, hodnotou mezního
napětí
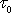 a viskozitou h, která určuje průběh
tečení pro
a viskozitou h, která určuje průběh
tečení pro
 .
.
Na obr.37 je křivkou 1 znázorněna závislost rychlosti
deformace na napětí odpovídající Binghamovu modelu a křivkou 2 závislost reálné
kapaliny, jejíž chování při tečení se blíží chování B-modelu. Kapalinu, jejíž chování je popsáno Binghamovým modelem,
označujeme jako binghamskou nebo též
plastickou kapalinu. Křivka 1 spolu s nulovou hodnotou rychlosti deformace
pro t menší než
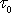 přesně odpovídá rovnicím
(2,71)
, a tedy i
modelu z obr.36c). Závislost
ovšem odpovídá i modelu z obr.36b), protože znázorněna je jen rychlost
deformace a ne deformace samotná (rychlost deformace odpovídající Hookovu členu
záleží na rychlosti změny t, a ta se v grafu z obr.37 neuvažuje).
přesně odpovídá rovnicím
(2,71)
, a tedy i
modelu z obr.36c). Závislost
ovšem odpovídá i modelu z obr.36b), protože znázorněna je jen rychlost
deformace a ne deformace samotná (rychlost deformace odpovídající Hookovu členu
záleží na rychlosti změny t, a ta se v grafu z obr.37 neuvažuje).
Přechod k plastickému tečení látek se projeví i při tahové zkoušce (srov. stať 2.6.1). Výrazná plasticita kovů a některých polymerních látek (hovorové označení plastické hmoty) umožňuje zpracování látek lisováním, kováním, obecně tvářením. Proto se pro plastickou látku užívá i název tvárná látka. Plasticita je důležitá nejen při právě zmíněné výrobě různých součástek, ale i v řadě dalších oborů, např. ve stavebnictví, kde je třeba zkoumat odolnost použitých materiálů a podloží proti plastickému tečení nebo při zkoumání geologického vývoje Země.