LogickĂŠ sĂtÄ rozebranĂŠ v odstavci 7.3 a 7.4. byly pĹĂkladem kombinaÄnĂch logickĂ˝ch systĂŠmĹŻ. VĂ˝stupy tÄchto systĂŠmĹŻ v urÄitĂŠm okamĹžiku zĂĄvisely tedy prĂĄvÄ jen na stavech vstupĹŻ tĂŠto sĂtÄ v tĂŠmĹže okamĹžiku (pĹesnÄji pĹed dobou danou dobou prĹŻchodu elektronickĂ˝mi obvody tvoĹĂcĂmi tuto sĂĹĽ). FunkÄnĂ zĂĄvislost mezi vstupy a vĂ˝stupy byla jednou provĹždy dĂĄna zapojenĂm sĂtÄ a nebylo moĹžnĂŠ tuto zĂĄvislost mÄnit jinak, neĹž zmÄnou zapojenĂ. KombinaÄnĂ logickĂŠ systĂŠmy tedy nemajĂ pamÄĹĽ, tj. nemohou v sobÄ uchovat informaci obsaĹženou ve vstupech sĂtÄ po dobu delĹĄĂ, neĹž je tato informace na vstupech fyzicky pĹĂtomna.
Ĺada logickĂ˝ch sĂtĂ pracuje v synchronismu s posloupnostĂ impulsĹŻ, kterĂŠ jsou generovĂĄny zvlĂĄĹĄtnĂm generĂĄtorem, kterĂ˝ nenĂ souÄĂĄstĂ tĂŠto sĂtÄ. ZmÄna stavu vĂ˝stupu takovĂŠ logickĂŠ sĂtÄ pak zĂĄvisĂ jednak na stavu vstupĹŻ sĂtÄ pĹi pĹĂtomnosti impulsu, jednak mĹŻĹže zĂĄviset na historii vstupĹŻ, tj. na jejich stavech pĹi pĹĂtomnosti dĹĂvÄjĹĄĂch impulsĹŻ. TakovĂ˝mto obvodĹŻm ĹĂkĂĄme sekvenÄnĂ logickĂŠ systĂŠmy a ĹĂdĂcĂ impulsy nazĂ˝vĂĄme hodinovĂ˝mi impulsy. Je zĹejmĂŠ,Ĺže sekvenÄnĂ obvody musĂ obsahovat prvky, kterĂŠ jsou schopny si pamatovat informace minimĂĄlnÄ po dobu mezi dvÄma hodinovĂ˝mi impulsy.
ZĂĄkladnĂm obvodem, kterĂ˝ je
schopen setrvat v urÄitĂŠm stavu (logickĂŠ 0 nebo 1) bez
aplikace vnÄjĹĄĂch logickĂ˝ch ĂşrovnĂ (mimo napĂĄjecĂ
napÄtĂ ovĹĄem) je tzv.pamÄĹĽovĂĄ buĹka, neboli klopnĂ˝ obvod.
NejjednoduĹĄĹĄĂ klopnĂ˝ obvod vytvoĹĂme pomocĂ dvou
invertorĹŻ, kterĂ˝m kĹĂĹžem propojĂme vstupy a vĂ˝stupy (viz
obr. 7.26a). Po zapojenĂ napĂĄjecĂho napÄtĂ nastavĂ se na
vĂ˝stupu jednoho invertoru logickĂĄ jedniÄka a na druhĂŠm vĂ˝stupu logickĂĄ nula. Tento stav je
logicky konzistentnĂ, neboĹĽ je-li napĹ. na vĂ˝stupu Q
invertoru I1 logickĂĄ
jedniÄka, je tato i na vstupu A2 invertoru I2,
kterĂ˝ musĂ mĂt tedy na svĂŠm vĂ˝stupu ![]() nulu. Nula je tedy i na vstupu A1
invertoru I1 ,coĹž
odpovĂdĂĄ stavu na jeho vĂ˝stupu. Chceme-li do pamÄĹĽovĂŠ
buĹky âzapisovatâ, tj. nastavovat vĂ˝stup Q do ĂşrovnÄ 0
nebo 1, musĂme pouĹžĂt mĂsto prostĂ˝ch invertorĹŻ
dvojvstupovĂĄ hradla NAND a propojit je spoleÄnÄ se dvÄma
invertory podle obr. 7.26.b.
nulu. Nula je tedy i na vstupu A1
invertoru I1 ,coĹž
odpovĂdĂĄ stavu na jeho vĂ˝stupu. Chceme-li do pamÄĹĽovĂŠ
buĹky âzapisovatâ, tj. nastavovat vĂ˝stup Q do ĂşrovnÄ 0
nebo 1, musĂme pouĹžĂt mĂsto prostĂ˝ch invertorĹŻ
dvojvstupovĂĄ hradla NAND a propojit je spoleÄnÄ se dvÄma
invertory podle obr. 7.26.b.


LogickĂŠ ĂşrovnÄ pro vstupnĂ
signĂĄly SÂ = 1, R = 0 jsou na obrĂĄzku naznaÄeny.
VÂ sekvenÄnĂm logickĂŠm systĂŠmu je tĹeba, aby se nastavenĂ
nebo nulovånà klopných obvodů dålo v synchronismu s
hodinovĂ˝mi impulsy. To lze zabezpeÄit tak, Ĺže mĂsto
invertorĹŻ na obr. 7.26.b.
pouĹžijeme dvoustupovĂĄ hradla NAND, kterĂĄ otevĂrĂĄme
hodinovĂ˝mi impulsy (viz obr. 7.27.a). Je zĹejmĂŠ, Ĺže je-li
ĂşroveĹ na hodinovĂŠm vstupu log 0 (stav mezi dvÄma impulsy),
nezmÄnĂ klopnĂ˝ obvod svĹŻj stav; pamatuje si jej po dobu mezi
dvÄma hodinovĂ˝mi impulsy.
VĹĄimneme si nynĂ pravdivostnĂ tabulky na obr. 7.27.b. Jsou-li
vstupy R a SÂ uzemnÄny (je-li na nich logickĂĄ nula), pak na
vĂ˝stupech ĹĂdĂcĂch hradel je logickĂĄ jedniÄka nezĂĄvisle
na úrovni hodinovÊho vstupu. Výstupy Q a ![]() zůståvajà proto na úrovni, do
kterĂŠ se dostaly pĹed tĂm, neĹž jsme na oba vstupy R
a S logickou nulu pĹivedli. PĹivedenĂm logickĂŠ nuly na oba
vstupy R i S zablokujeme tedy stav vĂ˝stupĹŻ Q aÂ
zĹŻstĂĄvajĂ proto na Ăşrovni, do
kterĂŠ se dostaly pĹed tĂm, neĹž jsme na oba vstupy R
a S logickou nulu pĹivedli. PĹivedenĂm logickĂŠ nuly na oba
vstupy R i S zablokujeme tedy stav výstupů Q a ![]() , kterÊ jsou
nynà nezåvislÊ na hodinových impulsech.
, kterĂŠ jsou
nynà nezåvislÊ na hodinových impulsech.
V tabulce je to znĂĄzornÄno indexem n pĹĂsluĹĄnĂŠho vĂ˝stupu Äi vstupu. Index n oznaÄuje stav po pĹĂchodu n-tĂŠho hodinovĂŠho impulsu.

| Rn | Sn | Qn+1 |
| 0 | 0 | Qn |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | ? |
tab. 7.27b
PĹedpoklĂĄdejme nynĂ, Ĺže Sn
= 1, Rn = 0. Po
pĹĂchodu hodinovĂŠho impulsu je pak na vĂ˝stupu hradla A3
logickĂĄ 0 a na vĂ˝stupu hradla A4 logickĂĄ jedniÄka. Prostudujeme-li
logickĂŠ ĂşrovnÄ zapojenĂ uvidĂme, Ĺže obvod nastavĂme
do stavu, kdy Q = 1 a ![]() = 0.
Tento stav setrvĂĄvĂĄ do tĂŠ doby, dokud v dobÄ pĹĂchodu
hodinovÊho impulsu je na vstupech S = 1 a R = 0. Ze symetrie
obvodu okamĹžitÄ plyne, Ĺže pro Sn = 0 a Rn
= 1, nastavĂme obvod po
pĹĂchodu hodinovĂŠho impulsu do stavu Q = 0 aÂ
= 0.
Tento stav setrvĂĄvĂĄ do tĂŠ doby, dokud v dobÄ pĹĂchodu
hodinovÊho impulsu je na vstupech S = 1 a R = 0. Ze symetrie
obvodu okamĹžitÄ plyne, Ĺže pro Sn = 0 a Rn
= 1, nastavĂme obvod po
pĹĂchodu hodinovĂŠho impulsu do stavu Q = 0 a ![]() = 1.
= 1.
Je-li Sn = 1 = Rn, nastavà se výstupy
hradel A3 a A4 po pĹĂchodu hodinovĂŠho impulsu do
stavu logickĂŠ nuly. Tento stav by opÄt implikoval, Ĺže oba
vĂ˝stupy hradel A1 a A2 by mÄly bĂ˝t ve stavu logickĂŠ
jedniÄky, coĹž je nesluÄitelnĂŠ se zapojenĂm klopnĂŠho obvodu.
Ve skuteÄnosti se stane to, Ĺže v zĂĄvislosti na tom, kterĂ˝
z vĂ˝stupĹŻ hradel A3 a A4 stoupĂĄ po ukonÄenĂ hodinovĂŠho
impulsu rychleji, nastavĂ se na vĂ˝stupech ![]() a Q buÄ stav Q = 1 nebo Q = 0. Stav
výstupů proto nezåleŞà ani na stavech vstupů ani na úrovni
hodinovĂŠho impulsu, ale na vnitĹnĂch parametrech obvodu; je to
tedy neurÄitĂ˝ stav a v tabulce je znĂĄzornÄn otaznĂkem.
Proto se pĹi buzenĂ tohoto klopnĂŠho obvodu musĂ pamatovat
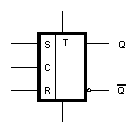
na to, aby stav Rn = Sn = 1 nemohl nastat. Na obr. 7.27.c je
schematickĂĄ znaÄka obvodu.
a Q buÄ stav Q = 1 nebo Q = 0. Stav
výstupů proto nezåleŞà ani na stavech vstupů ani na úrovni
hodinovĂŠho impulsu, ale na vnitĹnĂch parametrech obvodu; je to
tedy neurÄitĂ˝ stav a v tabulce je znĂĄzornÄn otaznĂkem.
Proto se pĹi buzenĂ tohoto klopnĂŠho obvodu musĂ pamatovat
na to, aby stav Rn = Sn = 1 nemohl nastat. Na obr. 7.27.c je
schematickĂĄ znaÄka obvodu.
KromÄ prĂĄvÄ popsanĂŠho
klopnĂŠho obvodu R-S jsou pouĹžĂvĂĄny tĹi dalĹĄĂ typy
klopnĂ˝ch obvodĹŻ: dvojÄinnĂŠ klopnĂŠ obvody J-K, T a D.
DvojÄinnĂŠ klopnĂŠ obvody J-K, D a T odstraĹujĂ neurÄitĂ˝
stav obvodu R-S. Obvod T pracuje jako binĂĄrnĂ obvod, kterĂ˝
mÄnĂ svĹŻj stav po kaĹždĂŠm hodinovĂŠm impulsu Qn+1=
![]() .
.
Pro odstranÄnĂ neurÄitĂŠho stavu klopnĂŠho obvodu R-S byl vyvinut tzv. dvojÄinnĂ˝ klopnĂ˝ obvod J-K. PrincipiĂĄlnĂ zapojenĂ je na obr. 7.28.

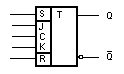
ZapojenĂ obsahuje dva
ĹĂzenĂŠ klopnĂŠ obvody R-S, u nichĹž vĂ˝stupy Q a ![]() prvnĂho jsou navĂĄzĂĄny na vstupy S a
R (po ĹadÄ) druhĂŠho. DruhĂ˝ klopnĂ˝ obvod se ĹĂdĂ
invertovanĂ˝mi hodinovĂ˝mi impulsy a zpÄtnĂĄ vazba je vedena
z vĂ˝stupu druhĂŠho klopnĂŠho obvodu na vstup prvnĂho. PrvnĂ
klopnĂ˝ obvod se nazĂ˝vĂĄ ĹĂdicĂ (master), druhĂ˝ klopnĂ˝
obvod je ĹĂzenĂ˝ (slave). SÂ nĂĄbÄĹžnou hranou hodinovĂŠho
impulsu se nastavuje ĂşroveĹ na vĂ˝stupech ĹĂdĂcĂho obvodu;
ĹĂzenĂ˝ obvod je uzavĹen, neboĹĽ ĂşroveĹ na jeho hodinovĂŠm
vstupu
prvnĂho jsou navĂĄzĂĄny na vstupy S a
R (po ĹadÄ) druhĂŠho. DruhĂ˝ klopnĂ˝ obvod se ĹĂdĂ
invertovanĂ˝mi hodinovĂ˝mi impulsy a zpÄtnĂĄ vazba je vedena
z vĂ˝stupu druhĂŠho klopnĂŠho obvodu na vstup prvnĂho. PrvnĂ
klopnĂ˝ obvod se nazĂ˝vĂĄ ĹĂdicĂ (master), druhĂ˝ klopnĂ˝
obvod je ĹĂzenĂ˝ (slave). SÂ nĂĄbÄĹžnou hranou hodinovĂŠho
impulsu se nastavuje ĂşroveĹ na vĂ˝stupech ĹĂdĂcĂho obvodu;
ĹĂzenĂ˝ obvod je uzavĹen, neboĹĽ ĂşroveĹ na jeho hodinovĂŠm
vstupu ![]() = 0. SÂ ĂşbÄĹžnou
hranou hodinovĂŠho impulsu se uzavĂrĂĄ vstup ĹĂdĂcĂho
klopnĂŠho obvodu a stav na jeho vĂ˝stupu je kopĂrovĂĄn
ĹĂzenĂ˝m klopnĂ˝m obvodem. Jeho vĂ˝stupnĂ ĂşrovnÄ jsou vedeny
zpÄtnou vazbou na vstup ĹĂdĂcĂho obvodu, tam vĹĄak
nezpĹŻsobà Şådnou zmÄnu, neboĹĽ tentokrĂĄt je ĹĂdĂcĂ
obvod uzavĹen (C = 0).
AsynchronnĂ vstupy jsou zavedeny do ĹĂdicĂho klopnĂŠho
obvodu. NastavĂme-li asynchronnĂmi vstupy ĹĂdĂcĂ klopnĂ˝
obvod, pĹesune se tato informace do ĹĂzenĂŠho klopnĂŠho obvodu
okamĹžitÄ (je-li C = 0), neboĹĽ mezi hodinovĂ˝mi impulsy je C =
0, tedy
= 0. SÂ ĂşbÄĹžnou
hranou hodinovĂŠho impulsu se uzavĂrĂĄ vstup ĹĂdĂcĂho
klopnĂŠho obvodu a stav na jeho vĂ˝stupu je kopĂrovĂĄn
ĹĂzenĂ˝m klopnĂ˝m obvodem. Jeho vĂ˝stupnĂ ĂşrovnÄ jsou vedeny
zpÄtnou vazbou na vstup ĹĂdĂcĂho obvodu, tam vĹĄak
nezpĹŻsobà Şådnou zmÄnu, neboĹĽ tentokrĂĄt je ĹĂdĂcĂ
obvod uzavĹen (C = 0).
AsynchronnĂ vstupy jsou zavedeny do ĹĂdicĂho klopnĂŠho
obvodu. NastavĂme-li asynchronnĂmi vstupy ĹĂdĂcĂ klopnĂ˝
obvod, pĹesune se tato informace do ĹĂzenĂŠho klopnĂŠho obvodu
okamĹžitÄ (je-li C = 0), neboĹĽ mezi hodinovĂ˝mi impulsy je C =
0, tedy ![]() = 1; ĹĂzenĂ˝
klopnĂ˝ obvod, ovlĂĄdanĂ˝ signĂĄlem
= 1; ĹĂzenĂ˝
klopnĂ˝ obvod, ovlĂĄdanĂ˝ signĂĄlem ![]() , je tedy otevĹen.
, je tedy otevĹen.
vznikne z obvodu typu J-K,
vloĹžĂme-li invertor mezi vstupy J a K tak, Ĺže K je
komplementem J (obr. 7.29). ZÂ pravdivostnĂ tabulky obvodu J -
K plyne, Şe Qn+1 = 1 pro Dn = Jn = ![]() n = 1
a Qn+1 = 0 pro Dn = Jn =Â
n = 1
a Qn+1 = 0 pro Dn = Jn = ![]() n = 0.
Tedy Qn+1Â =Â Dn. Vzhledem k tomu, Ĺže pravdivostnĂ
tabulka obvodu J-K pro J =
n = 0.
Tedy Qn+1Â =Â Dn. Vzhledem k tomu, Ĺže pravdivostnĂ
tabulka obvodu J-K pro J = ![]() Â se neliĹĄĂ od tabulky obvodu R-S pro
RÂ =Â
 se neliťà od tabulky obvodu R-S pro
RÂ =Â ![]() , mĹŻĹžeme obvod tohoto typu rovnÄĹž
sestavit z ĹĂzenĂŠho obvodu R-S (v tom pĹĂpadÄ hovoĹĂme o
jednoduchĂŠm nebo jednoÄinnĂŠm klopnĂŠm obvodu). TakovĂ˝ obvod
mÄnĂ svĹŻj stav pĹi nĂĄbÄĹžnĂŠ hranÄ hodinovĂŠho impulsu; v
pĹĂpadÄ, Ĺže D obvod sestavĂme z obvodu J-K typu master -
slave, mÄnĂ se stav s tĂ˝lovou hranou hodinovĂŠho impulsu.
KlopnĂŠ obvody typu D mohou slouĹžit jako pamÄti binĂĄrnĂ
informace, kterĂĄ se
vybavĂ hodinovĂ˝m impulsem k dalĹĄĂmu zpracovĂĄnĂ.
PĹĂkladem jednoduchĂŠho obvodu typu D je integrovanĂ˝ obvod
7474 (dva jednoduchÊ D-obvody v jednom pouzdru).
, mĹŻĹžeme obvod tohoto typu rovnÄĹž
sestavit z ĹĂzenĂŠho obvodu R-S (v tom pĹĂpadÄ hovoĹĂme o
jednoduchĂŠm nebo jednoÄinnĂŠm klopnĂŠm obvodu). TakovĂ˝ obvod
mÄnĂ svĹŻj stav pĹi nĂĄbÄĹžnĂŠ hranÄ hodinovĂŠho impulsu; v
pĹĂpadÄ, Ĺže D obvod sestavĂme z obvodu J-K typu master -
slave, mÄnĂ se stav s tĂ˝lovou hranou hodinovĂŠho impulsu.
KlopnĂŠ obvody typu D mohou slouĹžit jako pamÄti binĂĄrnĂ
informace, kterĂĄ se
vybavĂ hodinovĂ˝m impulsem k dalĹĄĂmu zpracovĂĄnĂ.
PĹĂkladem jednoduchĂŠho obvodu typu D je integrovanĂ˝ obvod
7474 (dva jednoduchÊ D-obvody v jednom pouzdru).
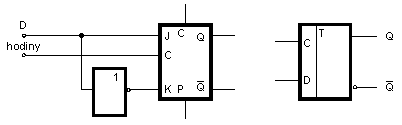
mÄnĂ svĹŻj stav pĹi
kaĹždĂŠm hodinovĂŠm impulsu. Je tedy Qn+1 = ![]() n. ZÂ pravdivostnĂ tabulky obvodu J-K
mĹŻĹžeme vidÄt, Ĺže tuto funkci plnĂ obvod J-K pro JÂ = KÂ = 1.
Obvod typu T mĂĄ tedy dva vstupy - vstup T (spojenĂŠ vstupy J-K)
a vstup pro hodinovÊ impulsy. Je-li T = 1 , obvod se
pĹeklĂĄpĂ, Qn+1 =
n. ZÂ pravdivostnĂ tabulky obvodu J-K
mĹŻĹžeme vidÄt, Ĺže tuto funkci plnĂ obvod J-K pro JÂ = KÂ = 1.
Obvod typu T mĂĄ tedy dva vstupy - vstup T (spojenĂŠ vstupy J-K)
a vstup pro hodinovÊ impulsy. Je-li T = 1 , obvod se
pĹeklĂĄpĂ, Qn+1 = ![]() n, je-li T = 0, obvod zĹŻstĂĄvĂĄ
pĹeklopen do pĹŻvodnĂho stavu; Qn+1 = Qn. Tato funkce obvodu T je vyuĹžita
v synchronnĂoh ÄĂtaÄĂch - viz nĂĹže. Pokud nepotĹebujeme
obvod T elektricky ovlĂĄdat, vystaÄĂme s obvodem typu D ,
u nÄhoĹž spojĂme vĂ˝stup
n, je-li T = 0, obvod zĹŻstĂĄvĂĄ
pĹeklopen do pĹŻvodnĂho stavu; Qn+1 = Qn. Tato funkce obvodu T je vyuĹžita
v synchronnĂoh ÄĂtaÄĂch - viz nĂĹže. Pokud nepotĹebujeme
obvod T elektricky ovlĂĄdat, vystaÄĂme s obvodem typu D ,
u nÄhoĹž spojĂme vĂ˝stup ![]() se vstupem D. Snadno nahlĂŠdneme, Ĺže
je pak Qn+1 =
se vstupem D. Snadno nahlĂŠdneme, Ĺže
je pak Qn+1 = ![]() n.
n.
PĹi aplikacĂch jsou dĹŻleĹžitĂŠ ÄtyĹi typy klopnĂ˝ch obvodĹŻ: klopnĂ˝ obvod R-S (resp. ĹĂzenĂ˝ klopnĂ˝ obvod R-S), klopnĂ˝ obvod J-K, D a T. Obvody typu J-K a D jsou vyrĂĄbÄny v integrovanĂŠ formÄ v rĹŻznĂ˝ch stupnĂch integrace, obvod typu R-S je moĹžnĂŠ sestrojit pomocĂ hradel NAND nebo pouĹžĂt mĂsto nÄj obvod J-K. RovnÄĹž obvod typu T se dĂĄ snadno vytvoĹit z obvodu typu J-K event. z obvodu typu D. KlopnĂŠ obvody mĂvajĂ kromÄ synchronnĂch vstupĹŻ dat jeĹĄtÄ tzv. pĹĂmĂŠ neboli asynchronnĂ vstupy, jimiĹž je moĹžno nastavovat vĂ˝stupy klopnĂŠho obvodu do stavu Q = 1 nebo Q = 0 v dobÄ mezi dvÄma hodinovĂ˝mi impulsy. Je-li klopnĂ˝ obvod typu master-slave, mÄnĂ svĹŻj stav pĹi tĂ˝lovĂŠ hranÄ hodinovĂŠho impulsu; jinak pĹi nĂĄbÄĹžnĂŠ hranÄ. Tabulka 7.4 uvĂĄdĂ pĹehlednÄ pravdivostnĂ tabulky jednotlivĂ˝ch klopnĂ˝ch obvodĹŻ, v dalĹĄĂch odstavcĂch jsou uvedeny jejich nejÄastÄjĹĄĂ aplikace.
Tabulka 7.4
| S-R | J-K | D | T | asynchronnĂ vstupy | |||||||||
| Sn | Rn | Qn+1 | Jn | Kn | Qn+1 | Dn | Qn+1 | Tn | Qn+1 | C | R | S | Q |
| 0 | 0 | Qn | 0 | 0 | Qn | 1 | 1 | 1 | 0 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | Qn | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | * | ||||
| 1 | 1 | ? | 1 | 1 | |||||||||
* viz pravdivostnà tabulky jednotlivých obvodů