---

---

3.1 Fyzikální základy funkce PN přechodu - diodová rovnice

Před nĂĄmi stojĂ­ Ăşkol vysvětlit si na zĂĄkladě minimĂĄlnĂ­ch znalostĂ­ problĂŠm vedenĂ­ elektrickĂŠho proudu v lĂĄtkĂĄch obecně a v polovodičích podrobněji. Tento Ăşkol řeĹĄĂ­ rĹŻznĂ­ autoři rĹŻznĂ˝m zpĹŻsobem, např. (a) odkazem na literaturu, to je pro autora vĂ˝kladu nejjednoduĹĄĹĄĂ­, avĹĄak je-li literatura v dostatečnĂŠ míře nesrozumitelnĂĄ, mĹŻĹže to čtenáře natrvalo odradit od dalĹĄĂ­ho studia problematiky, (b) vysvětlovĂĄnĂ­m pohybu elektronĹŻ a děr v polovodiči pomocĂ­ ”kuliček” a ”bublin” a obdobnĂ˝mi dalĹĄĂ­mi vĂ˝klady typu kuchařskĂŠ knihy. TakovĂ˝ vĂ˝klad poklĂĄdĂĄm za daleko horĹĄĂ­ neĹž odkaz na literaturu, neboĹĽ zatĂ­mco ten čtenáře v principu nemusĂ­ zcela odradit od zĂĄjmu studovat alespoň aplikace elektronickĂ˝ch součástek, vĂ˝klad (b) zpĹŻsobĂ­ chybnĂŠ představy o probĂ­hajĂ­cĂ­ch dějĂ­ch, kterĂ˝ch se Şåk velmi těžko zbavuje. Je moĹžnĂ˝ i přístup (c), kdy se vychĂĄzĂ­ z nebe spadlĂ˝ch nelineĂĄrnĂ­ch charakteristik přísluĹĄnĂ˝ch polovodičovĂ˝ch prvkĹŻ a vĂ˝klad proč jsou takovĂŠ jakĂŠ jsou se ignoruje.

JĂĄ vychĂĄzĂ­m z toho, Ĺže je potřeba vědět alespoň principiĂĄlně o jakĂŠ fyzikĂĄlnĂ­ děje se při vedenĂ­ proudu v pevnĂ˝ch lĂĄtkĂĄch jednĂĄ a pokusĂ­m se proto o vĂ˝klad typu ”KvalifikačnĂ­ příručka pro dělnĂ­ky a mistry”. Bude vychĂĄzet z fyzikĂĄlnĂ­ho popisu chovĂĄnĂ­ elektronĹŻ v lĂĄtkĂĄch pomocĂ­ kvantovĂŠ mechaniky tak, jak ho jiĹž znĂĄte z přednĂĄĹĄek kvantovĂŠ mechaniky a statistiky. Pokud jste si zvolili navĹĄtěvovat moji přednĂĄĹĄku v niŞťích ročnĂ­cĂ­ch a tyto přednĂĄĹĄky jste jeĹĄtě neměli, mĹŻĹžete si vĂ˝klad stejně přečíst a případně po absolvovĂĄnĂ­ uvedenĂ˝ch přednĂĄĹĄek se k němu vrĂĄtit; velice by mne potěšilo, kdyby se vĂĄm podařilo vĂ˝klad pochopit i bez absolvovĂĄnĂ­ těchto přednĂĄĹĄek; to bylo totiĹž mĂ˝m zĂĄměrem. JĂĄ osobně povaĹžuji přínos kvantovĂŠ mechaniky pro vĂ˝klad jevĹŻ spojenĂ˝ch s vedenĂ­m proudu v pevnĂ˝ch lĂĄtkĂĄch za jeden z nejdĹŻleĹžitějĹĄĂ­ch příspěvkĹŻ, kterĂ˝mi kvantovĂĄ mechanika ovlivnila naĹĄe chĂĄpĂĄnĂ­ okolnĂ­ho světa.

3.1.1 PeriodickĂŠ potenciĂĄly a energetickĂŠ pĂĄsy v pevnĂŠ lĂĄtce

Atomy v pevné látce jsou uspořádány v prostorové mřížce, která se periodicky opakuje. Pohybuje-li se elektron jako nosič náboje touto periodickou strukturou, ”vidí” potenciály jednotlivých atomů a pokud se dostane do blízkosti některého z jader, ”pocítí” odpudivou sílu, která mu nedovolí se do blízkosti jádra přiblížit. V oblasti mezi atomy bude elektron pod vlivem přitažlivého coulombického potenciálu, neboť tento potenciál ubývá, jako síla dalekého dosahu, pomalu jako 1/r. Pokud jsou atomy dostatečně blízko sebe, může elektron ”vidět” coulombické potenciály od několika různých jader současně, jinými slovy příspěvky coulombického potenciálu od různých jader se skládají a vytvářejí kombinovaný potenciál, který pak popisuje sílu působící na elektron.

Pro zjednodušení situace si prostorové periodické uspořádání atomů v krystalu látky představujeme jen v jedné souřadnici - jednorozměrně. Musíte mi věřit, že i tento velmi zjednodušená představa vede k velmi solidnímu popisu dějů spojených s vodivostí v pevných látkách. V jednorozměrném přiblížení budou jádra atomů jednoduše rozmístěna periodicky po ose úseček (černé tečky) a na osu pořadnic vynášejme průběh potenciálu. Obr. 3.1.

obr. 3.1.

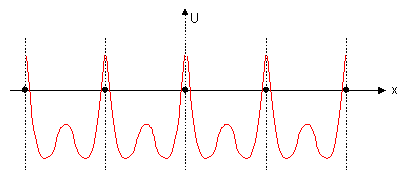
Abychom porozuměli průběhu potenciálu, uvědomme si, že derivace (strmost se znaménkem) potenciálové křivky představuje intenzitu elektrického pole a že tedy síla působící na elektron je přímo úměrná této derivaci (s opačným znaménkem). Strmé části křivek v blízkosti jader představují potenciál odpudivých sil od jádra, které rychle klesají se vzdáleností (síly krátkého dosahu) a v určité vzdálenosti od jádra již existuje jen složený (zde od dvou jader) přitažlivý coulombický potenciál. V osamoceném atomu se elektron pohybuje ”někde” v potenciálovém ”příkopu” vytvořeném složením odpudivého potenciálu jádra a přitažlivého coulombického potenciálu. I když toto bude částečně pravda i v našem případě lineární mřížky, vidíme, že coulombické potenciály od dvou sousedních jader se skládají a vytvářejí ”vlnku” s maximem nižším než nula (coulombický potenciál je v nekonečnu nula a má-li být síla přitažlivá, musí potenciál směrem k jádru klesat do záporných hodnot; teprve v blízkosti jádra vlivem superpozice s potenciálem odpudivých sil vzroste potenciál nad nulu). Pokud je tedy elektron na vyšší energetické hladině, má šanci cestovat periodickou strukturou, jinými slovy přestává být lokalizován ke ”svému jádru”. Bystrá čtenářka již jistě odhalila problém - jak se může pohybovat elektron ve směru osy x od jednoho jádra ke druhému, když mu v cestě stojí odpudivé potenciálové bariéry v blízkosti jader? Odpověď dává tzv. tunelový efekt (řeší se v kvantové mechanice), který umožňuje částici s energií E ”protunelovat” potenciálovou bariéru s amplitudou vyšší než E za předpokladu, že bariéra je ”tenká”. Vzhledem k tomu, že síly odpuzující elektron od jádra jsou síly krátkého dosahu, je přirozené předpokládat, že bariéra tvořená potenciály těchto sil v našem jednorozměrném případě je velmi tenká, a že tedy elektrony mají značnou šanci protunelovat od jednoho jádra ke druhému, tedy být ”delokalizovány”. To však, jak hned ukážeme, ještě neznamená, že mohou vést proud.

obr. 3.2a

obr. 3.2b

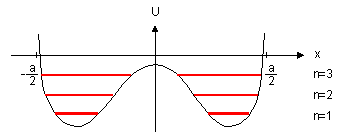
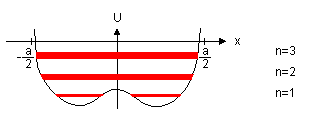
Jsou-li atomy osamocené, nebo dostatečně daleko od sebe, nepůsobí prakticky na sebe, elektrony jsou lokalizovány v blízkosti ”svých” jader a jejich energie jsou diskrétní hladiny, obdobně, jako to pro atom vodíku budete počítat v kvantové mechanice, viz obr. 3.2a. Přibližujeme-li atomy k sobě, ruší se částečně coulombické přitažlivé síly a elektrony přestávají být lokalizovány, viz obr. 3.2b. Tento efekt vzrůstá s dalším přibližováním atomů a stále více a více elektronů přestává být lokalizováno ke svým původním jádrům. Přitom dochází k ”rozmazání” diskrétních energetických hladin na pásy, což je důsledek tzv. Pauliho vylučovacího principu, který říká, že nemohou existovat dva elektrony ve stejném kvantovém stavu. Pokud je atom osamocený, nastává tzv. degenerace energetických hladin, tj. situace, kdy několik elektronů v různých kvantových stavech obsazuje energetickou hladinu o téže energii. Působením vnějšího pole (v našem případě coulombickou interakcí ostatních jader) se degenerace tzv. snímá a energetické hladiny se štěpí na tolik podhladin, aby každému stavu elektronu příslušela (o něco málo) různá energie. Velikost rozštěpení hladin je závislé na intenzitě vnějšího pole a tedy na vzdálenosti atomů od sebe. Můžeme si tedy velmi schematicky tento efekt znázornit tak, jak je uvedeno na obr. 3.3. Na ose x je vzdálenost atomů od sebe v mřížce, na ose y energie. Provedením ”řezu” přes rozštěpené energetické hladiny pro x rovné (lineární) mřížkové konstantě získáme tzv. energetický pásový diagram tak, jak jej budeme pro náš výklad v dalším používat. Vidíme, že energetické pásy (intervaly) energií, které mohou elektrony nabývat (vyšrafované), mohou být odděleny tzv. pásy zakázaných energií, zakázanými pásy.

obr. 3.3

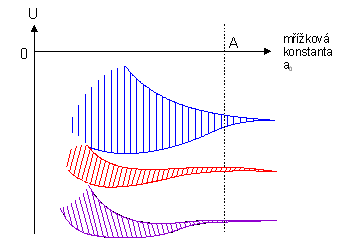
Pro vedení elektrického proudu v pevné látce jsou rozhodující dva pásy. Směrem od nejnižších energií poslední plně obsazený pás a následující zcela prázdný pás. Vysvětleme si nyní, proč tomu tak je. Elektrony jsou částice, které, jak jsme si již řekli, poslouchají Pauliho vylučovací princip. Představme si, že jste Stvořitelem a že tvoříte svůj první atom při teplotě absolutní nuly. Elektrony budou postupně zaplňovat energetické hladiny počínaje od té nejnižší, ale na té nemůže být nekonečný počet částic (to by bylo v případě bosonů, částic s celočíselným spinem), a proto se budou postupně obsazovat i další energetické hladiny až se dostaneme do situace, kdy nám dojdou elektrony. V atomu pak budou za teploty absolutní nuly obsazeny energetické hladiny od té, co odpovídá nejnižší energii až po určitou energii. Hladiny odpovídající energiím vyšším zůstanou prázdné. Obdobně je tomu i v pevné látce, tam se ale postupně zaplňují pásy povolených energií až zaplníme ten nejvyšší a nad ním už další možné pásy zůstanou volné. Může se taky stát, že nejvyšší pás nezaplníme zcela; diskusi tohoto případu si však ponecháme až nakonec, nyní probereme případ, že při teplotě absolutní nuly máme určitý počet pásů dovolených energií úplně zaplněných. Poslednímu zaplněnému pásu budeme říkat valenční pás, dalšímu nad ním vodivostní pás. Mezi valenčním a vodivostním pásem je interval zakázaných energií, tzv. zakázaný pás. Šířka tohoto intervalu zakázaných energií, zkráceně budeme říkat šířka zakázaného pásu je rozhodující pro vodivost látky. Ohřejeme-li nyní látku na pokojovou teplotu, dodáme tím elektronům v látce určitou energii. Obdobně jako je tomu u ideálního plynu, nebudou mít všechny elektrony stejnou energii, ale energie náhodně vybraného elektronu bude popsána tzv. rozdělovací funkcí elektronů podle energie (u molekul ideálního plynu se jedná o tzv. Maxwellovo-Boltzmannovo rozdělení). Tato rozdělovací funkce nám vyjadřuje pravděpodobnost, že náhodně vybraný elektron bude mít energii v předem stanoveném intervalu od E do E+dE. Z toho, jak jsme si popisovali obsazení energetických pásů elektrony za teploty absolutní nuly plyne, že tato funkce má hodnotu rovnou jedničce až do určité energie a nad ní má hodnotu rovnou nule. Tuto energii pod níž při teplotě absolutní nuly jsou všechny povolené energetické hladiny obsazeny, a nad níž jsou všechny povolené energetické hladiny prázdné, nazýváme Fermiho energií. Poznamenejme, že definice rozdělovací funkce je formulována tak, že rozdělovací funkce existuje i pro energie, které jsou v dané látce pro elektrony zakázány; pojem rozdělovací funkce se vztahuje k popisu energií elektronů a nikoliv k dané látce. Pokud bychom měli látku, ve které by žádné intervaly zakázaných energií neexistovaly, tak by obsazení energetických hladin elektrony bylo popsáno stejnou rozdělovací funkcí jako v našem modelu, kde zakázané pásy předpokládáme.

Uvažme, jak se může ”pravoúhlý” charakter našeho rozdělení energií změnit při zahřátí látky. Z názoru plyne (někdy je názor zavádějící, ale nikoliv v tomto případě), že zahřátí látky neovlivní nikterak podstatně elektrony obsazující nejnižší energetické hladiny; aby tyto elektrony mohly ”přijmout” tepelnou energii, musely by mít možnost přejít na vyšší energetickou hladinu, tuto možnost ale nemají, neboť hladiny ”nad nimi” jsou obsazeny. Proto bude energetické rozdělení elektronů zahřátím modifikováno jen málo a bude se jednat v podstatě o zaoblení ”rohů” původně ”pravoúhlého” rozdělení. Určitou představu již tedy máme, a proto teď uvedu vzorec pro energetické rozdělení elektronů, obecněji pro nerozlišitelné částice s poločíselným spinem, tzv. Fermi-Diracovo rozdělení. Je dáno vztahem:

f_FD(E)=(1+exp((E-E_F)/kT))^-1.

Vidíme navíc, že pro energii E=E_F se pravděpodobnost obsazení Fermiho hladiny rovná 1/2. Na obr. 3.4. a,b vidíme průběh Fermi-Diracova rozdělení pro T=0 (obr. 3.4a) a pro T>0 (obr. 3.4b). Z toho intuitivně (což pro nás v tomto případě postačí) plyne, že leží-li Fermiho hladina v oblasti intervalu zakázaných energií mezi plně zaplněným valenčním a úplně prázdným vodivostním pásem, bude ležet za teploty absolutní nuly přesně v polovině zakázaného pásu. Výpočet tuto intuitivní představu potvrzuje.

obr. 3.4a a 3.4b

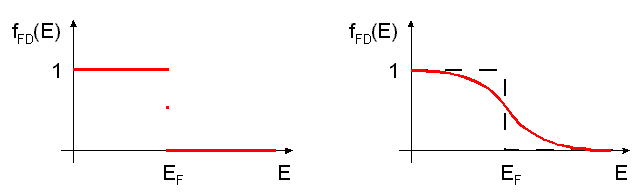
Vraťme se nyní k popisu vodivosti v pevných látkách na základě faktů., která již známe a vysvětleme si nyní, proč jsou valenční a vodivostní pásy tak důležité pro tento popis. Představme si, že látku umístíme do elektrického pole. Elektrický proud je definován jako množství elektrického náboje, které projde plochou průřezu vodiče za jednotku času. Aby došlo k pohybu nosičů náboje v látce je třeba, aby došlo k urychlení elektronů z klidu. Jinými slovy je třeba, aby elektrony získaly od elektrického pole energii. To však není možné, neboť valenční pás je plně obsazen a není v něm tedy jediná volná energetická hladina. Ty jsou až za pásem zakázaných energií, ve vodivostním pásu. Pro odhad vodivosti látky je tedy důležité vědět, zda ve vodivostním pásu jsou nějaké nosiče náboje, příp, odhadnout jejich koncentraci. Při teplotě absolutní nuly víme, že koncentrace elektronů ve vodivostním pásu je nulová. Ohřejeme-li látku na pokojovou teplotu, existují již ”v chvostu”, tj. vysokoenergetické části rozdělovací funkce elektrony, které mají energii potřebnou na překonání zakázaného pásu, jejich koncentrace však ubývá exponencielně se zvětšováním šířky zakázaného pásu, kterou budeme v dalším značit E_g (z anglického gap). Tento fakt plyne z uvedeného vztahu pro Fermi-Diracovo rozdělení pro případ E >> E_F; E_F zanedbáme vůči E a jedničku ve jmenovateli zanedbáme vůči exponenciele a dostáváme přibližný vztah pro naši podmínku vyšších energií f_FD » exp(-E/kT). Tento vztah je (až na normalizační konstantu) totožný s Maxwellovským-Boltzmannovským rozdělením (f_MB(E)) pro ideální plyn, obecněji s klasickým rozdělením pro rozlišitelné částice. Počet elektronů s energií větší než E_g najdeme jednoduše integrací tohoto vztahu od E_g do nekonečna a dostaneme obdobnou exponencielní závislost, jen místo E bude v exponentu E_g (zkuste si to). Počet elektronů, které jsou schopny dostat termickou excitací přes pás zakázaných energií, tedy exponencielně klesá se zvětšující se šířkou zakázaného pásu. Exponenciele exp(-E_g/kT) se někdy říká Boltzmannův faktor (angl. Boltzmann factor). Složitější výpočet s pomocí kvantové mechaniky nám dává pro hustotu elektronů ve vodivostním pásu následující vztah:

n=(1/4)(8pm_e*.k.T/h²)^3/2.exp(-(E_c-E_F)/kT),

kde E_c je poloha (hodnota) spodnĂ­ hranice vodivostnĂ­ho pĂĄsu, m_e* tzv. efektivnĂ­ hmotnost elektronu a h Planckova konstanta. ZnamenĂĄ to, Ĺže pro lĂĄtku se zakĂĄzanĂ˝m pĂĄsem ĹĄirokĂ˝m E_g=1.09 eV (křemĂ­k) (bez příměsĂ­ a v tepelnĂŠ rovnovĂĄze) bude hustota elektronĹŻ ve vodivostnĂ­m pĂĄsu při pokojovĂŠ teplotě (kT=28.7 meV) asi 1,5.10¹⁶ m^-3.

Proč elektrony nemohou zĂ­skat dostatečnou energii k překonĂĄnĂ­ zakĂĄzanĂŠho pĂĄsu z elektrickĂŠho pole? VysvětlenĂ­ tkvĂ­ v Ăşvaze, Ĺže pohybujĂ­cĂ­ se elektron mĹŻĹže zĂ­skĂĄvat energii jen na drĂĄze, kdy neinteraguje s atomy v mříži, tj. na statistickĂŠ střednĂ­ volnĂŠ drĂĄze. Ta je v pevnĂŠ lĂĄtce v řádu 10^-8 m a bylo by třeba pole o intenzitě cca 10⁸ V/m, abychom elektron urychlili na pouhĂ˝ jeden eV (elektronvolt) coĹž je zhruba šířka zakĂĄzanĂŠho pĂĄsu pro křemĂ­k.

tab. 3.1

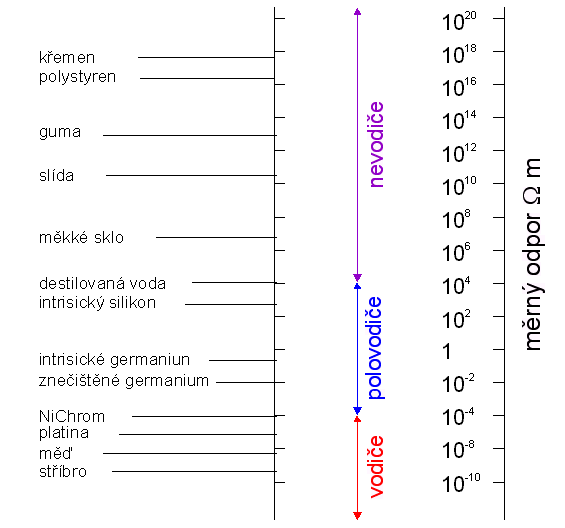
Na zĂĄkladě těchto znalostĂ­ jiĹž mĹŻĹžeme kvalitativně vysvětlit velmi rozdĂ­lnou elektrickou vodivost lĂĄtek tak, jak je uvedena při pokojovĂŠ teplotě v tabulce 3.1. VidĂ­me, Ĺže rozsah měrnĂ˝ch odporĹŻ lĂĄtek zahrnuje hodnoty od cca 10¹⁸ W.m u křemene aĹž do hodnoty cca 10^-9 W.m u stříbra, tedy 27 řádĹŻ. UvědomĂ­me-li si, Ĺže vodivost lĂĄtky je ĂşměrnĂĄ koncentraci volnĂ˝ch nosičů nĂĄboje a fakt, Ĺže tato koncentrace zĂĄvisĂ­ exponenciĂĄlně na šířce zakĂĄzanĂŠho pĂĄsu, je kvalitativnĂ­ vysvětlenĂ­ nasnadě. Změna šířky zakĂĄzanĂŠho pĂĄsu o pouhĂ˝ch 56 meV zpĹŻsobĂ­ e @ 3.7 nĂĄsobnou změnu tĂŠto koncentrace, zvětĹĄenĂ­ šířky zakĂĄzanĂŠho pĂĄsu o 1 eV zpĹŻsobĂ­ zmenĹĄenĂ­ koncentrace nosičů danou faktorem 4.10^-9. Je tedy zřejmĂŠ, Ĺže hlavnĂ­ charakteristickou veličinou, kterĂĄ bude rozdělovat pevnĂŠ lĂĄtky na vodiče, polovodiče a izolanty, bude šířka zakĂĄzanĂŠho pĂĄsu.

Mezi izolanty řadíme látky se šířkou zakázaného pásu od cca 2-3 eV. Typický příklad pásové struktury izolantu vidíme na obr. 3.5., kde jsou, na rozdíl od obr. 3.3., zakresleny též energetické pásy. Ve srovnání s obr. 3.3. je obr. 3.5 nakreslen nikoliv pro hypotetickou substanci, ale pro chlorid draselný, KCl. Zakázaný pás této pevné látky má šířku cca 10 eV,

obr. 3.5

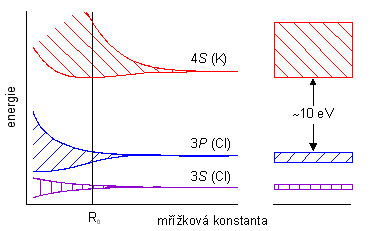
což odpovídá Boltzmannovu faktoru pro pokojovou teplotu v řádu 10^-167 a znamená to, že ve vodivostním pásu chloridu draselného nemůže být za pokojové teploty prakticky žádný nosič náboje; proto je KCl velmi dobrý izolant.

Polovodiče se liší od izolantů pouze šířkou zakázaného pásu. Typickým představitelem a materiálem pro drtivou většinu polovodičových součástek je křemík se šířkou zakázaného pásu 1.09 eV, jehož pásová struktura je znázorněna na obr. 3.6. Příklady dalších polovodičů a šířek jejich zakázaných pásů: germanium (Ge), 0.72 eV, Galium arsenid (GaAs), 1.34 eV,

obr. 3.6

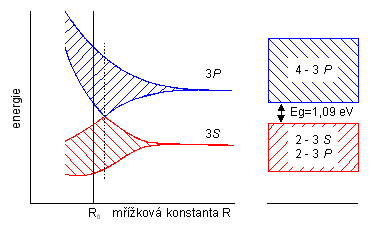
Indium antimonid (InSb), 0.18 eV, sirnĂ­k kademnatĂ˝ (CdS), 2.45 eV, oxid zinečnatĂ˝ (ZnO), 3.3 eV. ZĂĄkladnĂ­ charakteristickĂŠ parametry křemĂ­ku a germania vidĂ­me v tabulce 3.2. K tabulce se vrĂĄtĂ­me později, nynĂ­ si vĹĄimněme pouze počtu atomĹŻ na m³ a tzv. vlastnĂ­ (intrinsickĂŠ) koncentrace nosičů nĂĄboje. Počet atomĹŻ na m³ se u obou polovodičů příliĹĄ neliĹĄĂ­, ale vlastnĂ­ koncentrace nosičů nĂĄboje se liĹĄĂ­ cca o 3 řády. To je dĂĄno zejmĂŠna rozdĂ­lem v šířce zakĂĄzanĂŠho pĂĄsu, kterĂ˝ činĂ­ 0.37 eV.

U kovů neexistuje zakázaný pás mezi vodivostním a valenčním pásem, tyto dva pásy tvoří vlastně jeden ne zcela zaplněný pás. Na obr. 3.7. vidíme pásový diagram pro měď jako typický příklad kovu s dobrou elektrickou vodivostí.

obr. 3.7

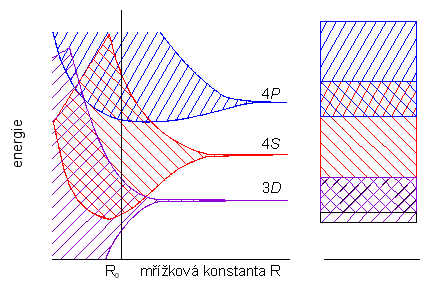
Pro vodiče v pevné fázi (kovy) tedy platí, že nemají zakázaný pás; proto jejich elektrony, je-li vodič vložen do elektrického pole, mohou být tímto polem urychleny, neboť existuje množství volných vyšších energetických hladin, na které mohou elektrony (se zachováním Pauliho principu) přejít. Proč tedy existují rozdíly mezi vodivostí jednotlivých kovů? Odpověď nám dá bližší pohled na přenos náboje v elektrickém poli, který je vysvětlen v následujícím odstavci.

3.1.2 Elektronová a děrová vodivost pevných látek

V tomto odstavci budeme předpoklĂĄdat, Ĺže ve vodivostnĂ­m pĂĄsu polovodiče, eventuelně v překrĂ˝vajĂ­cĂ­ch se pĂĄsech kovu je dostatečnĂĄ koncentrace volnĂ˝ch elektronĹŻ a budeme studovat, co se s nimi děje nenĂ­-li na lĂĄtku přiloĹženĂŠ elektrickĂŠ pole a dĂĄle s přiloĹženĂ˝m elektrickĂ˝m polem. Nejprve prvnĂ­ případ. SpočítĂĄme-li nejpravděpodobnějĹĄĂ­ rychlost elektronu z MaxwellovskĂŠho rozdělenĂ­ energiĂ­ pro pokojovou teplotu (zde si, jak jiĹž vĂ­me, mĹŻĹžeme dovolit nahradit přesnĂ˝ popis danĂ˝ Fermi-DiracovskĂ˝m rozdělenĂ­m, Maxwell-BoltzmannovskĂ˝m rozdělenĂ­m) podle znĂĄmĂŠho vztahu v_p= (8 kT/pm)^1/2, dostaneme hodnotu v řádu 10⁵ m/s. Jak to, Ĺže lĂĄtkou neteče elektrickĂ˝ proud, kdyĹž je rychlost elektronĹŻ tak vysokĂĄ? Odpověď dĂĄvĂĄ studium pohybu elektronu v lĂĄtce. Spočítanou rychlostĂ­ se elektron nepohybuje dlouhou dobu, neboĹĽ za střednĂ­ volnou drĂĄhu cca 10^-8 m interaguje s ”rĹŻznĂ˝mi objekty” v krystalickĂŠ mříži, jako jsou atomy, fotony, fonony a ostatnĂ­ elektrony. To mĂĄ za nĂĄsledek, Ĺže směr jeho drĂĄhy se změnĂ­. Elektron se tedy pohybuje zcela nĂĄhodnĂ˝mi směry, viz obr.3.8.

obr. 3.8

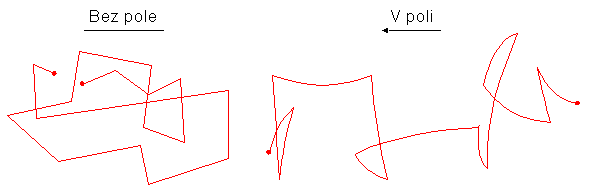
DĂ­vĂĄme-li se na celkovĂ˝ střednĂ­ elektrickĂ˝ proud proteklĂ˝ určitĂ˝m makroskopickĂ˝m průřezem vodiče za ”rozumně dlouhou” dobu, je nutně tento střednĂ­ proud roven nule. KdyĹž vĹĄak připojĂ­me vodič k citlivĂŠmu přístroji, na kterĂŠm mĂĄme moĹžnost sledovat i rychlĂŠ změny napětĂ­ (osciloskop), uvidĂ­me, Ĺže na koncĂ­ch vodiče existuje malĂŠ střídavĂŠ napětĂ­, jehoĹž efektivnĂ­ hodnota roste Ăşměrně s teplotou, odporem vodiče a šířkou frekvenčnĂ­ho pĂĄsma přístroje D f, kterĂ˝m toto napětĂ­ sledujeme, u_ef²=4k.T.R.D f. (Zde k je Boltzmannova konstanta.) Toto napětĂ­, zpĹŻsobenĂŠ prĂĄvě tepelnĂ˝m pohybem elektronĹŻ nazĂ˝vĂĄme thermĂĄlnĂ­, nebo NyquistĹŻv ĹĄum a pro naĹĄe Ăşvahy nenĂ­ zatĂ­m podstatnĂŠ.

Umístíme-li látku do elektrického pole, elektron zachovává svůj tepelný pohyb, ale jeho střední rychlost již není rovna nule, ale směřuje ve směru přiloženého elektrického pole. Této střední rychlosti se říká driftová rychlost a fyzikálnímu efektu drift elektronů v elektrickém poli. Driftová rychlost elektronů je definována vztahem

v_dn=m_n.E,

kde veličině m_n říkáme pohyblivost elektronů. Pokud je driftová rychlost malá ve srovnání s tepelnou rychlostí, je úměrná přiloženému poli E a platí Ohmův zákon v diferenciálním tvaru

i=s_n.E,

kde i je proudová hustota (proud na jednotku plochy průřezu vodiče) a m_n je tzv. (elektronová) vodivost látky (nebudeme stále opakovat, že se jedná o elektrickou vodivost, tepelnou vodivostí se v tomto učebním textu nebudeme zabývat). Je-li v látce koncentrace volných elektronů n a ty se pohybují driftovou rychlostí v_dn, projde za jednotkou času jednotkou plochy průřezu vodiče náboj

e.n.v_dn=e.n.m_n.E,

z čehož plyne pro vodivost

s_n=e.n.m_n

(e je náboj elektronu). Zde vidíme odpověď na otázku položenou v konci předchozího odstavce. Díky různé krystalové struktuře vodiče se liší pohyblivost elektronů ve vodiči a tím se liší i vodivost různých vodivých materiálů. Vidíme, že v kovech je vodivost dána výhradně pohybem elektronů jako nosičů nábojen a proto tuto vodivost nazýváme elektronovou vodivostí.

Vodivost izolantů je zanedbatelně malá a proto má smysl probrat nyní jak to vypadá s vodivostí materiálů, u kterých existuje zakázaný pás mezi valenčním a vodivostním pásem, ale jeho šířka není příliš veliká. Znamená to, že vlivem termické excitace existuje určitá koncentrace elektronů ve vodivostním pásu látky a tyto elektrony přispívají k vedení proudu stejným způsobem jak bylo právě popsáno u vodičů. Na rozdíl od vodičů musíme nyní analyzovat ještě situaci ve valenčním pásu. Při teplotě absolutní nuly je tento pás plně obsazen a nejsou zde tedy volné energetické hladiny. Při teplotě vyšší než absolutní nula jsou některé elektrony excitovány do vodivostního pásu. Je zřejmé, že to budou elektrony obsazující energetické hladiny nejblíže horní hranici valenčního pásu, tj. ty nejvyšší energetické hladiny, neboť pravděpodobnost, že budou excitovány elektrony obsazující nižší energetické hladiny ubývá exponenciálně se ”vzdáleností” (tj. energetickou odlehlostí) příslušné hladiny od horní hranice valenčního pásu. Ve valenčním pásu jsou tedy při, pro jednoduchost pokojové, teplotě volné nejvýše položené energetické hladiny a je jich tam stejné množství (stejná koncentrace), jako elektronů ve vodivostním pásu. Při umístění látky do elektrického pole dojde k postupnému obsazování těchto hladin elektrony, které jsou polem urychlovány, aniž ovšem tyto elektrony byly excitovány do vodivostního pásu. To má za následek, kvalitativně řečeno, efektivní pohyb volných energetických hladin ve směru opačném, než je směr elektrického pole. V látce, kde existuje zakázaný pás o nenulové šířce, existuje rovněž ještě další mechanismus přenosu náboje, a sice ve valenčním pásu. Je úmluvou stanoveno (a vychází to také z kvantově-mechanického modelu), že tento mechanismus se popisuje pohybem nosičů s nábojem opačné polarity, tzv. děr (angl. holes). U látky, kde existuje zakázaný pás o nenulové šířce, je tedy celková vodivost daná součtem dvou příspěvků, elektronové vodivosti způsobené pohybem elektronů ve vodivostním pásu, a děrové vodivosti způsobené pohybem děr ve valenčním pásu,

s = s_n+ s_p.

Děrová vodivost s_p je dána obdobným vztahem jako elektronová vodivost, tj.

s_p= e.p.m_p,

kde p je koncentrace děr ve valenčním pásu, v doposud diskutovaném případě rovná koncentraci elektronů ve vodivostním pásu, p = n. Jak uvidíme za chvíli, tento vztah přestává platit, je-li do čistého, tzv. vlastního (intrinsického) polovodiče přimíchána určitá příměs. Dá se ukázat, že pro koncentraci děr ve valenčním pásu platí obdobný vztah jako pro koncentraci elektronů ve vodivostním pásu a sice

p=(1/4)(8pm_p*.k.T/h²)^3/2.T^3/2exp(-(E_F-E_v)/kT),

kde E_v je hodnota energie odpovídající horní hranici valenčního pásu, m_p* tzv. efektivní hmotnost díry. Je zvykem označovat veličinu n = p = n_i jako tzv. vlastní (intrinsickou) koncentraci nosičů náboje. Porovnáme-li vztahy pro n a p vidíme, že součin

n_i²=n.p=2.((m_e*m_p*).p.kT/h²)³exp(-E_g/kT)

nezávisí na poloze Fermiho hladiny, ale jenom na šířce zakázaného pásu. Dá se ukázat, že tento součin nezávisí ani na koncentraci příměsí a že je to tedy veličina charakterizující materiál a závisící jen na teplotě. Pro zajímavost můžeme s použitím vztahů pro n a p vypočítat polohu Fermiho meze ve vlastním polovodiči; ze vztahu n = p plyne

m_e*^3/2exp(-(E_c-E_F)/kT)=m_p*^3/2exp(-(E_F-E_v)/kT).

Logaritmováním a řešením pro E_F dostáváme

E_F=(1/2)(E_v+E_c)+(3/4)kTln(m_e*/m_p*).

Pro teplotu absolutní nuly leží, jak bylo výše uvedeno Fermiho hladina přesně uprostřed zakázaného pásu, pro vyšší teploty je obecně na teplotě závislá, neboť obecně m_e* je různé od m_p*.

3.1.3 Příměsové polovodiče

Význam polovodičů, zejména křemíku, pro výrobu polovodičových součástek vynikne až popisem tzv. příměsových polovodičů, tj. polovodičů, do kterých byla přidána určitá koncentrace příměsí. Vzhledem k tomu, že křemík je čtyřmocný prvek, používají se příměsi třímocné a pětimocné. Kvalitativní popis funkce příměsí v křemíku je následující.

UmĂ­stĂ­me-li do krystalovĂŠ mřížky křemĂ­ku pětimocnĂ˝ prvek, bude pĂĄtĂ˝ valenčnĂ­ elektron příměsi daleko slaběji vĂĄzĂĄn a bude tedy mĂ­t velkou pravděpodobnost delokalizace, tj. odtrĹženĂ­ od mateřskĂŠho atomu, a bude pak přispĂ­vat k vedenĂ­ proudu. Na mĂ­stě pĹŻvodnĂ­ho atomu příměsi pak zbyde kladnĂ˝, jednou nabitĂ˝, iont. Prakticky kaĹždĂ˝ atom příměsi tak přispěje k celkovĂŠ koncentraci volnĂ˝ch nosičů jednĂ­m elektronem a protoĹže vlastnĂ­ koncentrace nosičů v křemĂ­ku je velmi malĂĄ (zhruba na kaĹždĂ˝ch 5.10¹² atomĹŻ jedinĂ˝ volnĂ˝ elektron a dĂ­ra) stačí velice malĂĄ koncentrace příměsĂ­ k tomu, aby podstatně zvýťila koncentraci elektronĹŻ (nikoliv děr). Např. koncentrace příměsĂ­ 1 ppm, tj. 10^-6, zvýťí koncentraci elektronĹŻ na cca 5.10²² m^-3, tedy o 6 řádĹŻ. Příměsi v tomto případě nazĂ˝vĂĄme příměsi typu n nebo donory, neboĹĽ odevzdĂĄvajĂ­ elektron. Elektrony, jejichĹž koncentrace vzrostla, nazĂ˝vĂĄme majoritnĂ­mi nosiči, dĂ­ry minoritnĂ­mi nosiči. Takto dotovanĂŠmu (termĂ­n pro polovodič obohacenĂ˝ příměsemi) polovodiči říkĂĄme polovodič typu n.

Bude-li v krystalové mříži třímocný atom, bude mít značnou schopnost vázat na sebe jeden elektron (jak uvidíme z pásového diagramu, elektron z valenčního pásu) a tím uvolnit jednu díru ve valenčním pásu. Na místě atomu příměsi pak bude vázaný záporný iont (opět jednou nabitý) příměsi. Opět stačí velmi malá koncentrace příměsi k tomu, aby postatně ovlivnila koncentraci nosičů, tentokrát děr. Příměsi v tomto případě nazýváme příměsi typu p nebo akceptory, neboť přijímají jeden elektron, díry, jejichž koncentrace vzrostla, majoriními nosiči, elektrony minoritními nosiči. Takto dotovanému polovodiči říkáme polovodič typu p.

Dá se ukázat, že v obou případech zůstává součin n.p konstantní, nezávislý na koncentraci příměsí, tj. kolikrát zvýšíme koncentraci elektronů tolikrát snížíme koncentraci děr v případě pětimocné příměsi a v případě třímocné příměsi můžeme formulovat duální obdobu tohoto výroku. Bystrou čtenářku jistě nyní napadne otázka (není vyloučeno, že tato otázka napadne i bystrého čtenáře), proč je tomu tak, že se zvýšením koncentrace nosičů jednoho druhu snížíme koncentraci nosičů druhého druhu? A bystrou čtenářku vzápětí napadne další otázka: jak to, že když termální excitace elektronů stále ”zásobuje” vodivostní pás elektrony, že nedojde k jeho ”přeplnění”? Odpověď na obě otázky je ve fyzikálním efektu, který jsme dosud nezmínili, a tím je tzv. rekombinace. Existuje-li elektron ve vyšším energetickém stavu ve vodivostním pásu, může se snadno stát, že např. při srážce s atomem v mřížce dojde k předání takové energie, že elektron ”spadne” z vodivostního do valenčního pásu, čímž zároveň ”zlikviduje” jednu díru. Hovoříme o rekombinaci páru elektron-díra. Je zřejmé, že pravděpodobnost rekombinace roste s koncentrací buď jednoho nebo druhého nebo obou druhů nosičů a naopak. Je tedy zřejmé, že v případě příměsových polovodičů, kdy koncentrace majoritních nosičů je podstatně větší než koncentrace minoritních nosičů, bude z hlediska rekombinace hrát rozhodující roli koncentrace minoritních nosičů, neboť jak již bylo uvedeno, rekombinace probíhá v párech a není-li druhého do páru, nemůže rekombinace proběhnout. Teď je již jistě, alespoň kvalitativně jasné, proč klesne koncentrace děr při zvýšení koncentrace elektronů a proč se dosáhne rovnovážné koncentrace elektronů ve vodivostním pásu přestože termická generace probíhá neustále; je to dáno procesem rekombinace, který je závislý na koncentraci nosičů obojího druhu.

Abychom si poněkud přesněji popsali proces rekombinace uvažujme polovodič typu n, který po krátkou dobu ozáříme světlem vhodné vlnové délky tak, aby energie fotonů stačila na excitaci elektronů do vodivostního pásu (hovoříme o tzv. vnitřním fotoefektu, elektronické prvky na něm založené probereme později). Budeme sledovat, co se bude dít s koncentrací děr v závislosti na čase. Obecně můžeme napsat rovnici dp/dt=g-r, kde g je rychlost generace a r rychlost rekombinace. Bývá zvykem rychlost rekombinace vyjadřovat pomocí tzv. doby života t_p tak, že poměr dt/t_p vyjadřuje pravděpodobnost rekombinace díry za čas dt. Rychlost rekombinace bude pak dána poměrem r = p/t_p za předpokladu, že máme dostatek elektronů se kterými mohou díry rekombinovat, tj. za předpokladu p«n, což je v příměsovém polovodiči prakticky vždycky splněno. Pro časový průběh koncentrace děr pak máme dp/dt=g-p/t_p. Je-li bez ozáření koncentrace děr p_o a rychlost generace g_o=p_o/t_p, dostáváme pro průběh koncentrace děr při zapnutí záření v čase t=0 (diferenciální rovnice je obdobná rovnici nabíjení kondenzátoru přes odpor; vzpomeňte si na přednášku z elektřiny a magnetismu)

Dp=p-p_o=(g-g_o)t_p(1-exp(-t/t_p)),

neboli, že koncentrace děr narůstá s časovou konstantou t_p z hodnoty p_o na hodnotu p. Po vypnutí záření bychom dostali obdobnou závislost pro relaxaci koncentrace p na původní hodnotu p_o,

Dp=(Dp)_oexp(-t/t_p).

V polovodičích jsou hodnoty t_p v řádu 10^-6-10^-8 s. Tato situace je znázorněna na obr. 3.9a,b.

Obr. 3.9a,b

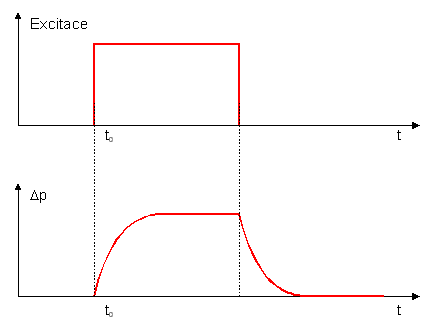
Vzájemná rekombinace elektronů a děr má ještě jeden, pro technologii výroby polovodičových prvků naprosto rozhodující výsledek: Dotujeme-li příměsový polovodič příměsemi opačné vodivosti, zvyšujeme pravděpodobnost rekombinace tím, že zvyšujeme koncentraci nosičů opačné polarity (úvaha v předchozím odstavci pak neplatí, neboť neplatí předpoklad velikého rozdílu koncentrací p a n). Dříve nebo později tedy musíme dospět do situace, že koncentrace původně majoritních nosičů bude stejně velká jako vlastní koncentrace a tedy polovodič bude mít vlastnosti charakteristické pro vlastní, intrinsický polovodič. Pokračujeme-li v dotaci, změníme postupně polovodič jedné vodivosti na polovodič opačného typu vodivosti.

Při popisu příměsových polovodičů pomocí pásových diagramů je výhodné zavést pojem tzv. příměsových hladin, tj. energetických úrovní odpovídajících hladinám příměsí. Jestliže např. je zapotřebí energie E_d’ k tomu, abychom ”utrhli” elektron od atomu příměsi (tato energie je daná jen kombinací polovodič-příměs), pak tzv. donorová hladina bude ležet o E_d’ pod spodní hranicí vodivostního pásu a podobně potřebujeme-li dodat energii E_p’, abychom ”nalepili” elektron na akceptorový atom (tj. vytvořili díru ve valenčním pásu), bude tzv. akceptorová hladina ležet o E_p’ nad horní hranicí valenčního pásu. V dalším budeme uvažovat polovodič s koncentrací donorů N_d a koncentrací akceptorů N_a tak, že např. se bude jednat o polovodič typu n, tj. N_d » N_a. Energie E_d’ a E_a’ jsou pro křemík řádu 50 meV, tedy velmi srovnatelné s tepelnou energií elektronů při pokojové teplotě (cca 28 meV). Většina donorů i akceptorů bude pak tepelně ionizována, budou však existovat neionizované (neutrální) zbytky, jejichž koncentraci označíme po řadě N_dn a N_an. Podle zákona zachování náboje musí celkový náboj v látce zůstat nulový, tedy i v jednotce objemu, tj.

p + (N_d - N_dn) = n + (N_a - N_an),

přičemž z našeho původního předpokladu, že se jedná o polovodič typu n plyne, že N_d - N_dn » N_a-N_an a n » p. Tedy n » N_d - N_dn. Vypočítejme si nyní polohu Fermiho meze v příměsovém polovodiči. Začneme tím, že si určíme koncentraci neionizovaných donorů z Fermi-Diracovy rozdělovací funkce. Pravděpodobnost, že donory zůstanou neionizovány je rovna pravděpodobnosti, že donorová hladina E_d=E_c-E_d’ bude obsazena elektronem a tedy

N_dn=N_d.P_FD(E_d).

ObsazenĂ­ energetickĂŠ hladiny s energiĂ­ E_d je dĂĄno Fermi-Diracovou funkcĂ­ bez integrace, neboĹĽ se jednĂĄ o jednu hladinu (nikoliv energetickĂ˝ interval).

n/N_d=1-N_dn/N_d = 1-(1+exp(E_d-E_F)/kT)^-1.

Pro nízké teploty je zřejmě koncentrace n ve vodivostním pásu téměř nula a to je možné jedině tehdy, když exponentu zanedbáme vůči 1, tj. když E_F>E_d. Pak můžeme předpokládat, že E_F-E_d » kT a tedy, že exponent exponenciály je velký a záporný. Zlomek rozvedeme podle vzorce (1+a)^-1 » 1-a, pokud a « 1. Dostaneme (po zrušení jedniček)

n   N_dexp(-(E_d-E_F)/kT).

Tutéž koncentraci n bychom měli dostat ze vztahu (již uvedeného)

n=(1/4)(8pm_e*.k.T/h²)^3/2.exp(-(E_c-E_F)/kT)=N_c.exp(-(E_c-E_F)/kT),

kde jsme si označili N_c=(1/4)(8pm_e*.k.T/h²)^3/2. LogaritmovĂĄnĂ­m rovnice

N_dexp(-(E_d-E_F)/kT)=N_c.exp(-(E_c-E_F)/kT)

doståvåme kT.ln(N_d/N_c) = 2E_F - E_c - E_d a z toho pro

E_F=(1/2)(E_c+E_d)+(1/2)kT.ln(N_d/N_c).

Veličina N_c (fyzikĂĄlně je to efektivnĂ­ hustota moĹžnĂ˝ch stavĹŻ elektronu ve vodivostnĂ­m pĂĄsu) mĂĄ hodnotu pro křemĂ­k a 300K 3,5.10²⁵ m^-3, je tedy (pro rozumnĂŠ koncentrace příměsĂ­, křemĂ­k mĂĄ cca 5.10²⁸ atomĹŻ na m³) větĹĄĂ­ neĹž N_d a argument logaritmu je menĹĄĂ­ neĹž jedna; z toho plyne, Ĺže pro zvyĹĄujĂ­cĂ­ se teplotu hodnota E_F klesĂĄ. Při nĂ­zkĂ˝ch teplotĂĄch leŞí tedy Fermiho hladina uprostřed mezi donorovou hladinou a spodnĂ­ hranicĂ­ vodivostnĂ­ho pĂĄsu, při zvyĹĄovĂĄnĂ­ teploty klesĂĄ směrem ke středu zakĂĄzanĂŠho pĂĄsu, kam by se přiblĂ­Ĺžila při nekonečně vysokĂŠ teplotě. Pro pokojovĂŠ teploty mĹŻĹžeme předpoklĂĄdat, Ĺže Fermiho hladina (opět pro rozumnĂŠ koncentrace příměsĂ­) je někde mezi středem zakĂĄzanĂŠho pĂĄsu a donorovou hladinou. Je dobrĂŠ si vĹĄimnout, Ĺže při extrĂŠmně vysokĂ˝ch koncentracĂ­ch příměsĂ­ je zĂĄvislost Fermiho energie na teplotě rostoucĂ­ a je tedy moĹžnĂŠ, aby při pokojovĂŠ teplotě leĹžela Fermiho hladina v tomto případě nad spodnĂ­ hranicĂ­ vodivostnĂ­ho pĂĄsu (viz nĂ­Ĺže diskusi o tunelovĂŠ diodě). TakovĂŠmu polovodiči říkĂĄme degenerovanĂ˝, neboĹĽ vykazuje z hlediska vodivosti vlastnosti kovu.

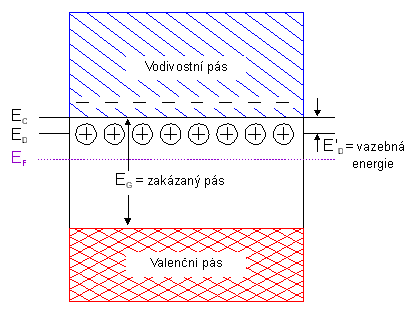
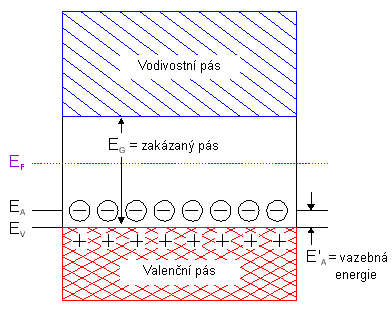
Naprosto stejnou úvahu a výpočet můžeme provést pro dotaci příměsemi typu p. V polovodiči nepříliš dotovaném příměsemi typu p bude tedy Fermiho hladina ležet mezi středem zakázaného pásu a akceptorovou hladinou. Pásové diagramy pro oba případy vidíme na obr.3.10 pro polovodič typu n a na obr. 3.11 pro polovodič typu p.

obr. 3.10

obr. 3.11

3.1.4 PN přechod

Předpokládejme, že se nám podařilo nějakým způsobem vytvořit přechod PN, tj. rozdělit vzorek křemíku myšlenou rovinou. V jedné polorovině materiál dotujeme příměsemi typu n a ve druhé příměsemi typu p. V předchozím odstavci již bylo popsáno, že reálná technologie výroby přechodu PN je založena na faktu, že polovodič jednoho typu vodivosti lze ”předopovat” na opačný typ vodivosti. Skutečný PN přechod se tedy vyrábí tak, že se polovodič jednoho typu vodivosti obohatí v určitém objemu příměsemi opačného typu vodivosti; rozhraní tohoto objemu a původního objemu pak tvoří PN přechod. Obohacení příměsemi se děje nejčastěji buď termickou difuzí, kdy do polovodiče ohřátého na vysokou teplotu difundují skrze povrch polovodiče příměsi z atmosféry, která polovodič obklopuje, nebo tzv. iontovou implantací. Při iontové implantaci se atomy příměsí v plynném stavu ionizují, urychlují a fokusují do svazku s průměrem menším než mikron. Svazek dopadá na povrch polovodiče a proniká do hloubky, určené energií iontů. Při průchodu iontu materiálem dochází k jeho zachycení na určité pozici v krystalové mřížce a zároveň k jeho neutralizaci. Výhoda termické difuze je v relativně jednoduché technologii, výhoda iontové implantace ve velmi přesném vymezení obohacené oblasti.

Pro jednoduchost zkoumejme nyní jednorozměrný model. V tomto modelu předpokládáme tzv. náhlý přechod (abrupt junction), tj. do určité souřadnice x_o je materiál typu p a od téhož x_o je materiál typu n. Na obrázku 3.12 je tato situace zachycena pro x_o=0.

obr. 3.12

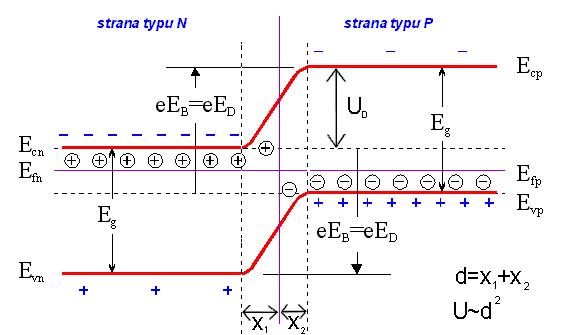
Na ose Ăşseček je tedy vynesen jeden rozměr naĹĄeho modelu, na ose pořadnic je vynesena energie. Z definice Fermiho energie plyne, Ĺže pokud je krystal materiĂĄlu v rovnovĂĄze, existuje jen jedna hodnota energie, nad kterou jsou při teplotě absolutnĂ­ nuly vĹĄechny energetickĂŠ hladiny prĂĄzdnĂŠ a pod kterou za stejnĂŠ podmĂ­nky plně obsazenĂŠ. V naĹĄem modelu bude tedy hodnota E_F nezĂĄvislĂĄ na x, pokud bude krystal v rovnovĂĄze. KdyĹž ale přiloŞíme vnějĹĄĂ­ napětĂ­ nebo přechod ozáříme fotony o vhodnĂŠ vlnovĂŠ dĂŠlce, poruĹĄĂ­me rovnovĂĄhu a vĂ˝slekem pak bude schodovitĂĄ změna Fermiho hladiny pro x=0. ZabĂ˝vejme se vĹĄak nejprve rovnovĂĄĹžnĂ˝m případem a diskutujme, co se stane, kdyĹž přechod PN vytvoříme. Vysvětleme si nejprve poněkud přesněji pojem difuze. Ze zĂĄkladnĂ­ přednĂĄĹĄky MolekulovĂĄ fyzika, z vlastnĂ­ zkuĹĄenosti i ze středoĹĄkolskĂ˝ch znalostĂ­ vĂ­me, Ĺže v plynu nastĂĄvĂĄ usměrněnĂ˝ pohyb částic (molekul, atomĹŻ), je-li v některĂŠm mĂ­stě vyĹĄĹĄĂ­ koncentrace neĹž v jinĂŠm mĂ­stě. Otevřeme-li např. v jednom rohu uzavřenĂŠ mĂ­stnosti voňavku, za chvĂ­li ji ucĂ­tĂ­me i ve druhĂŠm rohu mĂ­stnosti (a to i v případě, Ĺže v mĂ­stnosti vzduch neproudĂ­). Tomuto jevu říkĂĄme difuze, je zpĹŻsobena tepelnĂ˝m pohybem částic a v jednorozměrnĂŠm přiblĂ­ĹženĂ­ ji mĹŻĹžeme popsat jednoduchou rovnicĂ­ Q = -D.dn/dx, kde Q je počet částic proĹĄlĂ˝ch jednotkovou plochou za jednotku času (proudovĂĄ hustota, rozměr m^-2s^-1), D je difuznĂ­ koeficient (s rozměrem m²s^-1), n je koncentrace částic a x je rozměr, podĂŠl něhoĹž difuzi studujeme. VidĂ­me, Ĺže Q je ĂşměrnĂŠ gradientu koncentrace; zĂĄpornĂŠ znamĂŠnko nĂĄm říkĂĄ, Ĺže proud částic směřuje proti směru vzrĹŻstu koncentrace. Efekt difuze nenĂ­ nikterak omezen na plynnĂĄ prostředĂ­ a existuje tedy i v pevnĂ˝ch lĂĄtkĂĄch. Je to prĂĄvě difuze nosičů nĂĄboje se započítĂĄnĂ­m vlivu elektrickĂŠho pole, na jejĂ­mĹž zĂĄkladě mĹŻĹžeme vysvětlit efekty vznikajĂ­cĂ­ v PN přechodu a větĹĄinu procesĹŻ v polovodičovĂ˝ch součástkĂĄch vĹŻbec.

Předpokládejme, že jsme vytvořili PN přechod tak, že nalevo od počátku (pro záporná x) máme polovodič typu p a napravo od počátku polovodič typu n. Majoritními nosiči náboje v typu n jsou elektrony, v typu p díry. Vytvořením PN přechodu jsme vlastně vytvořili gradient koncentrace elektronů, který v bodě x=0 má vysokou kladnou hodnotu a gradient koncentrace děr, který v bodě x=0 má vysokou zápornou hodnotu. Ihned po vytvoření přechodu nastane tedy difuze děr z polovodiče typu p do polovodiče typu n a difuze elektronů z polovodiče typu n do polovodiče typu p. Jakmile se majoritní nosiče jednoho druhu dostanou do prostředí, kde jsou majoritními nosiči nosiče opačné polarity, prakticky okamžitě zrekombinují, tedy zaniknou z hlediska vedení proudu. Majoritní nosiče, které předifundovaly do polovodiče opačné vodivosti však odkryly náboj iontů příměsí, které jsou vázány v krystalové mřížce a nemohou se proto pohybovat. Např. díry, které předifundovaly z polovodiče typu p do polovodiče typu n, ”zanechaly” po sobě v polovodiči typu n nezkompenzovaný náboj záporných iontů třímocných příměsí a obdobně elektrony ”zanechaly” po sobě v polovodiči typu n nezkompenzovaný náboj kladných iontů pětimocných příměsí. Znamená to, že další a další difuze majoritních nosičů přes přechod se děje pod vlivem elektrického pole, neboť záporné ionty příměsí na straně polovodiče typu p působí svým přitažlivým elektrickým polem na difundující díry a obdobným efektem působí kladné ionty příměsí na straně polovodiče typu n na difundující elektrony. To má za následek, že po určité době se vytvoří rovnovážný stav a ten je právě charakterizován nedeformovanou Fermiho hladinou přes přechod PN. Je třeba si uvědomit, že celkový náboj v polovodiči zůstává zachován, tak že polovodič zůstává navenek elektricky neutrální, zmíněný přesun náboje probíhá jen v bezprostřední blízkosti přechodu PN. Kdybychom tedy připojili voltmetr na konce našeho jednorozměrného krystalu s PN přechodem, nenaměříme voltmetrem žádné napětí.

Zatím jsme diskutovali jen majoritní nosiče. Jejich pohybem vznikají vázané náboje iontů příměsí a tedy elektrické pole bránící další difusi majoritních nosičů. Jak je to však s minoritními nosiči? Ty mají opačný náboj než majoritní nosiče a vzniklé elektrické pole tedy urychluje transport minoritních nosičů přes PN přechod. Rozmyslete si, že je to skutečně tak; brzdí-li vytvořené elektrické pole např. pohyb děr ”zprava doleva”, pak jistě pohyb elektronů zprava doleva bude tímtéž polem podporován. V analogii s gravitačním polem díry zprava doleva musí ”do kopce”, zatímco elektrony zprava doleva to mají ”s kopce”. Elektrické pole v oblasti přechodu tedy ”odsává” minoritní nosiče přes přechod, čímž vzniká gradient koncentrace minoritních nosičů v blízkosti přechodu, který ”se stará” o to, aby minoritní nosiče z míst vzdálenějších přechodu k němu difundovaly. Vznikne opět rovnovážný stav, kdy proud děr jako majoritních nosičů z typu p do n je kompenzován proudem děr jako minoritních nosičů z n do p a obdobně pro elektrony. Vidíme, že minoritní nosiče zde plní velmi významnou úlohu kompenzace zbytku proudu majoritních nosičů (z chvostu distribuční funkce), které se přece jenom přes vytvořenou potenciálovou bariéru dostanou.

Důležité je si uvědomit, že proud minoritních nosičů je nasycený, tj. elektrické pole v oblasti přechodu PN je natolik velké, že stačí odsát všechny minoritní nosiče, které se do blízkosti přechodu dostanou (podíváte-li se o několik odstavců výše, uvidíte, že tento proud je dán difusním koeficientem minoritních nosičů příslušného druhu a gradientem jejich koncentrace; tento gradient však nemůže být příliš veliký, neboť koncentrace minoritních nosičů je malá a proto ani celkový difuzní proud nebude velký). Z toho plyne, že tento nasycený proud minoritních nosičů nebude prakticky záviset na výšce potenciálové bariéry mezi stranou p a stranou n.

Přiložíme-li nyní na PN přechod napětí v takové polaritě, že strana p je kladná a strana n záporná (tzv. propustný směr), budeme působit naším vtištěným elektrickým polem proti elektrickému poli, které se přes přechod vytvořilo a tedy budeme vytvořenou difuzní potenciálovou bariéru snižovat. Uvážíme-li tvar Maxwell- Boltzmannovské rozdělovací funkce budeme tím exponenciálně zvyšovat počet majoritních nosičů z obou stran, které se přes bariéru dostanou. Přitom, jak jsme si uvedli, proud minoritních nosičů nebude touto naší akcí významně ovlivněn. Přiložíme-li napětí v opačné polaritě (tzv. závěrný směr), budeme naopak potenciálovou bariéru, která brání průchodu majoritních nosičů přes přechod zvyšovat a počet majoritních nosičů přes přechod se bude (opět exponenciálně) snižovat. Opět při této akci neovlivníme významně množství minoritních nosičů, které se přes přechod dostávají. To znamená, že při dostatečně vysokém napětí této polarity zmenšíme proud majoritních nosičů prakticky na nulu a přes přechod poteče pouze proud minoritních nosičů. Snadno se dá odvodit tzv. diodová rovnice,

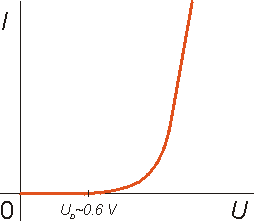
I=I_o(exp(eV/kT)-1),

kde V je napětí na přechodu (kladné v propustném směru) a I_o tzv. zbytkový proud. Při odvozování této rovnice je třeba předpokládat, že veškeré z vnějšku přiložené napětí se objeví na přechodu, jinak řečeno, že proudy v propustném směru budou tak malé, aby nezpůsobily ohmické úbytky při průchodu proudu polovodičem od kontaktu k přechodu. Zhruba se dá říci, že to je splněno pro proudy až do cca 1 mA a v tomto rozmezí proudů může tedy dioda sloužit jako prvek s exponenciální voltampérovou charakteristikou. Pro vyšší proudy pak ohmické úbytky převáží, uvedená diodová rovnice přestává platit a je nahrazena prostým Ohmovým zákonem, kde v roli odporu vystupuje odpor materiálu diody (představíme-li si odpor materiálu diody a odpor přechodu jako dva odpory v serii, pak při malých proudech bude odpor přechodu podstatně větší než materiálu a bude záviset na napětí, při vyšších proudech se odpor materiálu podstatně nezmění a odpor přechodu klesne v podstatě na nulu). VA charakteristika reálné diody je na obr. 3.12a.

obr. 3.12a

---

---