Rezonance

Říkáme, že střídavý elektrický obvod je v rezonanci, jestliže napětí U přiložené na obvod a proud I protékající obvodem jsou ve fázi. Tedy při rezonanci je celková komplexní impedance obvodu reálná a účiník je roven jedné.

Sériová rezonance

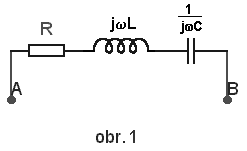RLC obvod na obr. 1 má komplexní impedanci Z=R+j(ω L-1/ω C)=R+jX. Obvod je v rezonanci, jestliže X=0, tj. ω L=1/ω C a tedy . Jelikož je ω =2π f, je rezonanční frekvence dána vztahem .

Na obr. 2 je znázorněna absolutní hodnota Z a jejích tří složek rezistance R, induktance X_L a reaktance X_C jako funkce ω. Při ω=ω₀ se rovnají induktance a reaktance a Z=R. Při rezonanci má funkce Z=Z(ω) minimum. Jelikož I=U/Z, je pak proud obvodem maximální.

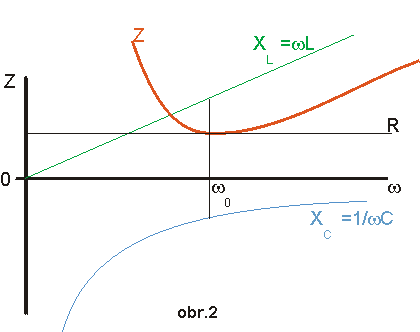Při frekvencích ω <ω₀ je reaktance větší než induktance a úhel mezi reálnou osou a impedancí je záporný. Je-li rezistance malá, úhel se s frekvencí mění rychleji (obr. 3). Když se frekvence blíží nule, blíží se úhel -π/2. Při frekvencích ω >ω₀ je induktance větší než reaktance a úhel je kladný. Když je ω >>ω₀, úhel se blíží +π/2.

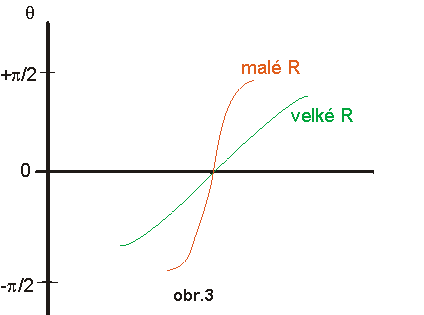Na obr. 4 je ještě zachycena admitance Y=1/Z jako funkce Y=Y(ω). Opět je vidět, že proud obvodem je větší při menší rezistanci.

Paralelní rezonance

Mějme paralelní obvod s ideálními prvky R, L, C v jednotlivých větvích (obr. 5).
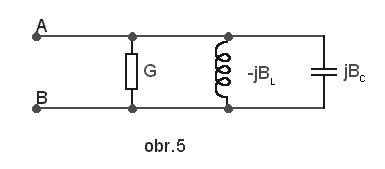celková admitance Y=G+j(ω C-1/ω L)=G+jB, kde B=B_C-B_L, B_C=ω C, B_L=1/ω L. Obvod je v rezonanci právě tehdy, když B=0, tedy ω C=1/ω L a . Stejně jako u sériového RLC obvodu je rezonanční frekvence dána vztahem .

Na obr. 6 je znázorněna absolutní hodnota Y a její tři složky G, B_L a B_C jako funkce ω. Jelikož v rezonanci je admitance minimální a I=UY, má proud v rezonanci minimální hodnotu.

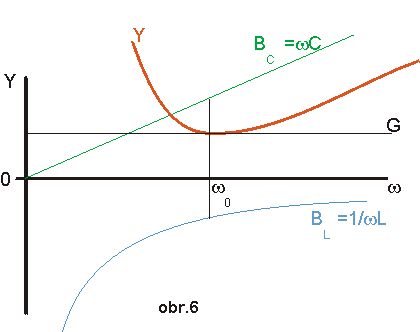Paralelní rezonance v obvodu se dvěma větvemi

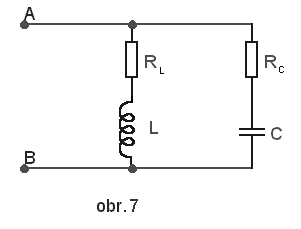
V obvodu na obr. 7 je celková admitance Y rovna součtu admitancí v jednotlivých větvích.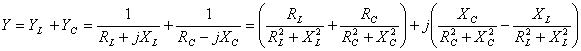

Obvod je v rezonanci, když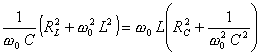

a tedy

. Řešením této rovnice získáme výsledný vztah

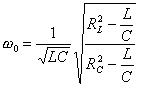Rezonanční frekvence tohoto obvodu se od rezonanční frekvence paralelního spojení čistých prvků R, L, C liší faktorem .

Jelikož frekvence je kladné reálné číslo, má obvod rezonanční frekvenci jen v případě, že výrazy R_L²-L/C a R_C²-L/C jsou oba kladné nebo oba záporné. Jsou-li oba rovny nule, je obvod v rezonanci při všech frekvencích.

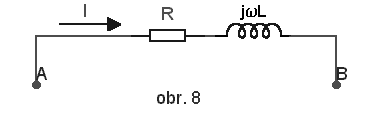
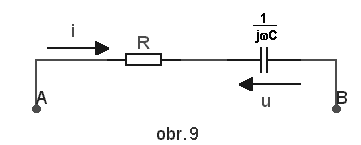
Činitel jakosti Q

Činitel jakosti cívky, kondenzátoru a obvodu se definuje jako Q=2π E/E_T, kde E je maximální akumulovaná energie na prvku a E_T je energie přeměněná na prvku za jednu periodu.

V RL obvodu (obr. 8) a v RC obvodu (obr. 9) je energie disipovaná za periodu dána součinem průměrného výkonu na rezistoru a periody T=1/f, tedy .

V RL obvodu je maximální akumulovaná energie

, tedy

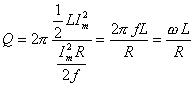V RC obvodu je , tedy .

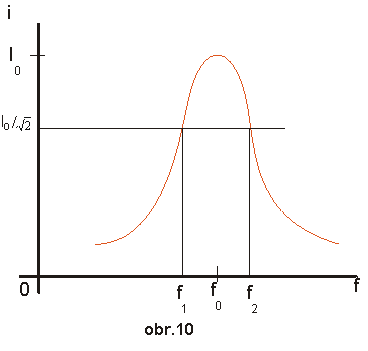V sériovém RLC obvodu v rezonanci se akumuluje konstantní množství energie. Když je napětí na kondenzátoru maximální, je proud cívkou nulový a obecně . Z toho je . Na obr. 10 je proud v sériovém RLC obvodu jako funkce frekvence f. Při f₀=ω ₀/2π prochází obvodem maximální proud I₀.

Jelikož průměrný výkon dodávaný do obvodu je P=I²R, při proudu

je výkon roven polovině maximálního výkonu při frekvenci f₀ . Body odpovídající frekvencím f₁ a f₂ nazveme body polovičního výkonu. Rozdíl mezi těmito dvěma body, měřený v hertzích, se nazývá šířka pásma BW.

Nyní můžeme činitel jakosti napsat jako podíl rezonanční frekvence a šířky pásma, .

Rezonanční frekvence ω₀ je geometrickým průměrem ω₁ a ω₂ , a .

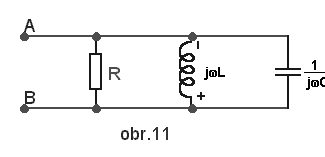
V paralelním obvodu se třemi větvemi na obr. 11 se v rezonanci akumuluje konstantní množství energie. Je-li proud cívkou maximální, je napětí na kondenzátoru nulové a obecně 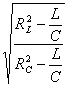. 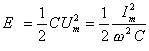Tedy .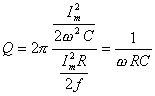