6.1.1. Metody amplitudové modulace

Po vysvětlení principu amplitudové modulace, vysvětleme si nyní jakým způsobem můžeme prakticky dosáhnout toho, abychom vytvořili amplitudově modulovaný signál. Z principu amplitudové modulace plyne, že amplitudově modulovaný signál vytvoříme vynásobením signálu reprezentujícího amplitudu proměnnou v rytmu přenášené informace a signálu nosné vlny. Toto vynásobení je možné provést přímo v analogových obvodech k tomu určených, tzv. násobičkách. Takovou násobičkou může být tranzistorový zesilovač, jehož zesílení učiníme úměrné velikosti napájecího napětí, viz obrázek 6.2,

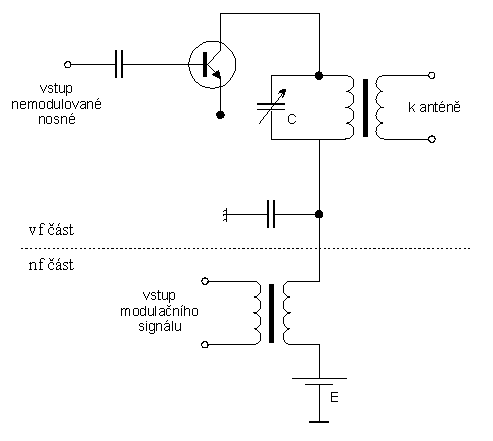
obr. 6.2.

na kterém je znázorněn tranzistorový zesilovač ve třídě C, to jest s takovým nastavením pracovního bodu, aby proud tranzistorem tekl po dobu kratší, než polovina periody. Zesilovač pracuje do rezonančního obvodu LC, který kmitá samostatně na své rezonančním kmitočtu a proudové impulsy od tranzistoru jen kompenzují ztráty vzniklé v rezonančním obvodu nenulovým odporem cívky a svodem kondenzátoru. Je to systém velmi obdobný mechanickému kyvadlu, které kývá se svou vlastní frekvencí, a abychom udrželi konstantní amplitudu oscilací, tedy kompenzovali ztráty třením, ”šťouchneme” každou periodu trochu do kyvadla, např. při rozběhu z jedné krajní polohy. Bude-li tento ”šťouch” proveden větší silou, rozkmitáme kyvadlo na větší amplitudu. Podobným způsobem se chová obvod na obrázku 6.2. Signál na vstupu tranzistoru (RF input) otevírá tranzistor jen po krátký úsek periody a otevřený tranzistor pak provádí proudový ”šťouch” do oscilačního obvodu, aby tak kompenzoval ztráty v tomto oscilačním obvodu. Zvýšíme-li napájecí napětí tranzistoru, zvýšíme tím i proud tranzistorem po dobu jeho otevření a následně i amplitudu kmitů rezonančního obvodu. Tento proces je v určitých mezích napájecího napětí lineární, tj. amplituda kmitů oscilačního obvodu je úměrná napájecímu napětí. Na obrázku je znázorněno, jak je modulační napětí pomocí transformátoru přivedeno do série s napájecím napětím. Označíme-li zesílení zesilovače A, pak můžeme v oblasti, kde závislost zesílení na napájecím napětí E je lineární, napsat A=konst.E. Výstupní napětí tohoto stupně, tj. amplituda napětí na oscilačním obvodu, je tedy jednak úměrná vstupnímu napětí nosné vlny, jednak napájecímu napětí, na které se sériově přičítá modulační napětí:

U_výst = konst · U_vst · E.

Dosadíme-li za E součet s modulačním napětím, tedy

E = E₀ · [ 1+α·cos(ω_Mt) ]

(kde E₀ je původní napájecí napětí stupně, kdy modulační napětí je rovno nule) a za U_vst napětí nosné vlny,

U_vst = konst · cos(ω_Nt)

vidíme, že výstupní napětí pak bude dáno jako:

U_výst = konst · cos(ω_Nt) · [ 1+α·cos(ω_Mt) ],

tedy amplitudově modulovanou nosnou vlnu tak, jak jsme chtěli. Tomuto typu modulátoru se říká kolektorový modulátor (původně s elektronkami to byl anodový modulátor) a reprezentuje nám přímo násobičku dvou signálů.

Násobení signálů můžeme provést i nepřímo, na nelineární impedanci. Představme si nelineární prvek, tj. prvek s nelineární voltampérovou charakteristikou, například diodu s přechodem PN. Voltampérová charakteristika této diody je teoreticky exponenciální, pro malé signály je však možné exponenciální charakteristiku rozvinout do Taylorovy řady a zanedbáním vyšších členů aproximovat teoretickou charakteristiku parabolou, tedy křivkou, jejíž analytické vyjádření je

i = a₀ + a₁v + a₂v²,

kde i je proud diodou a v napětí na diodě. Předpokládejme dále, že na diodu připojíme napětí, které dostaneme prostým součtem napětí nosné vlny a modulačního napětí,

v = A_N · cos(ω_Nt) + A_M · cos(ω_Mt).

Po dosazení a jednoduché úpravě dostaneme, že proud diodou bude vypadat následujícím způsobem:

i = a₀ + (a₂/2)(A_N²+A_M²) +
+ a₁ [ A_Ncos(ω_Nt) + A_Mcos(ω_Mt) ] + (a₂/2) [ A_N²cos(2ω_Nt) + A_M²cos(2ω_Mt) ] +
+ a₂A_NA_M [ cos(ω_N + ω_M)t + cos(ω_N - ω_M)t ].

Předpokládáme-li, jak je obvyklé, že ω_N >> ω_M, můžeme pomocí vhodných filtrů odfiltrovat z tohoto signálu všechny frekvence kromě pásma mezi ω_N-ω_M a ω_N+ω_M. Proud diodou necháme procházet rezistorem o hodnotě r, abychom převedli proud diodou na napětí a dostaneme

r · i = r · a₁ A_N [ cos(ω_Nt) + (a₂A_M/a₁) ( cos(ω_N+ω_M)t + cos(ω_N-ω_M)t ) ].

Vytvořili jsme tedy také amplitudově modulovaný signál. Modulátory založené na tomto principu využívají obvykle nelineární vstupní charakteristiky tranzistoru. Vzhledem k tomu, že jsou nutné dodatečné filtry a že nelinearita vstupní charakteristiky může být vyjádřena i členy vyššího než druhého řádu (což se projeví v dodatečném zkreslení amplitudově modulovaného signálu),využívají se tyto, tzv. mřížkové modulátory mnohem méně často než kolektorové (anodové).

Detekce amplitudově modulovaných signálů