7.2.2. Booleovy algebry a jejich vlastnosti
V předcházejícím odstavci jsme se zmínili, že množina dvojstavových proměnných spolu s operacemi logického součtu, součinu a negace tvoří tzv. Booleovu algebru. Pojem Booleovy algebry je však obecnější, takže námi uvedená množina je jen její speciální případ. Vyvinul se v návaznosti na analogii mezi množinovými operacemi sjednocení a průnik a aritmetickými operacemi sčítání a násobení. Rozsah a důležitost této analogie objasnil jako první britský matematik George Boole (1815-1864), který položil základy algebraické teorie množin před více než 100 lety.
Obecně je Booleova algebra definována takto:
Booleova algebra je množina B prvků a, b, c, ... s následujícími vlastnostmi:
a) B má dvě binární operace, ∧ (průnik) a ∨ ( sjednocení ), která jsou
idempotentní a ∧ a = a ∨ a = a
komutativní a ∧ b = b ∧ a , a ∨ b = b ∨ a
asociativní a ∧ (b ∧ c) = (a ∧ b) ∧ c
a ∨ (b ∨ c) = (a ∨ b) ∨ c
b) tyto operace vyhovují zákonům absorpce
a ∧ (b ∨ b) = a ∨ (a ∧ b) = a
c) obě operace jsou distributivní
a ∧ ( b ∨ c ) = ( a ∧ b ) ∨ ( a ∧ c )
a ∨ ( b ∧ c ) = ( a ∨ b ) ∧ ( a ∨ c )
d) obsahuje univerzální ohraničení 0 a 1 , která vyhovují vztahům
0 ∧ a = 0 , 0 ∨ a = a ,
e) B má unární operaci ![]()
tvoření komplementu s vlastnostmi:
![]() a
a
![]()
Dále lze z definice dokázat řadu vlastností Booleových algeber. Jsou to především zobecněné distributivní zákony:
![]()
pro x, a1, a2 , ..., an ∈ B
![]()
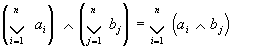
pro ai, bj ∈ B; i = 1, 2, ..., n; j = 1, 2, ..., m, kde
![]()
Dále se dají dokázat zobecněné de Morganovy zákony
![]()
![]()
Pro další výklad budeme potřebovat následující
větu. Každý Booleovský výraz (tj. výraz utvořený pomocí operací "∧", "∨" a "¯"), ve
kterém se vyskytuje n prvků x1, .., xn se dá vyjádřit právě jedním způsobem jako sjednocení
tzv. minimálních booleovských polynomů, tj. výrazů tvaru ![]() , kde buď ai = Xi:
nebo ai =
, kde buď ai = Xi:
nebo ai = ![]() . Tomuto tvaru Booleovského výrazů (nebo Booleovské funkce)
se říká disjunktivní kanonický tvar. Minimálním booleovským polynomům se často
říká mintermy (z anglického minimal polynomial term). Důkaz této věty není
složitý, avšak vybočuje již z rámce těchto skript. Čtenář jej může najít
v běžně dostupné literatuře.
. Tomuto tvaru Booleovského výrazů (nebo Booleovské funkce)
se říká disjunktivní kanonický tvar. Minimálním booleovským polynomům se často
říká mintermy (z anglického minimal polynomial term). Důkaz této věty není
složitý, avšak vybočuje již z rámce těchto skript. Čtenář jej může najít
v běžně dostupné literatuře.
Dá se ukázat, že pro n proměnných X1,
..., Xn existuje 2n různých
minimálních polynomů X1 X2 ...Xn,
![]() 1X2... Xn,
1X2... Xn,
![]() .
Z těchto polynomů pak můžeme utvořit celkem
.
Z těchto polynomů pak můžeme utvořit celkem ![]() kombinací,
což je také celkový počet různých booleovských funkcí n proměnných, protože
podle právě uvedené věty je vyjádření v minimálních polynomech
jednoznačné.
kombinací,
což je také celkový počet různých booleovských funkcí n proměnných, protože
podle právě uvedené věty je vyjádření v minimálních polynomech
jednoznačné.
Pro úplnost je třeba ještě uvést, že právě tak, jako pomocí minimálních
polynomů, se dá každá Booleovská funkce vyjádřit jednoznačně jako průnik tzv.
maximálních booleovských polynomů (maxtermů), což jsou výrazy tvaru ![]() ,kde opět buď ai=Xi
nebo ai =
,kde opět buď ai=Xi
nebo ai = ![]() .
.
Protože je však zřejmé, že lze pomocí de
Morganových zákonů snadno převádět tvar mintermový na tvar maxtermový
(vyjádříme-li nejprve inversi požadované funkce F v jednom tvaru a pak
aplikujeme de Morganův zákon, abychom získali ![]() tj. F), nenachází maxtermový tvar tak široké využití jako
mintermový.
tj. F), nenachází maxtermový tvar tak široké využití jako
mintermový.
Z definice Booleovy algebry plyne, že množina dvoustavových (logických) proměnných tvoří Booleovu algebru. Logický součin je průnikem a logický součet sjednocením které jsou:
1. komutativní
A + B = B + A
A . B = B . A
2 .asociativní
A + B + C = A + (B + C) = (A + B) + C
A . B . C = A . (B . C) = (A . B) . C
3. distributivní
A . (B + C) = A.B + A.C
A + (B . C) = (A + B) . (A + C)
Unární operace je tvoření inverze: A → ![]() vytvoří
negovaný komplement logické proměnné.
vytvoří
negovaný komplement logické proměnné.
T a b u l k a 5.2
| Funkce | Název funkce | Logický člen | Algebraický výraz |
| f0 | konstanta | 0 | |
| f1 | logický součet | NEBO(OR,ODER) | a + b |
| f2 | implikace | ||
| f3 | implikace | ||
| f4 | Shefferova funkce | NAND | |
| f5 | logický součin | A ( AND,UND) | ab |
| f6 | inhibice | ||
| f7 | inhibice | ||
| f8 | Pierceova funkce | NOR | |
| f9 | identita | a | |
| f10 | identita | b | |
| f11 | ekvivalence | ||
| f12 | neekvivalence | Exclusive OR | |
| f13 | negace | NE (NOT,NICHT) | |
| f14 | negace | NE (NOT,NICHT) | |
| f15 | konstanta | 1 |
Pomocí základních operací logického součtu součinu a negace můžeme pro jednu logickou proměnnou vytvořit devět základních identit:
1. A =
identita invert
2. A. 1 = A
3. A. 0 = 0 identita logického součinu
4. A.A = A
5.
6. A+1 = 1
7. A+0 = A identita logického součtu
8. A+A = A
9.
Dále v Booleově algebře logických proměnných můžeme de Morganovy teorémy vyjádřit pro dvě logické proměnné ve tvaru:
![]()
![]()
Uvedených vztahů a identit můžeme využít ke zjednodušení složitějších logických funkcí.
Jak bylo uvedeno v obecné části z Booleovy algebry plyne, že dvěma logickými proměnnými lze realizovat celkem 24 = 16 funkcí, z nichž některým se dostalo zvláštního pojmenování. Přehled těchto funkcí je uveden v tabulce 5.2.
Množina logických operací není ovšem jediná Booleovská algebra. Čtenář si může snadno ověřit, že například podmnožiny určité množiny M, ve které je definován průnik, sjednocení a tvoření komplementu způsobem běžným pro tyto množinové operace, tvoří rovněž Booleovu algebru.