Homogenní vedení

Homogenní vedení jest vedení se spojitě rozloženými parametry: na délkovou jednotku má odpor R, indukčnost L, kapacitu C a svod G. Příčný rozměr jest zanedbatelně malý vzhledem k vlnové délce příslušné frekvence budícího signálu, avšak délkový rozměr vlnovou délku převyšuje, nebo jest s ní srovnatelný. Prakticky je homogenní vedení provedeno buď jako dvoulinka, nebo koaxiální kabel. Aplikujeme-li na úsek homogenního vedení délky  (viz obr. D1.1) Kirchhoffovy zákony, dostaneme

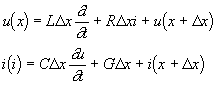
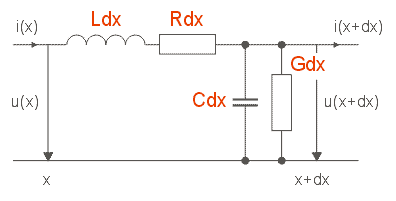
Obr. D1.1  Homogenní vedení

Provedením limitního přechodu pro  dostaneme tzv. telegrafní rovnice.

            (D1)

          (D2)

 Jde-li o ustálené stavy ve vedení buzeném sinusovým signálem použijeme běžné symbolické metody, avšak amplitudu považujeme za funkci souřadnice x:  (nebo ), takže (D1) a (D2) přejdou v rovnice pro symboly napětí a proudu:

          (D3)

          (D4)

jejichž řešením jest

                  (D5)

          (D6)

kde

a

              (charakteristická impedance)

 Dostaneme tedy obecně tlumené vlny, které se šíří po vedení. V případě bezeztrátového vedení (idealizace) R = 0, G = 0 jest  imaginární a vlny jsou netlumené, veličina  jest reálná (vlnový odpor). Konstanty A, B jsou obecně závislé na délce vedení a impedanci připojené na konci vedení. Určete si konstanty A, B pro případ vedení délky l zakončeného impedancí Z, přiložené napětí pro x = 0 budiž U₀. Dále musí platit U (l) = ZJ (l).

Dostanete: A = U₀ 

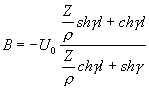
Rovnice (D5), (D6) se dají pak upravit na výhodný tvar:

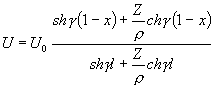          (D7)

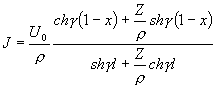          (D8)

Probereme si některé význačné případy. Pro větší přehlednost výsledků budeme uvažovat bezeztrátové vedení, tj. :

 jest imaginární a vlny jsou netlumené, vlnový odpor (charakteristická impedance) jest reálný  .

1. případ:

vedení jest zakončeno charakteristickou impedancí, takže . Rovnice (D7) a (D8) se upraví na

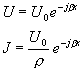
a odtud pro skutečné hodnoty napětí u(x,t) a proud i(t,x)

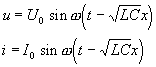
Vedením se tedy šíří běžící vlna rychlostí , energie dodaná vnějším zdrojem se pohltí v zátěži. Nenastane odraz vln na konci vedení.

 Zjistěte si, jak se tento výsledek změní, bude-li vedení ztrátové, tj. . Bez počítání lze říci, že odraz opět nenastane, avšak energie dodávaná zdrojem se částečně pohltí ve vedení, částečně v zátěži.

2. případ:

vedení jest na konci zkratováno, tj. položíme Z = 0. Z rovnic (D7), (D8) dostaneme nyní

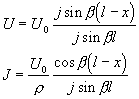
a odtud pro skutečné hodnoty u(x,t) a  i(t,x)

    ,

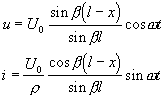což jsou stojaté vlny napětí a proudu. V souladu s fyzikální skutečností má napětí na konci zkratovaného vedení ( x = l ) uzel a proud kmitnu. Můžeme si představiti, že tyto stojaté vlny vznikly superpozicí vlny přímé a odražené. Pro vedení ztrátové se můžete přesvědčit výpočtem, že tlumená vlna se rozdělí na přímou a odraženou.

3. případ:

vedení jest na konci otevřené, tj. a z rovnic (D7), (D8) plyne

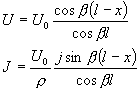
a dostáváme tedy opět stojaté vlny napětí a proudu

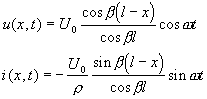
 Prakticky jest často důležité znát vstupní impedanci homogenního vedení, danou poměrem .

Z rovnic (D7), (D8) dostaneme obecně

         (D9)

Uvědomíme si, že při zatížení vlnovým odporem jest vstupní impedance  . Odvoďte výrazy pro Z₀ při zkratovaném a otevřeném homogenním vedení délky l (bezeztrátovém) a snažte se pochopit fyzikální a praktický význam.

 V literatuře se setkáváme též se symbolickým reflexním koeficientem, který vyjadřuje poměr symbolů napětí (proudu) odražené vlny ku přímé vlně.

 Vyjádříme si řešení telegrafních rovnic pro symboly napětí a proudu takto:

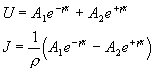
Jestliže označíme U(0) = U₀, J(0) = J₀  dostaneme

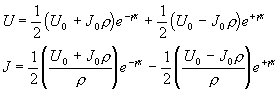
Vlna se záporným exponentem je přímá, vlna s kladným je odražená. (To se dá snadno nahlédnout, přejdeme-li od symbolů ke skutečným hodnotám. ) Na konci vedení délky l jest reflexní koeficient dán výrazem

takže

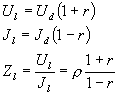
          (D10)

hlavní stránka