Základní energetické vztahy

Elektronická zařízení v ultravysokofrekvenční oblasti jsou  založena na interakci elektronů s vysokofrekvenčními poli. Vzhledem k tomu, že doba, po kterou elektron pobývá ve vnějším vysokofrekvenčním poli je v tomto oboru srovnatelná nebo větší než perioda vysokofrekvenčního pole, nemůžeme vystačiti s kvazistacionárními úvahami. Elektrony nereagují na změny elektromagnetického pole okamžitě, projevuje se setrvačnost. Z energetického hlediska mohou nastat dvě možnosti:

• elektrony přijmou energii od vysokofrekvenčního pole (princip urychlovače)
• elektrony předají svou energii vysokofrekvenčnímu poli (princip zesilovače a generátoru).

V dalším budeme vycházet z Maxwellových rovnic ve tvaru

		(5.1.1)
		(5.1.2)
		(5.1.3)
		(5.1.4)

a z pohybové rovnice volného elektronu

                  (5.1.5)

Mezi hustotou proudu i a hustotou náboje r bude platit dále vztah

a z rovnic (5.1.2) a (5.1.4) dostaneme ještě pro naše úvahy důležitou rovnici kontinuity

              (5.1.6)

Soustavu rovnic (5.1.1) až (5.1.4) lze řešit, známe-li funkce a . Tato podmínka není splněna, protože hustota proudu a hustota náboje elektronů, které vstupují do interakce s elektromagnetickými poli, je těmito poli ovlivněna. A naopak pole, v nichž k interakci dochází, jsou deformována prostorovým nábojem elektronů. Tato situace vyžaduje speciální metody, vytvoření přibližných modelů a určité představivosti.

V oblasti nižších frekvencí je možné generátor samobuzených kmitů realizovat pomocí vhodné zpětné vazby. U LC generátoru jde o to, aby ztráty způsobené tím, že reálný LC obvod je tlumený, byly nahrazovány vhodným odběrem energie z vnějšího stejnosměrného zdroje napětí, z něhož si obvod podle potřeby energii „sám odebírá“. Tato situace se dá přenést i do oblasti velmi vysokých frekvencí: resonátor s daným činitelem jakosti Q má určité ztráty, které jsou způsobeny konečnou vodivostí stěn, vyzařováním energie štěrbinou apod. Ty mohou být nahrazeny na úkor kinetické energie elektronů procházejících resonátorem. Kinetická energie je dodávána elektronům z vnějšího zdroje stejnosměrného napětí. 

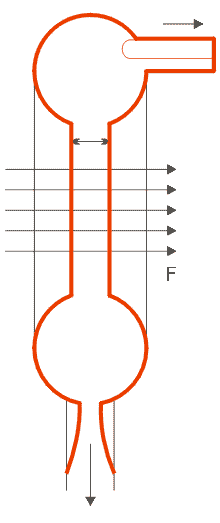	Jestliže dochází k takové interakci v objemu V, hraje důležitou roli výkon vzájemného působení elektronů s polem daný výrazem       (5.1.7) Výkon vyzářený z daného objemu V přes uzavřenou plochu F je kde  je Poyntingův vektor.  Zákon zachování energie lze pak psát ve tvaru kde Podle zákona zachování energie dostaneme, že
Obr. 5.1.1  Resonátor buzený svazkem elektronů o objemu V obklopený plochou F

Vypočítáme-li střední hodnoty ze jednu periodu, dostaneme

neboť

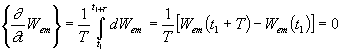
 je střední výkon vycházející z objemu V, který se skládá jednak z výkonu spotřebovaného na zahřátí a jiné ztráty, jednak z výkonu, který z resonátoru vystupuje a postupuje dále:

takže

což znamená, že v rovnovážném stavu se střední výkon interakce elektronů s polem spotřebuje na tepelné ztráty v resonátoru a na výkon do zátěže. Podmínka, která musí být vždy splněna je

      (5.1.8)

Toto je podmínka nutná pro buzení resonátoru a je ekvivalentní podmínce pro vznik samobuzených kmitů. Abychom získali názornější představu o tom, co tato podmínka vyjadřuje, upravíme vhodně výraz a pak provedeme integraci přes objem V. Vzhledem k tomu, že

 a

dostaneme

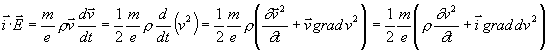
Avšak a vzhledem k rovnici kontinuity (5.1.6) je

Zavedeme si hustotu kinetické energie elektronů , kde n je koncentrace elektronů a platí , takže

Provedením integrace

Při vystřeďování vychází

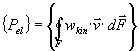
Podmínka samobuzení nyní požaduje, aby

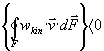      (5.1.8´)

to znamená, že průměrný tok kinetické energie elektronů plochou ohraničující objem interakce musí být záporný: elektrony průměrně dopraví do objemu více energie, než jí odnesou. Neznamená to ovšem, že každý individuální elektron je vysokofrekvenčním polem brzděn, ale celkový efekt je brzdění převládající nad urychlováním.

hlavní stránka | další >>>