Základní vlastnosti dutinových rezonátorů obecného tvaru.
Charakteristické frekvence. Činitel jakosti.
Dutinové resonátory mají v oblasti
mikrovln a kratších (optických) podobnou funkci jako resonanční obvody v
radiofrekvenčním oboru.
 |
Nyní se budeme zabývat podrobněji vlastnostmi
dutinových resonátorů.
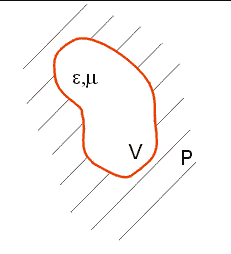
Nejprve budeme zkoumat elektromagnetické pole v
ideálním dutinovém resonátoru, což je dutina vyplněná vakuem (nebo
bezeztrátovým dielektrikem) zcela uzavřená ideálně vodivými stěnami libovolného
tvaru, objemu V a plochy P,
(obr. 4.1.1).
Platí:
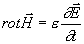 (4.1.1)
(4.1.1)
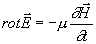 (4.1.2) (4.1.2)
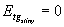 (4.1.3)
(4.1.3)
|
|
Obr. 4.1.1 Ideální dutinový resonátor
|
Zajímá nás otázka, jaké elektromagnetické pole uvnitř dutiny V
může existovat. Aplikujeme tedy na rovnici (4.1.2) operaci rot
a máme
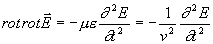 (4.1.4)
(4.1.4)
Řešení budeme psát ve tvaru
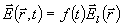 , takže z (4.1.4) dostaneme
, takže z (4.1.4) dostaneme
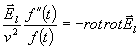
Vzhledem k tomu, že pravá strana nezávisí na čase musí být
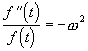 .
.
Označíme
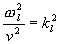 a
dostaneme
a
dostaneme
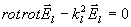 (4.1.5)
(4.1.5)
Z rovnice (4.1.5) vyjádříme
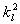 , čímž získáme jednak
obecný vzorec, který určuje charakteristickou frekvenci pomocí prostorové
struktury pole v dutině, a také dokážeme, že
, čímž získáme jednak
obecný vzorec, který určuje charakteristickou frekvenci pomocí prostorové
struktury pole v dutině, a také dokážeme, že
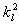 je
pozitivní
(existují kmity). Postupujeme následujícím způsobem:
je
pozitivní
(existují kmity). Postupujeme následujícím způsobem:
rovnici (4.1.5) násobíme
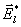 zleva a integrujeme
přes objem resonátoru:
zleva a integrujeme
přes objem resonátoru:
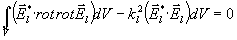
Použitím vzorce
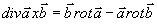
a s přihlédnutím k tomu, že
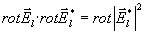
máme
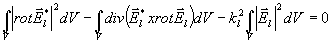
Avšak
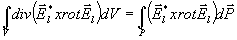
Z okrajových podmínek vyplývá, že vektory
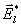 a
a
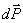 jsou na stěnách
rovnoběžné, takže integrál přes plochu P je nulový a pro
ideální resonátor dostaneme
jsou na stěnách
rovnoběžné, takže integrál přes plochu P je nulový a pro
ideální resonátor dostaneme
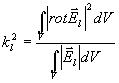 (4.1.6)
(4.1.6)
Tím jsme dostali výraz pro
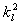 (a tedy také pro
(a tedy také pro
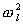 ), který
je kladný. To znamená, že existují netlumené kmity
na charakteristických frekvencích
), který
je kladný. To znamená, že existují netlumené kmity
na charakteristických frekvencích
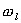 :
:
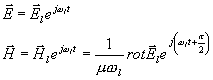
Dále se dá snadno dokázat, že střední hodnoty energie elektrického a magnetického pole
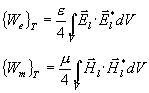
jsou stejné
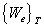 =
=
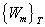
Při konečné vodivosti stěn jsou volné kmity v resonátoru
provázeny ztrátami energie. I když neuvažujeme dielektrické ztráty a ztráty
vyzařováním v reálném resonátoru. Jsou-li stěny ztrátové, neplatí již
(4.1.3). Z
toho plyne, že vektory
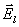 a
a
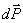 nejsou rovnoběžné a
pro
nejsou rovnoběžné a
pro 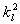 dostaneme po jednoduchých úpravách
dostaneme po jednoduchých úpravách
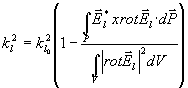
kde
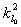 označujeme nyní výraz
(4.1.6) pro ideální resonátor.
označujeme nyní výraz
(4.1.6) pro ideální resonátor.
Dosazením za 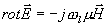
dostaneme
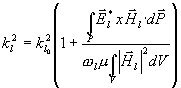
Dále použitím vztahů známých z výpočtu útlumu v reálném vlnovodu
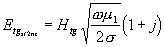
kde
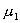 je permeabilita
vodivé stěny, a použitím hloubky skinu
je permeabilita
vodivé stěny, a použitím hloubky skinu
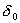
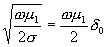
dostaneme
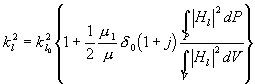
Vzhledem k tomu, že
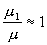 , poměr integrálů
, poměr integrálů
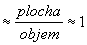 a že
a že
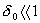 můžeme reálnou část
druhého členu v kroucené závorce zanedbat vedle jedné. Potom
můžeme reálnou část
druhého členu v kroucené závorce zanedbat vedle jedné. Potom
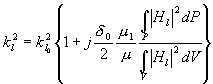 (4.1.7)
(4.1.7)
Zcela analogicky můžeme psát pro
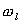 :
:
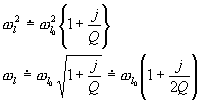
kde
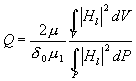 (4.1.8)
(4.1.8)
je činitel jakosti.
Vzorec (4.1.8) umožňuje jeho výpočet,
je-li známa struktura magnetického pole uvnitř ideálního rezonátoru.
Přesvědčíme se snadno, že Q podle (4.1.8)
je
zobecněním pojmu činitele jakosti u LRC obvodu.
Zde máme:
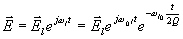
U paralelního LRC obvodu je útlumový faktor
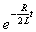 . Dosadíme-li podle
definice
. Dosadíme-li podle
definice
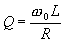 , dostaneme analogický výsledek
, dostaneme analogický výsledek
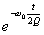 .
.
Poznámka: můžeme činitele jakosti 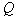 vyjádřit bez použití analogie s LRC obvodem. Zjistili jsme, že amplituda
elektrického nebo magnetického pole klesá jako
vyjádřit bez použití analogie s LRC obvodem. Zjistili jsme, že amplituda
elektrického nebo magnetického pole klesá jako
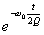 , takže příslušná energie bude
klesat jako
, takže příslušná energie bude
klesat jako
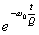 .
.
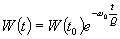
odkud úbytek energie za jednotku času
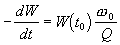 a
a
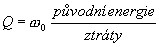
Zatímco výpočet 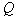 podle
(4.1.8) je pro
geometricky složitější dutiny obtížný, lze snadno odhadnout řádovou velikost
činitele jakosti, neboť
podle
(4.1.8) je pro
geometricky složitější dutiny obtížný, lze snadno odhadnout řádovou velikost
činitele jakosti, neboť
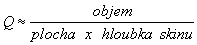
Příklad: pro
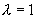 cm a
cm a
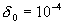 cm je
cm je 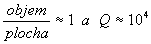 .
.
hlavní stránka

![]() (4.1.1)
(4.1.1)![]() (4.1.2)
(4.1.2)![]() (4.1.3)
(4.1.3)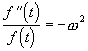 .
. 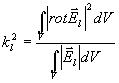 (
(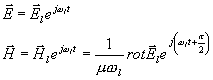
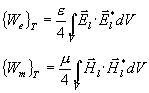
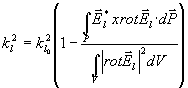
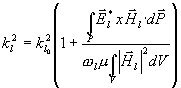
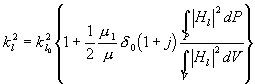
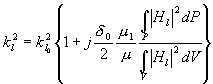 (
(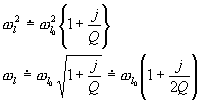
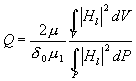 (4.1.8)
(4.1.8)