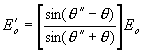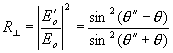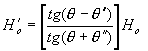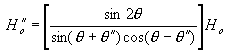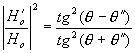Odraz kolmo dopadající vlny od ideálně vodivé stěny
Předpokládejme, že vlna šířící se
ve směru osy z bude míti v rovině z = 0 ideálně vodivou rovinu v cestě. Vlna se
pak musí odrážet ze dvou důvodů:
1. jen jednou vlnou nelze splnit okrajové
podmínky
2. v ideálním vodiči se nemůže spotřebovat energie a tak veškerá
energie „přinesená“ dopadající vlnou, musí být „odnesena“ odraženou
vlnou:
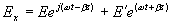 . Pro z = 0 musí být Ex = 0 pro libovolné
t.
Potom:
. Pro z = 0 musí být Ex = 0 pro libovolné
t.
Potom:
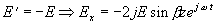 .
.
Použijeme-li vztah pro Hy
jako funkce
Ex u přímé i odražené vlny, máme
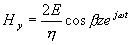 .
.
Vidíme, že z argumentu vlny
vymizela závislost na z. Zůstala jen harmonicky proměnná složka s amplitudou závislou na z. To je
stojaté vlnění, charakterizované Ex = 0 pro
z = 0 a z =
-n.l/2,
kde n =1,2,. . . Magnetické pole má pro
z = 0 maximum a další maxima u těch
z, pro které Ex
= 0. U stojaté vlny již neplatí, že v každém okamžiku a místě
nese elektrické pole stejnou energii jako magnetické pole, neboť existují místa, kde magnetické pole je
nulové, celá energie je v elektrickém poli a naopak. Střední hodnota přes periodu z
Poyntingova vektoru musí být rovna 0 v každé rovině pro z <
0. Tyto výsledky lze intuitivně zobecnit na analogii mezi přenosovým vedením a
šířením elektromagnetické vlny:
Napišme si vztahy pro Ex ,Hy,
k a h na
jedné straně a U(z), I(z),
b a zo na druhé straně:
Analogie je velmi zřejmá. Je
třeba ji ještě doplnit o analogii „okrajových“ podmínek na rozhraní dvou
materiálů (přenosových vedení s různými charakteristikami). V případě kolmého
dopadu vlny víme, že tangenciální složky elektrického i magnetického pole musí být na
rozhraní spojité a tedy Ex a
Hy musí být spojité. To
odpovídá „spojitosti“ (rovnosti) proudů a napětí na přenosovém vedení. Aby
se tato analogie dovedla do konce, je možné definovat vlnovou impedanci
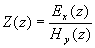 . Pro jednu vlnu šířící se ve směru kladné osy x
je tento
poměr roven h - vnitřní impedanci média, kterým se vlna šíří. Na druhé straně je h
možné nazvat charakteristickou vlnovou impedancí. Pro vlnu šířící se opačným směrem
je tento poměr roven - h.
Podobně bychom mohli napsat pro vlnovou impedanci ve vzdálenosti l od stěny, na které je vlnová impedance
rovna ZL vzorec:
. Pro jednu vlnu šířící se ve směru kladné osy x
je tento
poměr roven h - vnitřní impedanci média, kterým se vlna šíří. Na druhé straně je h
možné nazvat charakteristickou vlnovou impedancí. Pro vlnu šířící se opačným směrem
je tento poměr roven - h.
Podobně bychom mohli napsat pro vlnovou impedanci ve vzdálenosti l od stěny, na které je vlnová impedance
rovna ZL vzorec:
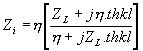 , je-li h vlnová impedance média, kterým se vlna šíří.
, je-li h vlnová impedance média, kterým se vlna šíří.
Pokud by nás překvapilo, že v případě vlny jde vlastně o odraz a ne o impedanci, je
třeba si uvědomit, že i pro vlnu můžeme definovat „nepřizpůsobení“ vzhledem k
h. Pak
je koeficient odrazu v jasném vztahu k ZL:
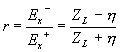 .
.
Tato analogie je velmi důležitá, neboť nám dává možnost
užití Smithova diagramu i pro případ šíření vln.
Při
dopadu elektromagnetické vlny na dielektrické rozhraní pod obecným úhlem q
(viz [3] str. 154-160) z prostředí e1,
m1
do prostředí e2, m2
platí, označíme-li úhel lomu q "
a úhel
odrazu q ' (lomené veličiny ", odražené ' ):
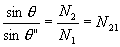 (Snellův zákon)
(Snellův zákon)
q = q '
(zákon odrazu)
Pro amplitudy E a H platí tzv.
Fresnelovy vzorce:
a) E kolmá na rovinu dopadu - tečná
složka k rozhraní se zachovává:
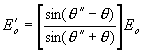
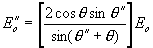
koeficient odrazu energie (časové střední hodnoty Poyntingova
vektoru):
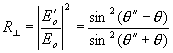
b) E rovnoběžná s rovinou dopadu -
tečná složka H se zachovává:
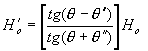
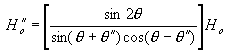
RII =
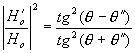
RII =
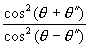
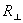
Pro vlnu dopadající pod
Brewsterovým úhlem qB
(tg qB =
N21)
platí, že RII =
¥ a tedy, že vlna je lineárně polarizovaná v rovině
kolmé k rovině dopadu. Pro
průchod z opticky hustšího do opticky řidšího prostředí (N2<
N1)
nastává pro úhly dopadu ³
qR
(sin qR =
N21) totální odraz, tím se veškerá energie odráží zpět do původního prostředí.
hlavní stránka | další >>>
![]() . Pro z = 0 musí být Ex = 0 pro libovolné
t.
Potom:
. Pro z = 0 musí být Ex = 0 pro libovolné
t.
Potom:
![]() .
. 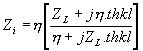 , je-li h vlnová impedance média, kterým se vlna šíří.
, je-li h vlnová impedance média, kterým se vlna šíří. 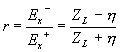 .
.