Zákonitosti platné pro stacionární elektrické a magnetické pole jsou jen podmnožinou zákonitostí platných pro časově proměnná elektrická a magnetická pole. Proto i postupy řešení elektrických obvodů s účastí zdrojů elektrického a magnetického pole, které jsou funkcí času, jsou složitější než přístupy užívané ve stacionárním případě. Názvem „vysokofrekvenční obvody“, příp. „obvody s rozloženými parametry“ se označují takové obvody, kdy vlnová délka, odpovídající časové změně elektrického a magnetického pole, je srovnatelná, případně menší než jsou rozměry příslušného obvodu. Název „vysokofrekvenční “ je někdy zavádějící, neboť i obvody pracující s poměrně nízkou frekvencí musíme řešit jako obvody s rozloženými parametry, pokud mají velké rozměry.
Pro představu:
|
f ≈ 30 GHz, λ ≈ 1 cm |
f ≈ 10 GHz, λ ≈ 3 cm |
|
f ≈ 3 GHz, λ ≈ 10 cm |
f ≈ 1 GHz, λ ≈ 30 cm |
|
f ≈ 300 MHz, λ ≈ 1 m |
f ≈ 100 MHz, λ ≈ 3 m |
|
f ≈ 30 MHz, λ ≈ 10 m |
f ≈ 10 MHz, λ ≈ 30 m |
Ale pro f ≈ 50Hz, λ ≈ 6000 km a tedy dlouhá síťová přenosová vedení je třeba uvažovat jako vedení s rozloženými parametry. Je proto důležité si uvědomit, že postupy, které budeme aplikovat, platí nejen pro obvody o rozměrech řádu desítek cm a frekvence řádu jednotek až desítek GHz, ale i pro obvody pracující s poměrně nízkými kmitočty, pokud jejich rozměry jsou příslušně veliké.
Skutečnost, že přístupy k řešení stacionárních
obvodů neplatí pro obvody s časově proměnnými veličinami, je možné
demonstrovat na I. Kirchhoffově zákoně o proudech v uzlu:
neboli, že součet
proudů do uzlu vtékajících je v každém časovém okamžiku roven nule (proudy
bereme s příslušnými znaménky - do uzlu se znaménkem minus, z uzlu se
znaménkem plus). Tento výrok je ekvivalentní výroku, že v uzlu se
nehromadí el. náboj, neboť pokud by se hromadil, musel by existovat časový interval,
kdy proud tekoucí do uzlu by se nerovnal proudu tekoucímu z uzlu.
Dokažme nyní, že obecně se v uzlu el. náboj hromadí:
Mějme rozhraní dvou homogenních vodivých látek, charakterizovaných vodivostí (σ) a permitivitou (ε). Příkladem budiž spoj měděného vodiče s vodičem z odporového materiálu. Budeme označovat veličiny vztahované k jednomu materiálu indexem 1 a ke druhému materiálu indexem 2.
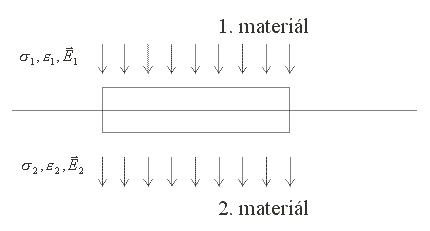
Obr.1.1.1 Rozhraní dvou homogenních látek
Přechodem protéká
proud charakterizovaný proudovou hustotou
. Vytkneme-li si v rozhraní
„pilulku“ o podstavě A a zanedbatelné výšce
tak, aby jedna podstava ležela v materiálu 1 a druhá v materiálu 2.
Pak podle Gaussovy věty musí být tok vektoru elektrické indukce roven náboji uzavřenému v objemu ohraničeném plochou, přes kterou
tok počítáme. Zde tok je
(zanedbáváme tok přes plášť pilulky, počítáme pouze podstavy).
tedy:
=>
=>
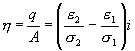
Protože 
je obecně různé
od
, je
i v případě, že rozhraním protéká proud, na rozhraní nenulový náboj.
Ten zajišťuje, aby vzniklo elektrické pole, které působí na nosiče náboje
silou a ty se pak pohybují ve směru
podle Ohmova zákona
. Protože tato plošná hustota náboje je úměrná proudu, musí
se náboj při změně proudu měnit a tak nemůže v každém okamžiku
platit: „co přiteče, to odteče“.
Podobně ani II. Kirchhoffův zákon neplatí bez úprav pro časově proměnné pole. Podle něj by například smyčkou vodiče beze zdrojů nemohl téci žádný proud. Ale víme, že pokud je smyčka součástí sekundáru transformátoru, případně je-li umístěna v poli vysílače, že proud teče - případně, pokud by byla rozpojena, že na jejich koncích vzniká rozdíl potenciálů.
Z těchto případů je vidět, že nelze obecně přenášet platnost zákonů pro stacionární elektrické a magnetické pole na nestacionární situaci. Pokud pracujeme s časově proměnnými poli, musíme se řídit zákony platnými pro takto proměnné pole. V řadě případů není přitom nutné řešit přímo Maxwellovy rovnice a je možné vypracovat jednodušší přístup (např. symbolická metoda pro řešení ustáleného stavu obvodů pracujících s harmonicky proměnným napětím a proudem).