3.3.1. Princip funkce bipolárního tranzistoru
Na obrázku 3.26.

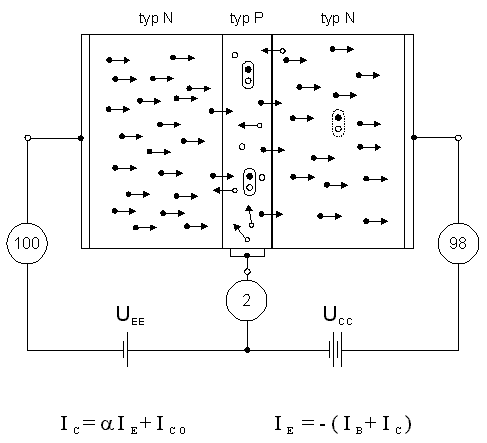
obr. 3.26
vidíme velmi zjednodušeně základní strukturu bipolárního tranzistoru. Bipolární tranzistor nazýváme tak proto, že se v jeho funkci účastní nosiče náboje obou polarit. Bipolární tranzistor se skládá ze dvou přechodů PN, které jsou odděleny je velmi tenkou vrstvou polovodiče. Podle toho, zda střední vrstva je typu P nebo typu N rozeznáváme bipolární tranzistory typu NPN nebo PNP. Co to znamená ”velmi tenká” vrstva polovodiče? Měřítkem je tzv. difuzní délka nosičů. Vstřikujeme-li např. elektrony do polovodiče typu P, vytvoříme v polovodiči typu P v blízkosti přechodu vysokou koncentraci elektronů, která bude exponenciálně ubývat v důsledku rekombinace se vzrůstající vzdáleností od přechodu a vytvářet tak gradient koncentrace, který je příčinou difuze elektronů do polovodiče typu P. Vzdálenosti, na které koncentrace ubyde na 1/e násobek původní hodnoty (zde e je základ přirozených logaritmů, e=2.7182818...), říkáme difuzní délka a je jednou z charakteristik polovodiče. Bude-li šířka střední vrstvy polovodiče malá ve srovnání s difuzní délkou, jen malá část nosičů difundujících touto částí bude rekombinovat.
Základní zapojení bipolárního tranzistoru je rovněž znázorněno na obrázku 3.26. Spočívá v tom, že jeden přechod PN je pólován v propustném směru vůči střední části a zbývající vůči téže části v závěrném směru. Vnější elektrodu tranzistoru přiléhající k přechodu pólovanému v propustném směru nazýváme emitorem (nebo emiterem), střední část bází a zbývající elektrodu kolektorem. Na obrázku 3.26. je tranzistor nakreslen zcela symetrický, takže pojmenování elektrod je odvozeno výlučně od polarity napájecích zdrojů; v praxi bývá plocha kolektoru podstatně větší, než plocha emitoru, dotace emitoru příměsemi bývá vyšší a dotace kolektoru nižší. Důvody pro to si vysvětlíme v průběhu výkladu funkce tranzistoru.
Díky pólování přechodu emitor-báze v propustném směru dochází injekci majoritních nosičů z emitoru do báze. Abychom nemuseli vždy opisovat oba případy (PNP i NPN), vybereme si k výkladu typ NPN. Elektrony jako majoritní nosiče v emitoru jsou tedy injekovány do báze a v blízkosti přechodu emitor-báze se tedy v bázi vytváří zvýšená koncentrace elektronů. Vzniká tedy gradient koncentrace elektronů v bázi tak, že směrem ke kolektorovému přechodu elektronů v bázi ubývá. Gradient koncentrace elektronů v bázi je důvodem pro difuzi elektronů skrz bázi směrem klesajícího gradientu, tedy směrem ke kolektorovému přechodu. Cestou skrz bázi řada elektronů zrekombinuje, neboť majoritními nosiči v bázi jsou díry a tedy pravděpodobnost rekombinace je vysoká, avšak vzhledem k tomu, že tloušťka báze je malá ve srovnání s difuzní délkou, velké procento elektronů se dostane do bezprostřední blízkosti přechodu báze-kolektor. Tento přechod je pólován v závěrném směru, ale pro majoritní nosiče v bázi, tedy díry. Elektrony, které prodifundovaly bází ke kolektorovému přechodu ”vidí” naopak potenciálový skok v urychlujícím směru a tak všechny elektrony, které se dostaly do blízkosti kolektorového přechodu (do oblasti dané šířkou přechodu báze-kolektor), budou tímto potenciálovým skokem vtaženy do kolektoru. Teče-li bází elektronový proud, je nutné do báze dodávat díry na rekombinaci těch elektronů, které v bázi rekombinují; tento děrový proud tedy tvoří proud báze. Vzhledem k tomu, že v bázi zrekombinuje jen malé procento z celkového proudu elektronů, je bázový proud malý ve srovnání s proudem, který teče cestou emitor-báze-kolektor. Kromě složky kolektorového proudu tvořené elektrony, které prošly bází od emitoru existuje ještě jedna složka a to závěrný proud kolektorové diody, tvořený minoritními nosiči v bázi a v kolektoru. Pro kolektorový proud můžeme tedy napsat rovnici, kterou nazýváme základní rovnicí tranzistoru
Ik = Ik0 + α Ie,
kde Ik je celkový proud kolektoru, Ik0 zbytkový proud diody báze-kolektor, α proudové zesílení tranzistoru v zapojení se společnou bází a Ie emitorový proud. Kromě této rovnice musí proudy Ik, Ib a Ie splňovat 1. Kirchhoffův zákon, tedy
Ie = Ib + Ik,
kde Ib je proud bází. Zdálo by se, že proud Ik0 bychom mohli zanedbat vzhledem ke složce od emitoru, ale nejde to, neboť jednak Ie může být rovno nule a pak Ik0 tvoří jedinou složku kolektorového proudu, jednak při překročení maximálního závěrného napětí diody kolektor-báze dojde k průrazu kolektorové diody (nemusí být nutně destruktivní) a ”zbytkový” proud Ik0 pak bude tvořit převažující složku kolektorového proudu. Koeficient proudového zesílení tranzistoru v zapojení se společnou bází, α, je paradoxně menší než jedna, ale z popisu principu funkce již víte, proč tomu tak je a navíc budeme ještě definovat koeficient proudového zesílení v zapojení se společným emitorem, β, a ten už větší než jedna bude. Koeficient α má standardně hodnoty okolo 0,99 u běžných ”dobrých” křemíkových tranzistorů, ale může dosáhnout i hodnoty okolo 0,999. Podle čeho rozeznáváme zapojení se společným emitorem, kolektorem a bází? Podle toho, která elektroda je společná ”budicímu” a výstupnímu obvodu; na obrázku 3.26. je to báze. Uveďme si nyní schematické značky tranzistoru podle obrázku 3.27.
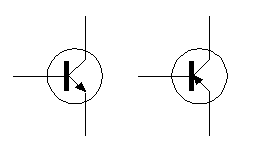
obr. 3.27
Typy PNP (vpravo) a NPN
(vlevo) se rozlišují směrem šipky u emitoru. Mnohdy
konstruktéři nekreslí kroužek znázorňující schematicky
pouzdro tranzistoru, tak se tím nenechte zmást; na funkci bipolárního
tranzistoru se tím nic nemění.
Podívejme se nyní na zapojení se společným emitorem, je na
obrázku 3.28. Na tomto obrázku je zakreslen jednostupňový
tranzistorový zesilovač se společným emitorem.
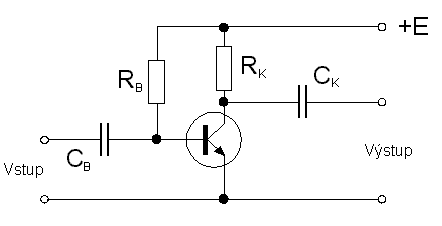
obr. 3.28
Budicím obvodem je, obdobně jako v případě zapojení se společnou bází, obvod báze-emitor, výstupním obvodem je ale obvod kolektor-báze-emitor. Budicím proudem je proud do báze, Ib, výstupním proudem proud kolektoru, Ik. Po relativně snadné transformaci soustavy dvou rovnic uvedených v předchozím odstavci (základní rovnice tranzistoru a Kirchhoffův zákon), vyjde nám analogie základní rovnice tranzistoru pro zapojení se společným emitorem:
Ik = (α/(1-α))Ib + (1/(1-α))Ik0 = βIb + Ik0’
a Kirchhoffův zákon platí ve stejné podobě jako pro zapojení se společnou bází,
Ie = Ib + Ik.
Zde jsme označili
β = α/(1-α)
a Ik0’ = Ik0 / (1-α) = (β+1)Ik0.
Koeficient β nazýváme proudové zesílení tranzistoru v zapojení se společným emitorem a Ik0’ zbytkovým proudem tranzistoru v zapojení se společným emitorem. V katalogu je obvykle uváděn koeficient β a Ik0; důvody pro to jsou spíše obchodní než fyzikální. V katalogu se rovněž můžete setkat s označením h21b místo α a h21e místo β, souvisí to s náhradním zapojením tranzistoru, tzv. hybridním náhradním zapojením, ale tím se v tomto učebním textu nebudeme zabývat. Vidíme tedy, že zapojením tranzistoru se společným emitorem jsme získali velký koeficient proudového zesílení
β = α/(1-α),
ale zároveň jsme obdrželi podstatně větší zbytkový proud kolektoru,
Ik0’=(β+1)Ik0.
Ukažme si ještě jednu ”nectnost” zapojení se společným emitorem a tou je nižší tzv. mezní frekvence tranzistoru. K pojmu mezní frekvence nebo mezního kmitočtu tranzistoru dospějeme nejprve pro zapojení se společnou bází podle obrázku 3.29.,
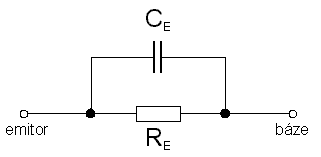
obr. 3.29
na kterém jsme si nahradili emitorový přechod tranzistoru paralelní kombinací odporu Re a kapacity Ce. Při diskusi o diodách s přechodem PN jsme si již ukázali, že kapacita přechodu je jeho inherentní vlastnost a není tedy možné vyrobit PN přechod s kapacitou rovnou nule. Proud Ie tekoucí do této kombinace zleva nám představuje proud, kterým v zapojení se společnou bází budíme tranzistor. Pouze složka Ier, která prochází rezistorem, představujícím činnou složku impedance emitorového přechodu bude tranzistorem zesílena, složka Iec, která prochází větví s kapacitou, zesílena nebude. Vyjádřeme si poměr Ier/Ie; ten nám bude představovat závislost koeficientu proudového zesílení v zapojení se společnou bází, α, na kmitočtu. Jest totiž, jak jsme konstatovali, koeficient α dán poměrem změny kolektorového proudu, dIk ke změně emitorového proudu, dIe, tj.
α = dIk / dIe = (dIk / dIer)·(dIer / dIe).
Snadnou manipulací dojdeme ke vztahu, že
Ier/Ie = (1+jω/ω0)-1,
kde jsme označili ω0=ReCe. Poměr Ier/Ie je nezávislý na Ie a je tedy
Ier / Ie = dIer / dIe.
Kmitočtu ω0 = 2πf0 říkáme mezní kmitočet tranzistoru v zapojení se společnou bází. Můžeme tedy pro zapojení se společnou bází napsat pro frekvenční závislost koeficientu proudového zesílení α=α0/(1+jω/ω0), kde jsme označili symbolem α0 koeficient proudového zesílení tranzistoru se společnou bází pro frekvenci ω=0. Výraz pro frekvenční závislost α připomíná výraz pro napěťový přenos integračního filtru RC. Připomeňme si průběh amplitudy a fáze tohoto výrazu. Absolutní hodnotu neboli amplitudu komplexního čísla dostaneme podle Pythagorovy věty jako odmocninu ze součtu kvadrátů reálné a imaginární složky. Snadnými úpravami dospějeme k výrazu
α = α0 ( 1 + (ω/ω0)2)-1/2, tg φ = -ω /ω0,
kde jsme si symbolem φ označili fázi. Pro nízké kmitočty je α asymp; alpha;0 a fáze φ≈0 (radiánů). Pro ω=ω0 je α = α0/2 a φ=π/4. Pro vysoké kmitočty klesá α jako
α ≈ α0ω0/ω a fáze φ → -π/2.
O α říkáme, že klesá se sklonem 20 dB na dekádu, nebo, což je totéž, se sklonem 6 dB na oktávu. Připomenu ještě decibel, dB. Bezrozměrné číslo A, vyjadřující např. zesílení zesilovače, poměr dvou napětí, útlum apod., vyjádříme v decibelech jako
A [dB] = 20 log10A.
Je-li tedy A=10, je to v decibelech 20, je-li A=100, je to v decibelech 40, je-li A=2, je to v decibelech (zhruba) 6. Frekvenční závislosti veličin znázorňujeme nejčastěji v grafu log-log a reálné křivky nahrazujeme jejich tečnami; zvýrazní se tak význam bodů ”zlomu” frekvenčních závislostí, neboť se dá ukázat, že tečny v měřítku log-log se právě protínají v bodech, jejichž souřadnice na ose ω je dána právě převrácenou hodnotou odpovídající časové konstanty RC. Těmto grafům říkáme Bodeho diagramy (anglicky Bode plot) a Bodeho diagram pro náš případ frekvenční závislosti α je uveden na obrázku 3.30.
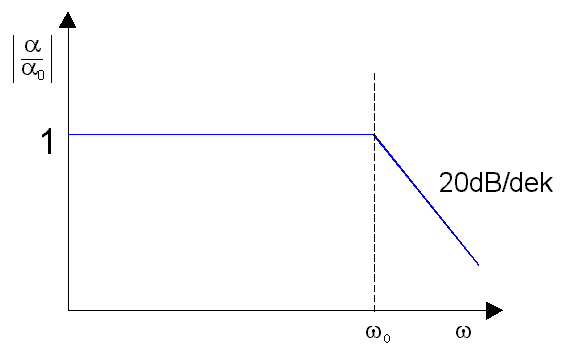
obr. 3.30
Vyjádřeme si nyní frekvenční závislost β použitím odvozené závislosti pro α a vztahu
β = α / (1-α).
Po nepříliš složité úpravě výrazu dojdeme ke vztahu
β = β0 / (1+jω/ω0’), kde β0 = α0/(1-α0) a ω0’=(1-α0)ω0.
Frekvenci ω0’ říkáme mezní kmitočet tranzistoru v zapojení se společným emitorem. Zde vidíme, že mezní kmitočet tranzistoru je v zapojení se společným emitorem značně nižší, než v zapojení se společnou bází. Například pro α0=0,99 je ω0’ jen 1% z ω0.