3.1.3. Příměsové polovodiče

Význam polovodičů, zejména křemíku, pro výrobu polovodičových součástek vynikne až popisem tzv. příměsových polovodičů, tj. polovodičů, do kterých byla přidána určitá koncentrace příměsí. Vzhledem k tomu, že křemík je čtyřmocný prvek, používají se příměsi třímocné a pětimocné. Kvalitativní popis funkce příměsí v křemíku je následující.

Umístíme-li do krystalové mřížky křemíku pětimocný prvek, bude pátý valenční elektron příměsi daleko slaběji vázán a bude tedy mít velkou pravděpodobnost delokalizace, tj. odtržení od mateřského atomu, a bude pak přispívat k vedení proudu. Na místě původního atomu příměsi pak zbyde kladný, jednou nabitý, iont. Prakticky každý atom příměsi tak přispěje k celkové koncentraci volných nosičů jedním elektronem a protože vlastní koncentrace nosičů v křemíku je velmi malá (zhruba na každých 5·10¹² atomů jediný volný elektron a díra) stačí velice malá koncentrace příměsí k tomu, aby podstatně zvýšila koncentraci elektronů (nikoliv děr). Např. koncentrace příměsí 1 ppm, tj. 10^-6, zvýší koncentraci elektronů na cca 5·10²² m^-3, tedy o 6 řádů. Příměsi v tomto případě nazýváme příměsi typu n nebo donory, neboť odevzdávají elektron. Elektrony, jejichž koncentrace vzrostla, nazýváme majoritními nosiči, díry minoritními nosiči. Takto dotovanému (termín pro polovodič obohacený příměsemi) polovodiči říkáme polovodič typu n.

Bude-li v krystalové mříži třímocný atom, bude mít značnou schopnost vázat na sebe jeden elektron (jak uvidíme z pásového diagramu, elektron z valenčního pásu) a tím uvolnit jednu díru ve valenčním pásu. Na místě atomu příměsi pak bude vázaný záporný iont (opět jednou nabitý) příměsi. Opět stačí velmi malá koncentrace příměsi k tomu, aby postatně ovlivnila koncentraci nosičů, tentokrát děr. Příměsi v tomto případě nazýváme příměsi typu p nebo akceptory, neboť přijímají jeden elektron, díry, jejichž koncentrace vzrostla, majoriními nosiči, elektrony minoritními nosiči. Takto dotovanému polovodiči říkáme polovodič typu p.

Dá se ukázat, že v obou případech zůstává součin n.p konstantní, nezávislý na koncentraci příměsí, tj. kolikrát zvýšíme koncentraci elektronů tolikrát snížíme koncentraci děr v případě pětimocné příměsi a v případě třímocné příměsi můžeme formulovat duální obdobu tohoto výroku. Bystrou čtenářku jistě nyní napadne otázka (není vyloučeno, že tato otázka napadne i bystrého čtenáře), proč je tomu tak, že se zvýšením koncentrace nosičů jednoho druhu snížíme koncentraci nosičů druhého druhu? A bystrou čtenářku vzápětí napadne další otázka: jak to, že když termální excitace elektronů stále ”zásobuje” vodivostní pás elektrony, že nedojde k jeho ”přeplnění”? Odpověď na obě otázky je ve fyzikálním efektu, který jsme dosud nezmínili, a tím je tzv. rekombinace. Existuje-li elektron ve vyšším energetickém stavu ve vodivostním pásu, může se snadno stát, že např. při srážce s atomem v mřížce dojde k předání takové energie, že elektron ”spadne” z vodivostního do valenčního pásu, čímž zároveň ”zlikviduje” jednu díru. Hovoříme o rekombinaci páru elektron-díra. Je zřejmé, že pravděpodobnost rekombinace roste s koncentrací buď jednoho nebo druhého nebo obou druhů nosičů a naopak. Je tedy zřejmé, že v případě příměsových polovodičů, kdy koncentrace majoritních nosičů je podstatně větší než koncentrace minoritních nosičů, bude z hlediska rekombinace hrát rozhodující roli koncentrace minoritních nosičů, neboť jak již bylo uvedeno, rekombinace probíhá v párech a není-li druhého do páru, nemůže rekombinace proběhnout. Teď je již jistě, alespoň kvalitativně jasné, proč klesne koncentrace děr při zvýšení koncentrace elektronů a proč se dosáhne rovnovážné koncentrace elektronů ve vodivostním pásu přestože termická generace probíhá neustále; je to dáno procesem rekombinace, který je závislý na koncentraci nosičů obojího druhu.

Abychom si poněkud přesněji popsali proces rekombinace uvažujme polovodič typu n, který po krátkou dobu ozáříme světlem vhodné vlnové délky tak, aby energie fotonů stačila na excitaci elektronů do vodivostního pásu (hovoříme o tzv. vnitřním fotoefektu, elektronické prvky na něm založené probereme později). Budeme sledovat, co se bude dít s koncentrací děr v závislosti na čase. Obecně můžeme napsat rovnici dp/dt=g-r, kde g je rychlost generace a r rychlost rekombinace. Bývá zvykem rychlost rekombinace vyjadřovat pomocí tzv. doby života τ_p tak, že poměr dt/τ_p vyjadřuje pravděpodobnost rekombinace díry za čas dt. Rychlost rekombinace bude pak dána poměrem r = p/τ_p za předpokladu, že máme dostatek elektronů se kterými mohou díry rekombinovat, tj. za předpokladu p<<n, což je v příměsovém polovodiči prakticky vždycky splněno. Pro časový průběh koncentrace děr pak máme dp/dt=g-p/&tau_p. Je-li bez ozáření koncentrace děr p_o a rychlost generace g_o = p_o/τ_p, dostáváme pro průběh koncentrace děr při zapnutí záření v čase t=0 (diferenciální rovnice je obdobná rovnici nabíjení kondenzátoru přes odpor; vzpomeňte si na přednášku z elektřiny a magnetismu)

Δp = p - p_o = (g-g_o) τ_p ( 1 - exp(-t/τ_p) ),

neboli, že koncentrace děr narůstá s časovou konstantou τ_p z hodnoty p_o na hodnotu p. Po vypnutí záření bychom dostali obdobnou závislost pro relaxaci koncentrace p na původní hodnotu p_o,

Δp = (Δp)_o exp(-t/τ_p).

V polovodičích jsou hodnoty τ_p v řádu 10^-6-10^-8 s. Tato situace je znázorněna na obr. 3.9a,b.

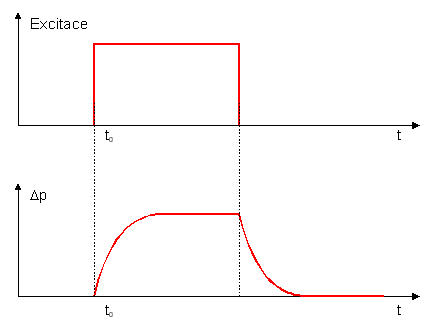
Obr. 3.9a,b

Vzájemná rekombinace elektronů a děr má ještě jeden, pro technologii výroby polovodičových prvků naprosto rozhodující výsledek: Dotujeme-li příměsový polovodič příměsemi opačné vodivosti, zvyšujeme pravděpodobnost rekombinace tím, že zvyšujeme koncentraci nosičů opačné polarity (úvaha v předchozím odstavci pak neplatí, neboť neplatí předpoklad velikého rozdílu koncentrací p a n). Dříve nebo později tedy musíme dospět do situace, že koncentrace původně majoritních nosičů bude stejně velká jako vlastní koncentrace a tedy polovodič bude mít vlastnosti charakteristické pro vlastní, intrinsický polovodič. Pokračujeme-li v dotaci, změníme postupně polovodič jedné vodivosti na polovodič opačného typu vodivosti.

Při popisu příměsových polovodičů pomocí pásových diagramů je výhodné zavést pojem tzv. příměsových hladin, tj. energetických úrovní odpovídajících hladinám příměsí. Jestliže např. je zapotřebí energie E_d’ k tomu, abychom ”utrhli” elektron od atomu příměsi (tato energie je daná jen kombinací polovodič-příměs), pak tzv. donorová hladina bude ležet o E_d’ pod spodní hranicí vodivostního pásu a podobně potřebujeme-li dodat energii E_p’, abychom ”nalepili” elektron na akceptorový atom (tj. vytvořili díru ve valenčním pásu), bude tzv. akceptorová hladina ležet o E_p’ nad horní hranicí valenčního pásu. V dalším budeme uvažovat polovodič s koncentrací donorů N_d a koncentrací akceptorů N_a tak, že např. se bude jednat o polovodič typu n, tj. N_d >> N_a. Energie E_d’ a E_a’ jsou pro křemík řádu 50 meV, tedy velmi srovnatelné s tepelnou energií elektronů při pokojové teplotě (cca 28 meV). Většina donorů i akceptorů bude pak tepelně ionizována, budou však existovat neionizované (neutrální) zbytky, jejichž koncentraci označíme po řadě N_dn a N_an. Podle zákona zachování náboje musí celkový náboj v látce zůstat nulový, tedy i v jednotce objemu, tj.

p + (N_d - N_dn) = n + (N_a - N_an),

přičemž z našeho původního předpokladu, že se jedná o polovodič typu n plyne, že N_d-N_dn >> N_a-N_an a n>>p. Tedy n ≈ N_d - N_dn. Vypočítejme si nyní polohu Fermiho meze v příměsovém polovodiči. Začneme tím, že si určíme koncentraci neionizovaných donorů z Fermi-Diracovy rozdělovací funkce. Pravděpodobnost, že donory zůstanou neionizovány je rovna pravděpodobnosti, že donorová hladina E_d = E_c-E_d’ bude obsazena elektronem a tedy

N_dn = N_d · P_FD(E_d).

Obsazení energetické hladiny s energií E_d je dáno Fermi-Diracovou funkcí bez integrace, neboť se jedná o jednu hladinu (nikoliv energetický interval).

n/N_d = 1-N_dn/N_d = 1-[1+exp(E_d-E_F)/kT]^-1.

Pro nízké teploty je zřejmě koncentrace n ve vodivostním pásu téměř nula a to je možné jedině tehdy, když exponentu zanedbáme vůči 1, tj. když E_F>E_d. Pak můžeme předpokládat, že E_F-E_d >> kT a tedy, že exponent exponenciály je velký a záporný. Zlomek rozvedeme podle vzorce (1+a)^-1 ≈ 1-a, pokud a << 1. Dostaneme (po zrušení jedniček)

n ≈ N_d exp[ -(E_d-E_F) / kT ].

Tutéž koncentraci n bychom měli dostat ze vztahu (již uvedeného)

n = (1/4) (8πm_e^∗·kT/h²)^3/2 · exp[-(E_c-E_F)/kT ] = N_c · exp[ -(E_c-E_F) / kT],

kde jsme si označili N_c = (1/4)(8πm_e^∗·kT/h²)^3/2. Logaritmováním rovnice

N_d exp[-(E_d-E_F)/kT] = N_c exp[-(E_c-E_F)/kT]

dostáváme kT·ln(N_d/N_c) = 2E_F - E_c - E_d a z toho pro

E_F = (1/2) (E_c + E_d) + (1/2)kT·ln(N_d/N_c).

Veličina N_c (fyzikálně je to efektivní hustota možných stavů elektronu ve vodivostním pásu) má hodnotu pro křemík a 300K 3,5·10²⁵ m^-3, je tedy (pro rozumné koncentrace příměsí, křemík má cca 5·10²⁸ atomů na m³) větší než N_d a argument logaritmu je menší než jedna; z toho plyne, že pro zvyšující se teplotu hodnota E_F klesá. Při nízkých teplotách leží tedy Fermiho hladina uprostřed mezi donorovou hladinou a spodní hranicí vodivostního pásu, při zvyšování teploty klesá směrem ke středu zakázaného pásu, kam by se přiblížila při nekonečně vysoké teplotě. Pro pokojové teploty můžeme předpokládat, že Fermiho hladina (opět pro rozumné koncentrace příměsí) je někde mezi středem zakázaného pásu a donorovou hladinou. Je dobré si všimnout, že při extrémně vysokých koncentracích příměsí je závislost Fermiho energie na teplotě rostoucí a je tedy možné, aby při pokojové teplotě ležela Fermiho hladina v tomto případě nad spodní hranicí vodivostního pásu (viz níže diskusi o tunelové diodě). Takovému polovodiči říkáme degenerovaný, neboť vykazuje z hlediska vodivosti vlastnosti kovu.

Naprosto stejnou úvahu a výpočet můžeme provést pro dotaci příměsemi typu p. V polovodiči nepříliš dotovaném příměsemi typu p bude tedy Fermiho hladina ležet mezi středem zakázaného pásu a akceptorovou hladinou. Pásové diagramy pro oba případy vidíme na obr.3.10 pro polovodič typu n a na obr. 3.11 pro polovodič typu p.

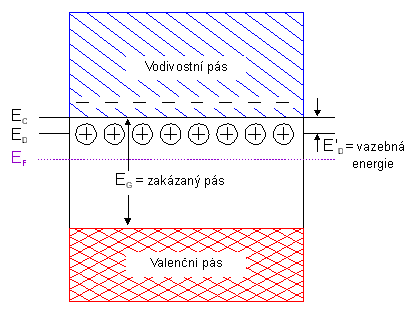
obr. 3.10

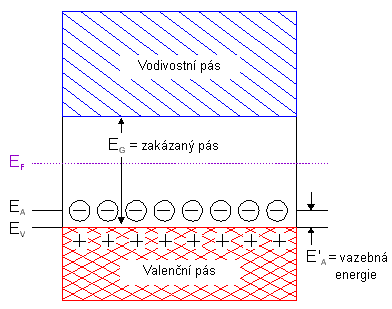
obr. 3.11

PN přechod