Základní pojmy obvodové elektroniky
Tato kapitola vymezuje základní pojmy obvodové elektroniky užívané v tomto učebním textu. Obvykle jsou tyto pojmy definovány v rámci přednášky Elektřina a magnetismus a proto, jsou-li vám známy, můžete tuto kapitolu přeskočit. Osobně doporučuji kapitolu projít a přesvědčit se, zda to, co si pod uvedenými pojmy představujete, souhlasí s tímto textem.
Ve skriptech je užita výhradně soustava jednotek SI. Z definic základních jednotek připomenu pouze ampér (A), který je definován na základě silových účinků mezi dvěma rovnoběžnými vodiči, umístěnými ve vakuu ve vzdálenosti od sebe 1 metr, kterými protéká stejný proud. Tento proud je roven 1A právě když vodiče na sebe působí silou 2.10-7 N na každý metr délky.
V řadě případů je ampér příliš velkou jednotkou a proto se užívají jeho zlomky, zavedené v řadě po násobení 10-3: mA=10-3A,µA=10-6A, nA(nanoampér)=10-9A, pA(picoampér)=10-12A, fA(femtoampér)=10-15A. Další standardně zavedená předpona je atto=10-18, v běžné praxi se s ní však nesetkáte. Z násobků ampéru lze uvést kA=103A, který se používá při popisu proudového odběru u velkých motorů, pecí, při rozvodu elektrické energie apod. Připomeňme ještě, že konvenční směr proudu ve vodiči je, na základě úmluvy, definován jako směr opačný ke směru, jakým se ve vodiči pohybují nosiče náboje, tj. elektrony.
Další jednotky užívané v elektronické praxi jsou odvozené. Není možné připomenout všechny, takže jen ty nejdůležitější. Coulomb (C) je jednotkou elektrického náboje a je definován jako ampérsekunda, A.s. Elektrický proud je tedy náboj, který proteče průřezem vodiče za jednotku času, tedy i [A] = dq [C] / dt [s] (rozměr derivace se rovná podílu rozměrů). Volt (V) je jednotkou napětí neboli rozdílu potenciálů. Je definován jako práce vykonaná přenesením jednotkového náboje v elektrickém poli, tedy mezi dvěma místy v elektrickém poli je rozdíl potenciálů 1V právě když při přenesení náboje mezi těmito místy vykonáme práci 1J. K tomu je zapotřebí vědět, že elektrické pole je pole konzervativní a že tedy tato práce nezávisí na dráze, po které náboj přenášíme. Z toho plyne převodní vztah mezi voltem a základními jednotkami, V=J/C=kg.m2.A-1.s-3. Je-li mezi dvěma body obvodu potenciálový rozdíl U, pak náboj q koná práci qU, pokud se pohybuje z místa vyššího do místa nižšího potenciálu. Ve zdroji, jakým je např. baterie nebo generátor v elektrárně, se elektrickému náboji práce dodává, když se náboj pohybuje od svorky zdroje s nižším potenciálem ke svorce zdroje s vyšším potenciálem. Potenciálový rozdíl mezi svorkami zdroje, který nedodává proud, se nazývá elektromotorická síla (ems, v angličtině emf, electromotori c force).
Okamžitý elektrický výkon na součástce elektrického obvodu je definován jako součin okamžitého napětí a okamžitého proudu (okamžité veličiny značíme malými písmeny), p = u.i. Základem této definice je experimentální pozorování nebo následující úvaha: Předpokládejme homogenní vodič (například válcového tvaru) délky x, na který připojíme napětí u. Vlivem elektrického pole dojde k pohybu nosičů náboje ve vodiči, neboť na nosiče náboje ve vodiči bude působit elektrické pole e = u/x silou f = q.e, kde q je celkový náboj prošlý průřezem vodiče za čas t, q=i.t. Pohybující se nosiče náboje ve vodiči konají práci tím, že při srážkách s atomy v mříži předávají část své energie. Vykonaná práce je
a = f.x = q.e.x = i.t.e.x = i.t.u.
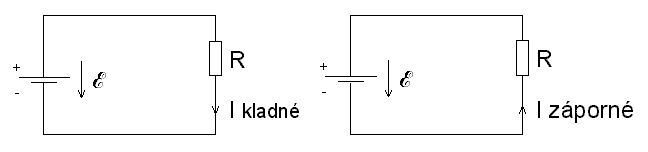
Práci vykonanou za jednotku času nazýváme výkonem, p = a/t = i.u. (Tato úvaha je rovněž založena na experimentálním pozorování, a sice na tom, že síla f působící na náboj q v elektrickém poli e je rovna f=q.e.) Jednotkou výkonu je Watt (W). Abychom mohli rozlišovat znaménko proudu, který teče v elektrickém obvodu, zavedeme následující znaménkovou konvenci, viz obrázek 1.1.

obr. 1.1
Potenciálový rozdíl mezi dvěma místy elektrického obvodu budeme značit orientovanou šipkou, směřující od místa s vyšším potenciálem k místu s nižším potenciálem. Proud protékající obvodem budeme rovněž značit orientovanou šipkou s tím, že mezi dvěma body obvodu, mezi kterými nedochází k rozvětvení, musí proud zachovat svůj směr; jinak je jeho orientace libovolná. Zavedený okamžitý výkon budeme brát s kladným znaménkem, pokud mezi dvěma místy obvodu, kde výkon počítáme, bude souhlasit orientace šipek proudu a napětí, jinak bude mít znaménko záporné. Pro případ, že se jedná o čistě odporovou zátěž můžeme též, s použitím Ohmova zákona napsat pro okamžitý výkon vztahy p=u.i=i2.R=u2/R.V případě střídavého proudu můžeme tyto rovnice aplikovat v každém časovém okamžiku.
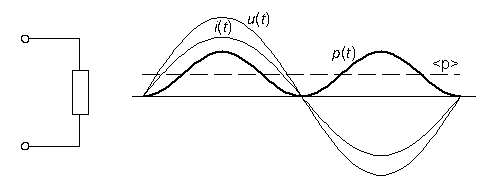
obr. 1.2
Obrázek 1.2. ukazuje průběh okamžitého napětí, proudu a okamžitého výkonu na rezistoru s odporem R. Je vidět, že okamžitý výkon má střední hodnotu nenulovou a že se mění od 0 do hodnoty um.im, kde um a im jsou amplitudy napětí a proudu na rezistoru.Pro pojem okamžitého výkonu neexistuje žádné praktické využití, co nás v praxi skutečně zajímá je střední výkon, který budeme značit P. P je tedy časová střední hodnota okamžitého výkonu, P = <p> = <i2>.R = <u2>/R. Je velmi důležité si uvědomit, že kvadrát střední hodnoty veličiny je něco úplně jiného než střední hodnota kvadrátu této veličiny. V našem případě střední hodnota kvadrátu je nenulová, kladná (na obrázku 1.2. naznačena čárkovaně), kvadrát střední hodnoty (pro střídavý průběh napětí a proudu) je nula.
S pojmem středního výkonu jsou spojeny pojmy efektivní hodnoty proudu a napětí. To jsou například hodnoty udávané v elektrickém rozvodu, tedy např hodnota napětí 220V v zásuvce je hodnota efektivní, nikoli maximální, okamžitá nebo střední. Efektivní hodnoty jsou definovány jako odmocniny ze středních hodnot kvadrátu veličiny. (Jistě znáte definici efektivní hodnoty přes tepelné účinky jako takovou hodnotu stejnosměrné veličiny,která má stejné tepelné účinky jako střídavá veličina; tyto dvě definice jsou totožné, přesvědčte se o tom.) Tedy
Ief = (<i2>)1/2, uef = (<u2>)1/2.
Protože platí, že u=R.i, platí jistě také, že u2=i2R2 a tedy, že <u2>=<i2>.R2. Odmocníme-li, dostaneme vztah Uef=IefR. Protože jistě platí, že
<u2> = Uef Uef a <i2> = Ief Ief,
platí také, že
P = <u2> / R = Uef Uef / R = Uef Ief.
(Stejný výsledek bychom dostali ze vztahu P = <i2>R) Efektivní hodnoty jsou tedy proto tak užitečné, že z hlediska výkonu s nimi můžeme pro střídavé průběhy počítat jako kdyby se jednalo o stejnosměrné veličiny.
V případě, že napájíme střídavým proudem ideální indukčnost L (tedy indukčnost, která nezávisí na protékajícím proudu a která je vytvořena z vodiče o nulovém odporu), se energie dodávaná zdrojem nedisipuje, ale periodicky shromažďuje v indukčnosti a vydává do obvodu. Okamžitý výkon má střídavý průběh a jeho střední hodnota je tedy rovna nule. Průběh napětí na indukčnosti, kterou protéká střídavý proud, je znázorněn na obrázku 1.3. spolu s průběhem okamžitého výkonu. Na obrázku 1.4. je průběh proudu, okamžitého výkonu a okamžité energie magnetického pole nashromážděné v indukčnosti w=1/2.Li2.
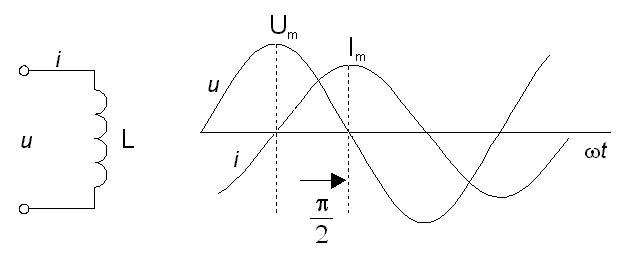
obr. 1.3
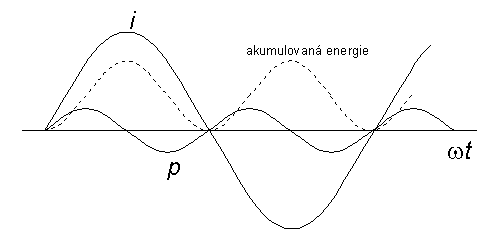
obr. 1.4
Zde je nutné upozornit na to, že ideální indukčnost neexistuje, má vždy nenulový odpor, na kterém se disipuje energie a je-li vybavena feromagnetickým jádrem, je indukčnost nelineární funkcí protékajícího proudu (může nastat magnetická saturace) a vlivem hystereze (ta nastává jako důsledek přemagnetovávání magnetických domén ve feromagnetickém materiálu) vznikají další ztráty energie spojené s tímto efektem.
V případě kondenzátoru připojeného na střídavé napětí jím protéká proud daný vztahem i=C.du/dt. Obdobně jako v případě indukčnosti má okamžitý výkon střídavý průběh a jeho střední hodnota je tedy rovná nule. Okamžitá energie elektrického pole v kondenzátoru je rovna w=1/2.C.u2. V průběhu periody střídavého napětí tato nashromážděná energie mění svoji velikost od nuly do maximální hodnoty. Obrázek 1.5. znázorňuje průběhy napětí, proudu, okamžitého výkonu a okamžité energie elektrostatického pole v kondenzátoru v závislosti na čase pro několik period střídavého průběhu.
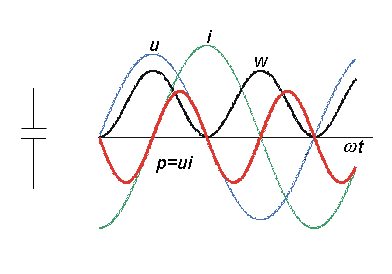
obr. 1.5
U ideálního kondenzátoru a ideální cívky je fázový úhel φ mezi proudem a napětím roven ±π/2 (u kondenzátoru se napětí zpožďuje za proudem, u cívky se proud zpožďuje za napětím). Aplikujeme-li střídavý proud nebo střídavé napětí na obecnou impedanci, může fázový úhel mezi napětím a proudem nabýt libovolné hodnoty mezi -π/2 a +π/2. Označíme-li tento fázový úhel φ, můžeme napsat pro okamžité hodnoty proudu, napětí a výkonu:
i = Im cos(ωt),
u = Um cos(ωt+φ),
p = u i = Um Im cos(ωt+φ) cos(ωt).
Na obrázku 1.6. je znázorněn jeden specifický případ, kdy se proud opožďuje za napětím o úhel o něco menší než je π/2. Říkáme, že taková impedance má induktivní charakter, byla by nejspíše složena ze sériové kombinace rezistoru a cívky. Přestože obrázek je kreslen pro tento případ (jinak to v zájmu přehlednosti ani nejde), naše další úvahy platí pro libovolný fázový úhel φ. Použitím trigonometrické identity
cos(x) cos(y) = 1/2 [ cos(x-y) + cos(x+y) ]
dostáváme pro okamžitý výkon vztah
p = 1/2 Um Im [ cos(φ) + cos(2ωt+φ) ].
Budeme-li počítat střední hodnotu p přes jednu periodu, bude se tato sestávat ze součtu středních hodnot obou sčítanců. Časová střední hodnota druhého sčítance je však rovna nule, takže dostáváme
P = <p> = 1/2 Um Im cos(φ) = Uef Ief cos(φ).
Jak vidno, používali jsme řadu trigonometrických identit (včetně vztahu (Uef)2 = (Um)2/2, takže odvozený výsledek platí pouze pro harmonický průběh napětí a proudu. Výrazu cos(φ) se říká účiník (anglicky power factor). Odvozený vztah platí i pro čistě induktivní nebo čistě kapacitní zátěž, kde jest φ=±π/2 a tedy P=0. V případě, že se impedance zátěže blíží čisté indukčnosti nebo čisté kapacitě, je reálný výkon malý přesto, že přívodními vodiči mohou téci velké proudy. Je to proto, že v případě, že zátěž není čistě ohmická, vytváříme periodicky energii v magnetickém nebo elektrickém poli a tato energie se do obvodu opět vrací ve vhodné části periody. Proto nazýváme výkon P skutečným výkonem (anglicky active power). Na druhé straně můžeme definovat část výkonu, která se pouze používá na vytváření energie v cívkách, eventuálně kondenzátorech obvodu. Říkáme jí jalový výkon (anglicky reactive power) a značíme Q. Jalový výkon je definován jako Q = Uef Ief sin(φ), kde φ má již definovaný význam zpoždění proudu za napětím. Na uvedené definice skutečného a jalového výkonu lze též nahlížet podle obrázku 1.7.
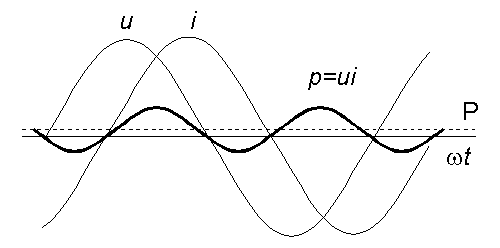
obr. 1.6
Zde máme nakresleny fázory napětí a proudu, které svírají mezi sebou úhel φ. Fázory napětí a proudu budeme značit U a I (není nutné zavádět pro komplexní veličiny jiná označení, pracujeme prostě s nimi jako s komplexními čísly, jsou-li to reálné veličiny, tím lépe). Velikosti těchto fázorů jsou po řadě Uef a Ief. Projekce napětí do směru proudu je Uef.cos(φ), projekce proudu do směru napětí je Ief cos(φ). Skutečný výkon je tedy dán součinem proudu a napětí, které jsou ve fázi. Naopak projekce napětí do směru kolmého ke směru proudu je Uef sin(φ) a rovněž projekce proudu do směru kolmého k napětí je Ief sin(φ). Jalový výkon je tedy dán součinem proudu a napětí, které mají navzájem fázový posun ±π/2. Na skutečný a jalový výkon se můžeme formálně dívat jako na složky fázoru v komplexní rovině, viz obrázek 1.8.
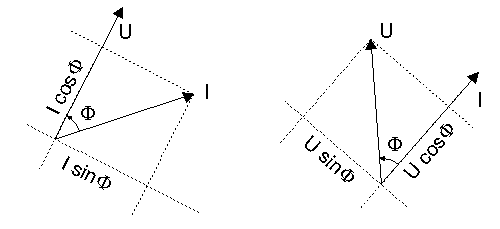
obr. 1.7
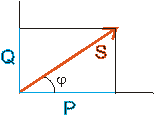
obr. 1.8
Definujeme pak komplexní výkon
S = P + jQ = Uef Ief [ cos(φ) + j sin(φ) ].
Je zřejmé, že velikost S je rovna Uef Ief a říkáme jí zdánlivý výkon. Komplexní výkon lze vyjádřit ještě jedním vztahem, uvědomíme-li si, že fázor proudu I je vlastně komplexní číslo a existuje tedy k němu číslo komplexně sdružené (geometricky je to fázor s opačným znaménkem fázového úhlu) I*. Pak můžeme pro komplexní výkon napsat S=U·I*. Důkaz je jednoduchý, napíšeme si prostě fázory napětí a proudu ve tvaru komplexní exponenciály:
U = Uef exp[ j(ωt+φ)], I = Ief exp(jωt).
I* je pak Ief exp(-jωt) a tedy S = U·I* = Uef Ief exp(jφ), c.b.d. K procvičení se v operacích s komplexními čísly dokažte (pro teoretickou práci někdy užitečné) vztahy
P = 1/2·(U I* + U* I), Q = 1/2·(U I* - U* I).
Vyjádříme-li si impedanci Z na které výkon počítáme jako
Z = U / I = (Uef/Ief) exp(jφ) a Z = R + j X,
můžeme pro komplexní výkon napsat S = Uef Ief exp(jφ) = Ief2 (Uef/Ief) exp(jφ) = Ief2 Z = Ief2 R + j Ief2 X.
Je tedy (S = P + j Q), P = Ief2 R a Q = Ief2 X. Tyto vztahy nám říkají, že odporová složka zátěže spotřebovává skutečný výkon, imaginární složka zátěže (induktance, kapacitance, je-li jaká) spotřebovává jalový výkon. Přitom induktance spotřebovává kladný jalový výkon, kapacitance záporný jalový výkon. Pokud máme připojeny dvě zátěže, jednu induktivního a druhou kapacitního charakteru, obě zátěže dohromady budou spotřebovávat jen rozdíl mezi oběma jalovými výkony. To je princip kompenzace účiníku. Převažuje-li například v továrně induktivní zátěž elektrických motorů, zapojuje se paralelně k zátěži motorů kapacitní zátež, aby došlo ke kompenzaci spotřebovaného jalového výkonu. Místo formulace "kapacitní zátěž spotřebovává záporný jalový výkon" můžeme říkat, že kapacitní zátěž vytváří kladný jalový výkon. Vzhledem k tomu, že fyzikální podstata jalového výkonu je vlastně akumulace energie v magnetickém nebo elektrickém poli, musí platit (odobně jako platí pro skutečný výkon) zákon zachování jalového výkonu, tedy kolik jalového výkonu se v systému produkuje, tolik se jej musí spotřebovat. Nakonec jednotky. Skutečný výkon Watt, W, kilowatt, kW, megawatt, MW. Jalový výkon var (Volt-Ampér-Reaktivní), kvar, Mvar. Zdánlivý výkon Voltampér, VA, kVA, MVA. Je zřejmé, že z hlediska jednotek jsou tyto jednotky totožné, pomáhají jen určit, který typ výkonu máme na mysli, uvádíme-li například na elektrickém motoru výkon 1kVA.
Pojem elektrické energie (práce) odvozujeme z pojmu výkonu. Pro elektrickou energii budeme užívat symbol a (okamžitá hodnota) a A (celková hodnota za určitý čas). Vztah mezi elektrickým výkonem a prací je (pro okamžité hodnoty) p=da/dt, pro celkovou energii (práci)
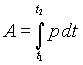
Jednotkou elektrické energie je joule (J), pro měření spotřeby elektřiny se ještě používá kilowatthodina (kWh). Nepleťte si kWh s ampérhodinou (Ah), to je jednotka "kapacity" akumulátoru, tj. jednotka náboje, který je možné do akumulátoru "uschovat" a opět odebrat.
Z dalších jednotek si jen připomeneme jednotku kapacity, farad (F) a indukčnosti, henry (H). Převodní vztahy k základním jednotkám můžeme odvodit několika způsoby, já dávám přednost použití Coulombova a Biot-Savartova zákona. Konstanta k v Coulombově zákoně F=k⋅q⋅q'/r2 závisí na prostředí, ve kterém jsou náboje q a q' umístěny. Je-li tímto prostředím vakuum, je tato konstanta (označíme ji ko) konstantou univerzální závislou pouze na volbě systému jednotek měření. V SI soustavě jednotek definitoricky stanovena jako ko=1/(4πεo), kde εo je tzv. permitivita vakua definovaná jako εo=107/(4πc2) Fm-1, kde c je rychlost světla ve vakuu. Číselně (s dostatečnou přesností) εo=8,854⋅10-12 F/m=8,854 pF/m. Obdobně v Biotově-Savartově zákoně ve tvaru B=k1⋅I/r je definována konstanta k1 pro vakuum jako k1=μo/2π, kde μo je permeabilita vakua, která má v soustavě SI hodnotu μo=4π⋅10-7 H/m=0,4π μH/m. Mezi konstantami εo a μo platí tedy definiční vztah εo a μoc2=1. Z těchto vztahů plynou následující převodní vztahy mezi H, F a základními jednotkami: H=kg·m2·s-2·A-2, F=A2·s4·kg-1·m-2. Farad i Henry jsou opět pro praktické účely mnohdy příliš velké jednotky; jejich zlomky se označují předponami obdobně jako je uvedeno pro proud.