Zápočtový test 2
Doba k řešení: 08. 01. 2021 09:00 — 09. 01. 2021 09:00
Čas načtení stránky: 14. 07. 2024 04:29
V testu jsou vždy 3 úlohy za 3 + 5 + 7 = 15 bodů.
Rozbalit všechna řešení Vytisknout
Úloha 1 (3 body, u3-1)
V experimentu chceme měřit rychlost protonů pocházejících z beta rozpadu neutronu n \(\rightarrow\) p e\(^-\) ν, které dosahují rychlostí do 400 km/s, metodou měření doby letu. Použijeme dva scintilační detektory vzdálené od sebe (2.000 ± 0.001) m a měříme časy průletu prvním a druhým scintilátorem. Určete metodou přenosu chyb standardní odchylku měřené rychlosti protonu v případě, že má uvedenou maximální rychlost a pokud použijeme scintilátory s rozlišením 1 ns. Chceme-li měření ještě zpřesnit, má smysl investovat do výrazně dražších scintilátorů s rozlišením 0.5 ns?Úloha 2 (3 body, u3-2)
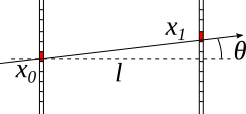
Experiment zkoumající pružný rozptyl mionů s velkou energií na protonech potřebuje přesně měřit polární úhel rozptylu \(\theta\). Dráha mionu je měřena ve dvou bodech vzdálených od sebe 3 m. Jakou standardní odchylku bude mít \(\theta = 5~\mathrm{mrad}\), pokud použijeme křemíkové detektory s velikostí pixelu \(80\times80~\mu\mathrm{m}^2\)?
Nápověda: Vzorec pro přenos chyby se zjednoduší, pokud uvážíme, že úhel je velmi malý. Pokud obdržíme signál v jednom pixelu o šířce \(\delta\), víme, že mion proletěl někde mezi hranicemi pixelu \((x_0, x_0 + \delta)\) s rovnoměrnou pravděpodobností.
Jako standardní odchylku ve změření poloh \(x_{0,1}\) budeme brát standardní odchylku rovnoměrného rozdělení na intervalu délky \(80~\mu\mathrm{m}\), tedy \(\sigma_x = \frac{80}{\sqrt{12}}~\mu\mathrm{m}\). Formulováno trochu jinak můžeme říct, že maximální chyba, které se dopouštíme když místo přesné pozice průletu dráhy pixelem použijeme jeho střed, je polovina šířky pixelu. Pro maximální chybu platí \(\sigma_x = \frac{40}{\sqrt{3}}~\mu\mathrm{m}\), což je to samé. Zanedbali jsme, že pixely jsou čtvercové a rozlišení v různých směrech se tedy liší.
Pro polární úhel platí \(\mathrm{tan}\,\theta = \frac{x_1-x_0}{l}\), takže \(\theta = \mathrm{tan}^{-1}\frac{x_1-x_0}{l}\). Spočteme si derivace pro přenos chyb, $$ \frac{\partial \theta}{\partial x_1} = - \frac{\partial \theta}{\partial x_0} = \frac{1}{\frac{(x_1-x_0)^2}{l^2} + 1} \frac{1}{l} \approx \frac{1}{l}, \qquad \frac{\partial \theta}{\partial l} \approx -\frac{x_1 - x_0}{l^2}. $$ Zde jsme využili toho, že pro malý úhel 5 mrad je jistě \(\frac{(x_1-x_0)^2}{l^2} = \mathrm{tan}^2\,\theta \ll 1\). Dosadíme, $$ \sigma_\theta^2 = 2\frac{\sigma_x^2}{l^2} + \frac{\sigma_l^2(x_1-x_0)^2}{l^4} = 2\frac{\sigma_x^2}{l^2} + \frac{\sigma_l^2\mathrm{tan}^2\,\theta}{l^2}. $$ $$ \sigma_\theta = \frac{1}{l} \sqrt{2\sigma_x^2 + \sigma_l^2\theta^2} = \frac{1}{3} \sqrt{\frac{2\cdot80^2\cdot10^{-12}}{12} + 2.5 \cdot 10^{-5} \sigma_l^2} = \frac{1}{3} \sqrt{1.1 \cdot 10^{-9} + 2.5 \cdot 10^{-5} \sigma_l^2}. $$ Do zadání jsem zapomněl napsat, jaká je \(\sigma_l\), nicméně vidíme, že pokud bude na úrovni 1 mm, což je jistě dosažitelné, bude už její vliv zanedbatelný a dostaneme $$ \sigma_\theta \approx \frac{1}{3} \sqrt{1.1 \cdot 10^{-9}} = 1 \cdot 10^{-5}. $$
Úloha 3 (5 bodů, u5-1)
Částice miony byly objeveny ve 30. letech v kosmickém záření. Rozpadají se na elektron a dvě neutrina. Jejich doba života se dá změřit tak, že vybereme mion, který se zastavil v železném absorbátoru, a čekáme na signál od rozpadového elektronu. Řekněme, že experiment naměřil následující hodnoty zpoždění mezi přicházejícím mionem a rozpadovým elektronem: $$ t_i = 7.69, 2.42, 3.61, 0.13, 1.20, 0.24~\mu\mathrm{s}. $$
Odvoďte vztah pro určení střední doby života metodou maximální věrohodnosti. Ověřte, jestli se jedná o nezaujatý estimátor. Spočítejte střední dobu života a její standardní odchylku (použijte metodu přenosu chyb, přesnost měření \(t_i\) považujte za dostatečnou, aby rozptyl \(t_i\) byl dán jen tím, že je to exponenciálně rozdělená náhodná proměnná).
Úloha 4 (5 bodů, u5-2)
Detektor kosmického záření zachytil následující počty signálů za den: $$ k_i = 109, 85, 107, 104, 104, 88. $$ Předpokládejte, že počet signálů za den má Poissonovo rozdělení. Odvoďte metodou maximální věrohodnosti estimátor parametru rozdělení \(\nu\). Ověřte, že se jedná o nezaujatý estimátor. Přenosem chyb určete jeho standardní odchylku.Poissonovo rozdělení udává pravděpodobnost \(k\) signálů za den jako $$ P(k|\nu) = \frac{\nu^k}{k!} e^{-\nu}. $$ Věrohodnostní funkce pro \(N\) pozorovaných počtů \(k_i\) je $$ \ln L = \sum_{i=1}^N P(k_i|\nu) = \sum_{i=1}^N \bigl(\ln\nu^{k_i} - \ln(k_i!) - \nu\bigr) = - N\nu + \ln\nu \sum_{i=1}^N k_i-\sum_{i=1}^N\ln(k_i!). $$ Nejpravděpodobnější \(\nu\) maximalizuje věrohodnost, $$ 0 = \frac{\partial \ln L}{\partial \nu} = -N + \frac{1}{\hat{\nu}} \sum_{i=1}^N k_i. $$ $$ \hat{\nu} = \frac{1}{N} \sum_{i=1}^N k_i. $$ Zaujatost estimátoru je \(b = E[\hat{\nu} - \nu] = E[\hat{\nu}] - \nu\). $$ E[\hat{\nu}] = \frac{1}{N} \sum_{i=1}^N E[k_i] = \frac{1}{N} \sum_{i=1}^N \nu = \nu. $$ Je tedy nezaujatý. Využili jsme toho, že očekávaná hodnota poissonovsky rozděleného \(k_i\) je \(\nu\).
Varianci určíme přenosem chyb, $$ \sigma_{\hat{\nu}}^2 = \sum_{i=1}^N \biggl( \frac{\partial\hat{\nu}}{\partial k_i}\biggr)^2\sigma_i^2 = \sum_{i=1}^N \frac{1}{N^2} \hat{\nu} = \frac{\hat{\nu}}{N} $$ Opět jsme použili, že \(k_i\) má Poissonovo rozdělení a jeho variance je tedy \(\sigma_i^2 = \nu\). Jako její odhad nám nezbývá než použít \(\hat{\nu}\).
Dosadíme čísla, $$ \hat{\nu} = \frac{1}{N} \sum_{i=1}^N k_i = 100.94, \qquad \sigma_{\hat{\nu}} = \sqrt{\frac{\hat{\nu}}{N}} = 4. $$ Výsledek zapíšeme jako \(\hat{\nu} = (101 \pm 4)\). Pro srovnání, skutečná hodnota použitá pro generování těch šesti čísel ze zadání, byla 100.
Úloha 5 (5 bodů, u5-3)
Byla provedena Monte Carlo simulace částicového experimentu, aby se zjstila efektivita detekce nějakého procesu. Vždy bylo vygenerováno 1000 událostí, by simulován průchod vzniklých částic experimentem a jejich odezva v detektorech. Nakonec byly signály z detektorů zrekonstruovány a sledovalo se, v kolika případech byla rekonstrukce správná (shodná s tím, co bylo generováno).
V jedné konfiguraci detektorů bylo dosaženo ve třech pokusech 851, 840 a 844 správných výsedků z 1000. V jiné konfiguraci to bylo 860, 848 a 847 úspěchů z 1000.
Odvoďte metodou maximální věrohodnosti estimátor pro pravděpodobnost úspěšné rekonstrukce jedné události. Ověřte, zda je to nezaujatý estimátor. Metodou přenosu chyb určete jeho odchylku a rozhodněte, zda je jedna z konfigurací signifikantně lepší než druhá.
Rekonstrukce jedné události je úspěšná s pravděpodobností, kterou označíme \(\epsilon\), nebo neúspěšná s pravděpodobností \(1-\epsilon\). Počítali jsme, kolik událostí z 1000 bylo správně zrekonstruováno. Tento počet \(k\), který jsme zjistili třikrát pro jednu konfiguraci a třikrát pro druhou, má tedy binomické rozdělení (výběr \(k\) úspěchů z \(N=1000\) pokusů), $$ P(k|N,\epsilon) = \frac{N!}{k!(N-k)!} \epsilon^k (1-\epsilon)^{N-k}. $$ Věrohodnostní funkce je $$ \ln L = \sum_{i=1}^M \ln P(k_i|N,\epsilon) = M \ln \frac{N!}{k_i!(N-k_i)!} + \sum_{i=1}^M k_i \ln \epsilon + \sum_{i=1}^M (N-k_i) \ln (1-\epsilon), $$ kde \(i\) čísluje pokusy, pro nás tedy \(M=3\). Hledáme takovou pravděpodobnost \(\epsilon\), že věrohodnost bude maximální, $$ 0 = \frac{\partial \ln L}{\partial \epsilon} = \sum_{i=1}^M \frac{k_i}{\hat{\epsilon}} - \sum_{i=1}^M \frac{N-k_i}{1-\hat{\epsilon}} = \frac{1}{\hat{\epsilon}} \sum_{i=1}^M k_i - \frac{1}{1-\hat{\epsilon}} \biggl(MN - \sum_{i=1}^M k_i\biggr). $$ Rovnici vynásobíme \(\hat{\epsilon}(1-\hat{\epsilon})\), $$ 0 = (1-\hat{\epsilon})\sum_{i=1}^M k_i - \hat{\epsilon} MN + \hat{\epsilon} \sum_{i=1}^M k_i $$ $$ \hat{\epsilon} = \frac{1}{MN} \sum_{i=1}^M k_i. $$ Zaujatost estimátoru je \(b = E[\hat{\epsilon} - \epsilon] = E[\hat{\epsilon}] - \epsilon\). $$ E[\hat{\epsilon}] = \frac{1}{MN} \sum_{i=1}^M E[k_i] = \frac{1}{MN} \sum_{i=1}^M N\epsilon = \epsilon. $$ Využili jsme toho, že očekávaná hodnota binomicky rozděleného \(k_i\) je \(N\epsilon\). Estimátor tedy není zaujatý.
Standardní odchylku zjistíme přenosem chyb, $$ \sigma_\hat{\epsilon}^2 = \sum_{i=1}^M \biggl( \frac{\partial\hat{\epsilon}}{\partial k_i}\biggr)^2 \sigma_i^2 = \sum_{i=1}^M\biggl(\frac{1}{MN}\biggr)^2 N\epsilon(1-\epsilon) = \frac{\hat{\epsilon}(1-\hat{\epsilon})}{MN}. $$ Stanardní odchylka jednoho měření (jednoho \(k_i\)), které má binomické rozdělení, je \(N\epsilon(1-\epsilon)\). Skutečné \(\epsilon\) jsme odhadli jako \(\hat{\epsilon}\).
Teď už jen dosadíme a dostaneme $$ \epsilon_1 = 0.845 \pm 0.007 \qquad \epsilon_2 = 0.852 \pm 0.006. $$ Mezi konfiguracemi není signifikantní rozdíl $$ \epsilon_1-\epsilon_2 = 0.007, \qquad \sigma_{\epsilon_1-\epsilon_2} = \sqrt{0.007^2 + 0.006^2} = 0.009. $$ Pro srovnání, pravděpodobnost, že normálně rozdělené číslo bude více než \(\frac{7}{9}\sigma\) od střední hodnoty (zde od nuly) je \(P(|x-\mu|>\frac{7}{9}\sigma) = 2F(-\frac{7\sigma}{9}) = 1 - \mathrm{erf}\frac{7}{9\sqrt{2}} = 44~\%.\)
Úloha 6 (7 bodů, u7-1)
Následující data proložte pomocí metody nejmenších čtverců závislostí \(\lambda(x) = a x\). Spočítejte \(\chi^2\) a jeho hladinu signifikance. Vyzkoušejte také fit konstantou \(\lambda(x) = c\) a také hypotézu \(\lambda(x) = 0\). Pro obě tyto hypotézy také spočítejte \(\chi^2\) a porovnejte hladiny signifikance všech třech hypotéz.
x y sigma 1.00 0.15 0.20 3.00 0.46 0.35 5.00 0.47 0.45 7.00 0.85 0.53 9.00 2.13 0.60
Metoda nejmenších čtverců spočívá v minimalizaci funkce $$ \chi^2 = \sum_{i=1}^N \frac{(y_i - \lambda(x_i))^2}{\sigma_i^2} $$ vůči parametrům funkce \(\lambda\). Pro funkce \(\lambda(x) = ax\) a \(\lambda(x) = c\) jsme řešení nalezli na 10. přednášce a výsledek jste mohli rovnou použít. Pro úplnost přidávám i to odvození. V prvním případě ve zkratce: $$ 0 = \frac{\partial \chi^2}{\partial a} = - 2 \sum_{i=1}^N \frac{y_i - \hat{a}x_i}{\sigma_i^2} x_i = - 2 \sum_{i=1}^N \frac{y_ix_i}{\sigma_i^2} + 2\hat{a} \sum_{i=1}^N \frac{x_i^2}{\sigma_i^2} = - 2 \langle xy \rangle + 2 \hat{a} \langle x^2 \rangle $$ $$ \hat{a} = \frac{\langle xy \rangle}{\langle x^2 \rangle}, \qquad\qquad \sigma_\hat{a}^2 = \sum_{i=1}^N \biggl( \frac{\partial \hat{a}}{\partial y_i}\biggr)^2 \sigma_i^2 = \sum_{i=1}^N \biggl( \frac{x_i}{\sigma_i^2 \langle x^2 \rangle} \biggr)^2 \sigma_i^2 = \frac{1}{\langle x^2 \rangle}. $$ Varianci jsme určili přenosem chyb. Pro konstantní funkci \(\lambda(x) = c\) minimalizací \(\chi^2\) dosataneme $$ 0 = \frac{\partial \chi^2}{\partial c} = - 2 \sum_{i=1}^N \frac{y_i - \hat{c}}{\sigma_i^2} = - 2 \sum_{i=1}^N \frac{y_i}{\sigma_i^2} + 2\hat{c} \sum_{i=1}^N \frac{1}{\sigma_i^2} = -2 \langle y \rangle + 2 \hat{c} \langle 1 \rangle. $$ $$ \hat{c} = \frac{\langle y \rangle}{\langle 1 \rangle}, \qquad\qquad \sigma_\hat{c}^2 = \sum_{i=1}^N \biggl( \frac{\partial \hat{c}}{\partial y_i}\biggr)^2 \sigma_i^2 = \sum_{i=1}^N \biggl( \frac{1}{\sigma_i^2\langle 1\rangle}\biggr)^2\sigma_i^2 = \frac{1}{\langle 1\rangle}. $$
Když do vzorců dosadíme čísla, obdržíme $$ \hat{a} = 0.16 \pm 0.04, \qquad \hat{c} = 0.4 \pm 0.1. $$ Spočítáme \(\chi^2\) pro \(\lambda(x) = \hat{a}x\), pro \(\lambda(x) = \hat{c}\) a pro \(\lambda(x) = 0\), $$ \chi^2_{\hat{a}x} = 2.2, \qquad \chi^2_{\hat{c}} = 10.6, \qquad \chi^2_0 = 18.6. $$ Hladina signifikance odpovídající např. \(\chi^2_{\hat{a}x}\) je pravděpodobnost, že pro novou náhodnou sadu měření vyjde \(\chi^2 > \chi^2_{\hat{a}x}\) za předpokladu, že platí \(y_i = \hat{a}x_i \pm \sigma_i\). Můžeme ji určit díky tomu, že \(\chi^2\) této nové náhodné sady bodů je náhodná proměnná s takzvaným \(\chi^2\)-rozdělením. To je popsané distribuční funkcí \(F(\chi^2\|n_\mathrm{df})\) s jedním parametrem \(n_\mathrm{df} = N - M\), zvaným počet stupňů volnosti. \(N\) je počet bodů a \(Ḿ=1\) je počet fitovaných parametrů. Distribuční funkce je standardně dostupná v programech na zpracování dat, případně můžeme použít také tabulku. $$ P_{\hat{a}x} = 1 - F(2.2|4) = 0.71, \qquad P_{\hat{c}} = 1 - F(10.6|4) = 0.03, \qquad P_0 = 1 - F(18.6|5) = 0.002. \qquad $$ Pokud si stanovíme přísný limit pravděpodobnosti 1 %, můžeme vyloučit pouze hypotézu \(\lambda(x) = 0\). Pokud nám stačí vyšší limit, např. 5 %, můžeme vyloučit i hypotézu, že \(\lambda(x)\) je konstantní (jenom 3 % všech možných sad pěti čísel \(y_i = c \pm \sigma_i\) mají \(\chi^2\) takto vysoký nebo ještě vyšší).
Úloha 7 (7 bodů, u7-2)
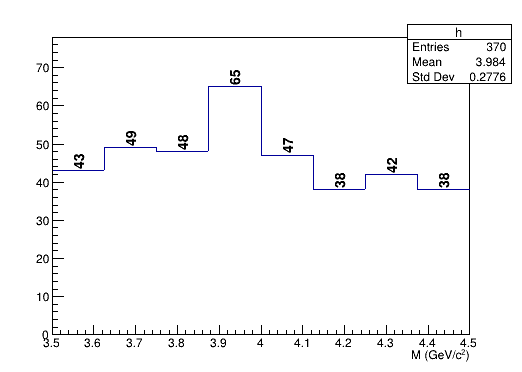
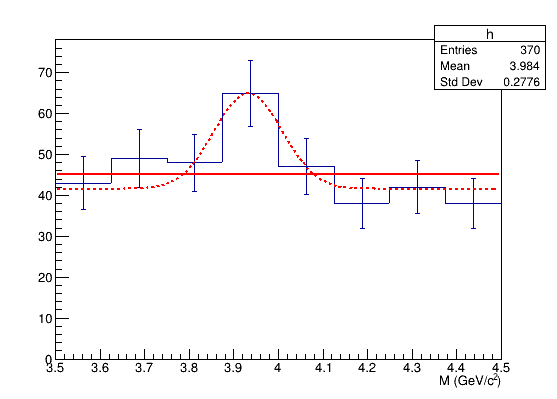
Hypotetický experiment studoval produkci několika částic a objevil peak v jejich invariantní hmotě. Mohlo by to znamenat, že jejich produkce probíhá v té oblasti přes vázaný stav – přes dosud neznámou částici. Nebo se jedná jen o náhodný šum.
Vyjděte z nulové hypotézy, že se tento histogram dá popsat rovnoměrným rozdělením (počet událostí ve všech binech \(n_i = c, \forall i\)). Určete takovou hodnotu konstanty \(c\), která minimalizuje sumu čtverců odchylek. Spočítejte \(\chi^2\) a určete hladinu signifikance.
Spočítejte \(\chi^2\) a hladinu signifikance také pro hypotézu konstantního pozadí a gaussovského peaku $$ n_i = 41 + 23 \exp\biggl( -\frac{(M_i - 3.9)^2}{2\cdot0.08^2}\biggr) $$ Nezapomeňte, že počet událostí v binu je náhodná proměnná, která má přibližně Poissonovo rozdělení.
Hledáme \(c\), které minimalizuje $$ \chi^2 = \sum_{i=1}^m \frac{(n_i - c)^2}{\sigma_i^2} = \sum_{i=1}^m \frac{(n_i - c)^2}{n_i}, $$ kde \(m\) je počet binů, \(n_i\) je počet událostí v i-tém binu a \(\sigma_i^2\) je jeho rozptyl. \(n_i\) má přibližně Poissonovo rozdělení, pro které \(\sigma_i^2 = V[n_i] = E[n_i]\). To sice přesně neznáme, ale můžeme ho odhadnout jako \(n_i\). Jiná možnost s mírně jiným výsledkem by byla odhadnout ho jako \(c\).
Pro minimum platí $$ 0 = \frac{\partial \chi^2}{\partial c} = -2 \sum_{i=1}^m \frac{n_i - c}{n_i} = -2 m + 2 c \sum_{i=1}^m \frac{1}{n_i}. $$ $$ c = m \biggl( \sum_{i=1}^m \frac{1}{n_i} \biggr)^{-1} = 45. $$ Můžeme odvodit i standardní odchylku, $$ \frac{\partial c}{\partial n_j} = m \biggl( \sum_{i=1}^m \frac{1}{n_i} \biggr)^{-2} \frac{1}{n_j^2} = \frac{c^2}{m n_j^2}. $$ $$ \sigma_c = \sqrt{\sum_{i=1}^m \biggl( \frac{\partial c}{\partial n_i} \biggr)^2 \sigma_i^2} = \frac{c^2}{m} \sqrt{\sum_{i=1}^m \frac{1}{n_i^3}} = 2. $$ Mohli jsme také rovnou využít výsledku ze cvičení 10, kde jsme pro problém fitu konstantou nalezli řešení jako vážený průměr. Výrazy jsou ekvivalentní.
\(\chi^2\) je pro \(c=45\) (tedy ve svém minimu) roven \(\chi^2_0 = 9.6\). Počet stupňů volnosti je počet binů mínus počet parametrů, tedy \(m-1=7\). Hladina signifikace je $$ P(\chi^2 > \chi^2_0|n_\mathrm{df}=7) = 1 - F_{\chi^2}(\chi^2_0|n_\mathrm{df}=7) = 21~\%. $$ Rozhodně tedy nelze vyloučit, že tento histogram obsahuje pouze rovnoměrně rozdělené hmoty.
Pro model s peakem budeme potřebovat středy binů. Histogram je od \(3.5~\mathrm{GeV}/c^2\) do \(4.5~\mathrm{GeV}/c^2\) a má 8 binů. Šířka binu je tedy \(\frac{1}{8}~\mathrm{GeV}/c^2\). Střed prvního binu je \(3.5 + \frac{1}{16}~\mathrm{GeV}/c^2\). Střed \(i\)-tého binu je \(M_i = 3.5 + i\frac{1}{8} - \frac{1}{16}~\mathrm{GeV}/c^2\).
Příspěvek peaku k \(\chi^2\) je významný ve 4. binu, kde leží maximum. Trochu přispěje ještě v sousedních binech, jinak už je zanedbatelný. Pro posouzení kvality fitu potřebujeme vedět, že model má 4 volné parametry (konstanta a střed, výška a šířka peaku). Číselně vychází $$ \chi^2_1 = 1.8, \qquad P(\chi^2 > \chi^2_1|n_\mathrm{df}=4) = 1 - F_{\chi^2}(\chi^2_1|n_\mathrm{df}=4) = 77~\%. $$ Popisuje tedy data lépe, ale na konstatování objevu to nestačí. Bylo by potřeba nejdříve vyvrátit nulovou hypotézu a to se nepodařilo.
Pro lepší představu si můžeme vykreslit histogram s chybovými
úsečkam a s oběma modelovými funkcemi. Konstantní model vypadá
i na pohled celkem kompatibilně s daty.