Terminální rychlost

výpočet terminální rychlosti při pádu člověka z letadla numerickým řešením pohybové rovnice

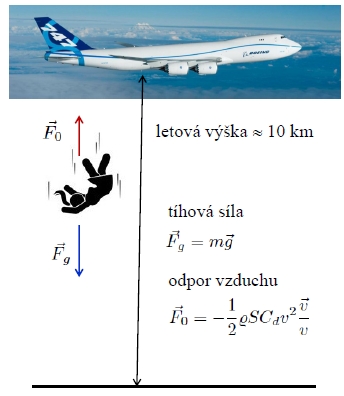
importujeme knihovny numpy (na numerické výpočty) a matplotlib (na kreslení grafů)

import numpy as np
import matplotlib.pyplot as plt

konstanty

g = 9.82 #gravitační zrychlení m/s^2
Cd = 0.5 #součinitel odporu pro kouli
rho = 1.29 #hustota vzduch (kg/m^3)
mu = 2e-5 #viskozita vzduchu (Pa s)
d_c = 0.8 #'velikost' člověka (0.8 mm)
d_p = 0.01 #'velikost' pavouka (1 cm)
S_c = np.pi*(d_c/2)**2 #průřez člověka
S_p = np.pi*(d_p/2)**2 #průřez pavouka
m_c = 80 #hmostnost člověka (80 kg)
m_p = 0.5e-3 #hmostnost pavouka (0.5 g)
h0 = 10e3 #letová výška letadla (10 km)

Odporová síla prostředí:

• pokud je Reynoldsovo číslo $Re < 10^3$:

$F_o = \frac{1}{2}\rho S C_d v$ (Stokesův zákon)

• pokud je Reynoldsovo číslo $Re > 10^3$:

$F_o = \frac{1}{2}\rho S C_d v^2$ (Newtonův zákon)

def Fo(v,rho,Cd,S):
    L = np.sqrt(S) #charakteristický rozměr předmětu
    Re = v*rho*L/mu #Reynoldsovo číslo
    vc = 1e3*mu/(rho*L)
    if Re<1e3:
        return 0.5*Cd*rho*S*vc*v #Stokesův režim
    else:
        return 0.5*rho*Cd*S*v**2 #Newtonův režim

Zvolíme max. čas $t_{max}$, po který budeme pohyb sledovat, a časový krok $dt$ pro numerické řešení.

tmax = 1000 #doba, po kterou šikmý vrh sledujeme (zde 1000 s)
dt = 0.1 #časový krok pro numerický výpočet derivace (zde desetina sekundy)

Vytvoříme pole t obsahující časy,
pole x a y obsahující souřadnice v těchto časech
pole vx a vy obsahující rychlosti v těchto časech

t = np.arange(0,tmax,dt) #pole časů
y = np.empty(np.size(t)) #pole y-ových souřadnic
vy = np.empty(np.size(t)) #pole y-ových složek rychlostí

počáteční podmínky:

• hmotný bod je v čase $t = 0$ ve výšce $h_0$
• v čase $t = 0$ má nulovou rychlost.

y[0] = h0 # y-ová souřadnice v čase t = 0
v0 = 0 #velikost rychlosti v čase t = 0 
vy[0] = v0-g*dt/2 - Fo(v0,rho,Cd,S_c)/m_c*dt/2 # y-ová složka rychlosti  v čase t = 0 + dt/2

Nyní numericky vyřešíme pohybovu rovnici pro pád z letadla $$m\ddot{y} = -mg - F_o.$$

i = 0 #index pro cyklus přes jednotlivé časy
imax = np.size(t) #max. hodnota indexu (abychom nepřekročily rozsah pole)
istop = 0 #přepínač kontrolující jestli předmět dopadl na zem, pokud dopadne na zem -> istop=1 a cyklus skončí
while istop == 0 and i < np.size(t)-1: #cyklus běží dokud předmět nespadne na zem nebo neprojdu celé pole časů
    i+=1
    y[i] = y[i-1]+vy[i-1]*dt #update y-ové souřadnice pro čas t -> d + dt
    if y[i]<0: #spadlo to na zem
        istop = 1
        imax_c = i
    vy[i] = vy[i-1]-g*dt-Fo(np.abs(vy[i-1]),rho,Cd,S_c)/m_c*vy[i-1]/np.abs(vy[i-1])*dt #update y-ové složky rychlosti pro čas t -> d + dt    
    

Bez odporu vzduchu bude $v_y = -gt$.

Porovnáme časovou závislost rychlosti s a bez odporu vzduchu

plt.plot(t[0:imax_c],g*t[0:imax_c],c='blue',ls='dashed',label="bez odporu vzduchu")
plt.plot(t[0:imax_c],np.abs(vy[0:imax_c]),c='red', label="s odporem vzduchu")
plt.xlabel("čas (s)")
plt.ylabel("velikost rychlosti (m/s)")
plt.xlim(0,)
plt.ylim(0,5*np.abs(vy[imax_c]))
plt.legend()
plt.show()

print(f"člověk: terminální rychlost: {np.abs(vy[imax_c]):5.1f} m/s (se započítaným odporem vzduchu)")

člověk: terminální rychlost:  69.6 m/s (se započítaným odporem vzduchu)

Zopakujme výpočet pro malého pavouka, který vypadl ze stejného letadla.

• hmotnost pavouka je 0.5 g
• velikost pavouka je 1 cm

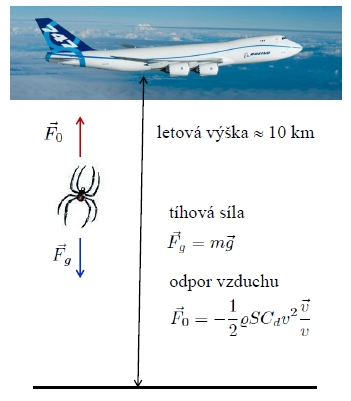
d_p = 0.01 #'velikost' pavouka (1 cm)
S_p = np.pi*(d_p/2)**2 #průřez pavouka
m_p = 0.5e-3 #hmostnost pavouka (0.5 g)

y_p = np.empty(np.size(t)) #pole y-ových souřadnic pro pavouka
vy_p = np.empty(np.size(t)) #pole y-ových složek rychlostí pro pavouka

y_p[0] = h0 # y-ová souřadnice v čase t = 0 pro pavouka
v0_p = 0 #velikost rychlosti v čase t = 0 pro pavouka
vy_p[0] = v0_p-g*dt/2 - Fo(v0,rho,Cd,S_p)/m_p*dt/2 # y-ová složka rychlosti  v čase t = 0 + dt/2 pro pavouka

i = 0 #index pro cyklus přes jednotlivé časy
imax = np.size(t) #max. hodnota indexu (abychom nepřekročily rozsah pole)
istop = 0 #přepínač kontrolující jestli předmět dopadl na zem, pokud dopadne na zem -> istop=1 a cyklus skončí
while istop == 0 and i < np.size(t)-1: #cyklus běží dokud předmět nespadne na zem nebo neprojdu celé pole časů
    i+=1
    y_p[i] = y_p[i-1]+vy_p[i-1]*dt #update y-ové souřadnice pro čas t -> d + dt pro pavouka
    if y_p[i]<0: #spadlo to na zem
        istop = 1
        imax_p = i
    vy_p[i] = vy_p[i-1]-g*dt-Fo(np.abs(vy_p[i-1]),rho,Cd,S_p)/m_p*vy_p[i-1]/np.abs(vy_p[i-1])*dt #update y-ové složky rychlosti pro čas t -> d + dt pro pavouka   
    

Srovnání terminálních rychlostí pro člověka a pavouka

plt.plot(t[0:imax_c],np.abs(vy[0:imax_c]),c='red', label="člověk")
plt.plot(t[0:imax_p],np.abs(vy_p[0:imax_p]),c='green', label="pavouk")
plt.xlabel("čas (s)")
plt.ylabel("velikost rychlosti (m/s)")
plt.ylim(0,)
plt.xscale('log')
plt.legend()
plt.show()

print(f"člověk: terminální rychlost: {np.abs(vy[imax_c]):5.1f} m/s (se započítaným odporem vzduchu), doba pádu {t[imax_c]/60:4.2f} min")
print(f"pavouk: terminální rychlost: {np.abs(vy_p[imax_p]):5.1f} m/s (se započítaným odporem vzduchu), doba pádu {t[imax_p]/60:4.2f} min")

člověk: terminální rychlost:  69.6 m/s (se započítaným odporem vzduchu), doba pádu 2.48 min
pavouk: terminální rychlost:  13.9 m/s (se započítaným odporem vzduchu), doba pádu 11.99 min