Trajektorie pohybu hmotného bodu na pružině po

importujeme knihovny numpy (na numerické výpočty) a matplotlib (na kreslení grafů)

import numpy as np
import matplotlib.pyplot as plt

Zadáme parametry pro rovnoměrný pohyb po kružnici:
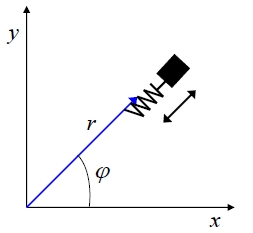
$r$ je poloměr kruhové trajektorie
$T$ je perioda pohybu (tj. doba za kterou hmotný bod oběhne celou kružnici)
úhlová frekvence pohybu bude tedy $\omega = \frac{2\pi}{T}$

r = 1 #poloměr trajektorie 1 m
T = 1 #perioda pohybu 1 s
omega = 2 *np.pi/T #=uhlová frekvence

Zvolíme frekvenci kmitů pružiny f_p a amplitudu kmitů pružiny A_p

f_p = 7/T #frekvence kmitů pružiny bude 7-krát vyšší než frekvence pohybu po kružnici
A_p = r #amplituda kmitů pružiny rovna poloměru kružnice

Vytvoříme pole t obsahující časy, v kterých chceme vypočítat souřadnice hmotného bodu

t = np.linspace(0,T,1000) #rozdělíme periodu na 1000 částí

Vypočítáme souřadnice hmotného bodu v jednotlivých časech
$$x = \left (r-A_{p}\text{sin}(2\pi f_{p}t)\right ) \text{cos}(\omega t)$$ $$y = \left (r-A_{p}\text{sin}(2\pi f_{p}t)\right ) \text{sin}(\omega t)$$ Tyto souřadnice budou v polích x a y

x=(r-A_p*np.sin(2*np.pi*f_p*t))*np.cos(omega*t) #x-ová souřadnice
y=(r-A_p*np.sin(2*np.pi*f_p*t))*np.sin(omega*t) #y-ová souřadnice

Nyní můžeme nakreslit graf trajektorie

fig,ax=plt.subplots(figsize=(6,6)) #změníme velikost obrázku aby to byl čtverec
ax.plot(x,y) #vytvoření grafu
ax.set_xlabel("x") #označení vodorovné osy
ax.set_ylabel("y") #označení svislé osy
plt.show() #vykreslení grafu

Můžeme vykreslit také časovou závislost souřadnic

plt.plot(t,x,c='blue', label="x-ová souřadnice") 
plt.plot(t,y,c='red', label="y-ová souřadnice") 
plt.xlabel("čas")
plt.ylabel("souřadnice")
plt.legend()
plt.show()