Koaxiální vedení (koaxiální vlnovod)

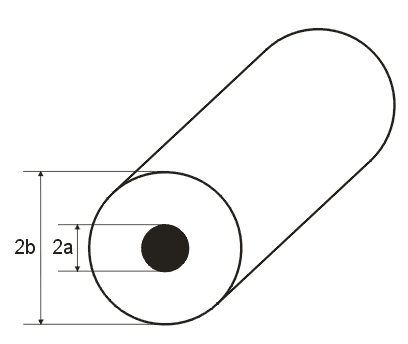
Obr.3.4.1 Řez koaxiálním vedením

Na obr. 3.4.1 je znázorněno koaxiální vedení, které se též někdy označuje jako koaxiální vlnovod. Zajímá nás pouze útvar s kruhovým průřezem. Na první pohled je patrné, že vzhledem k tomu, že tento vlnovod je obklopen dvěma vodivými válcovými plochami, může tímto útvarem téci i stejnosměrný proud.Vlnovod je propustný pro libovolně nízkou frekvenci a kritická frekvence je nulová, kritická vlnová délka  je nekonečná a platí, že .

Je-li však , není možné, aby se šířily vlny TE, TM a jedině možná vlna je TEM. Strukturu této vlny v koaxiálním vlnovodu kruhového průřezu určíme snadno.

Za prvé víme, že . Za druhé pro  neplatí rovnice (3.1.7) až (3.1.10). Víme, že vlna je TEM, tj. šíří se ve směru z a má složky E_r , H_f . Vzhledem k tomu, že není důvodu, aby struktura pole závisela na frekvenci je E_r (r,z) obdobné, jako struktura pole ve válcovém kondenzátoru, takže

    kde    

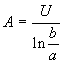
Obdobně pro magnetické pole H_f dostaneme

,

kde 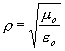 je vlnový odpor vakua.

K těmto výsledkům můžeme ovšem dojít též pomocí Maxwellových rovnic (ve válcových souřadnicích), položíme-li E_z = H_z =0, a dále

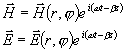
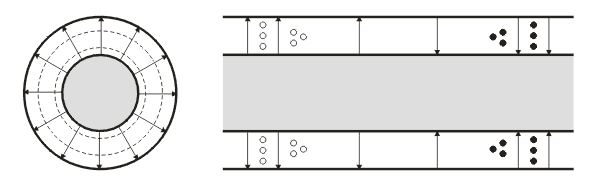
Obr.3.4.2 Struktura vlny TEM

Koaxiálním vlnovodem se však mohou též šířit vlny TE,TM. To,že dvojitý vodivý obal umožňuje existenci vln TEM (s kritickou frekvencí nulovou), nezajišťuje ještě, že není možné šíření vlny pro níž  . Pak ovšem bude pro složky E_z (resp. H_z) platit rovnice (3.3.1) a pro ostatní složky rovnice (3.3.5) až (3.3.7). Řešení rovnice (3.3.1) však nemůžeme vyjádřit ve tvaru (3.3.2) nebo (3.3.9), tj. pouze pomocí Besselových funkcí J_n , neboť bychom nemohli splnit okrajové podmínky na dvou plochách (r = a ; r = b), které nyní obklopují vlnovod. Musíme tedy napsat obecné řešení Besselovy rovnice, takže pro vlnu TE platí

      (3.4.1)

kde N_n  jest Neumanova funkce. Poněvadž E_f = 0 pro r = a i pro r = b a z Maxwellových rovnic plyne, že E_f~ dostaneme z (3.4.1)

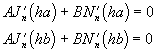
odtud

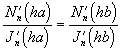      (3.4.2)

pro  n =0,1,2,3,......

Obdobně dostaneme pro vlnu TM z E_z = 0 pro r = a i pro r =  b obdobnou rovnici

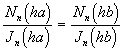      (3.4.3)

(3.4.2) a (3.4.3) jsou transcendentní rovnice pro určení  h a odtud příslušných kritických vlnových délek. Vzhledem k tomu, že řešený problém je takto málo „průhledný“, uchýlíme se k tomu, že budeme hledat přibližné řešení pro mezní případy: velmi malé a velmi velké hodnoty argumentů Besselových a Neumannových funkcí při nějaké hodnotě indexu n. 

Zvolíme n = 0 a předpokládáme, že . Potom

Dosazením do (3.4.3) dostaneme

Mezní případ (pro velmi nízké frekvence) je takový, že h = 0, ale to je opět vlna TEM.

Pro druhý mezní případ  (velmi vysoké frekvence), použijeme asymptotické formule pro Besselovy a Neumannovy funkce, tj. 

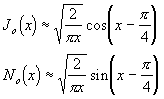
Dosazením do (3.4.3) dostaneme po úpravě

, odkud

 a kritická vlnová délka je

Kritická vlnová délka je velmi malá, kritická frekvence vysoká. Tak vysoké frekvence se však reálným koaxiálním vedením nemohou šířit pro velký útlum, což je vysvětleno dále. Docházíme k závěru, že jediný vid, který se reálně může šířit koaxiálním vedením je vlna TEM.

<<< předchozí | hlavní stránka | další >>>