Ideální vlnovod kruhového průřezu

Na obr. 3.3.1 je znázorněn vlnovod kruhového průřezu. Z geometrie plyne, že vektory pole je vhodné vyjádřit jako funkce válcových souřadnic

       ;        

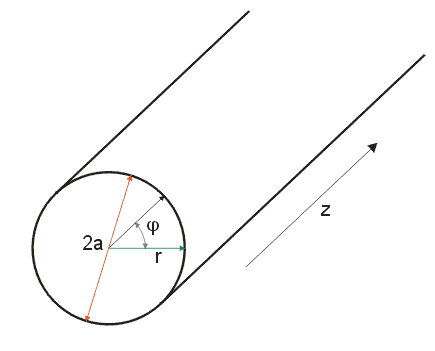
Obr.3.3.1 Řez vlnovodem kruhového průřezu

Vzhledem k tomu, že opět předpokládáme šíření vlny ve směru osy z , píšeme symbolicky pro ideální vlnovod

   ;   

Dále pak postupujeme stejně jako v případě vlnovodu obdélníkového průřezu pomocí Maxwellových rovnic. Operace div a rot však musíme vyjádřit ve válcových souřadnicích:

a analogicky pro vektor .

Opět rozdělíme vlny na TM(E) a TE(H). Pro vlnu TM dostaneme vlnovou rovnici pro osovou složku intenzity elektrického pole

                    (3.3.1)

Řešení hledáme ve tvaru   

a dostaneme po jednoduché úpravě  

Zvolíme , aby  a rovnice (3.3.1) přejde v

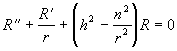
Snadno se přesvědčíme - substitucí  a vyjádřením ,že se jedná o Besselovu rovnici pro  s indexem n. Besselova rovnice s indexem n má obecně tvar .

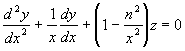Jejím řešením je Besselova funkce argumentu hr s indexem n, takže

                        (3.3.2)

Okrajová podmínka  vede k požadavku

                                        (3.3.3)

K určení h musíme tedy najít nulové body příslušné Besselovy funkce. (Jsou tabelovány). Označíme-li jako n_ni-itý kořen rovnice (3.3.3), můžeme h vyjádřit pomocí vztahu

Z podmínky  

můžeme opět určit kritickou vlnovou délku

                 (3.3.4)

Je vidět, že kritická vlnová délka (a též struktura vlny) závisí opět na dvou indexech; n je index Besselovy funkce a má hodnoty n =0,1,2,3,..., kdežto i čísluje nulové body této funkce a probíhá hodnoty i = 1,2,3,...

Při stejném označení jako u obdélníkového vlnovodu dostaneme pro vlnu TM₀₁

Z Maxwellových rovnic dostaneme dále obdobným způsobem jako u vlnovodu obdélníkového průřezu transverzální složky elektrického a magnetického pole odpovídající rovnicím (3.1.7) až (3.1.10)

Pro vlnu TE(H) ve vlnovodu kruhového průřezu dostaneme analogicky s rovnicí (3.3.2)

           (3.3.9)

s okrajovou podmínkou . Protože podle (3.3.6) platí   ~ , bude tato podmínka splněna, když . Označíme-li nulové body této rovnice jako  , kde n je opět index Besselovy funkce ( n =0,1,2,3,...) a i čísluje kořeny (i =1,2,3, …), máme a pro kritickou vlnovou délku vychází  .

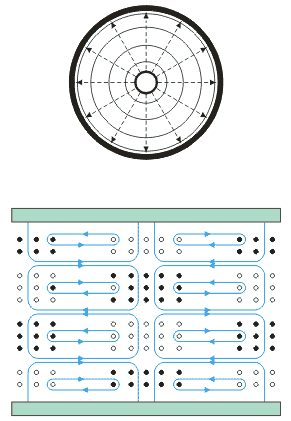
Vlna	TM01	TM02	TM11
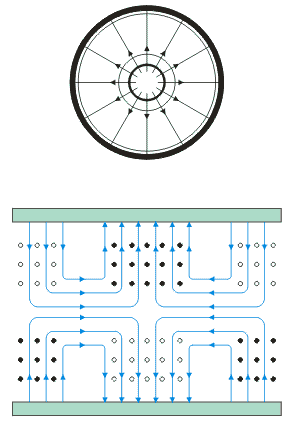
příčný řez                   podélný řez
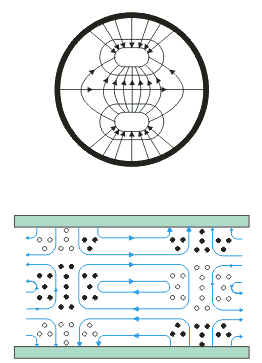složky	Ez, Er, Hf	Ez, Er, Hf	Ez, Er, Ef, Hr,Hf
l0	2,61a	1,14a	1,64a

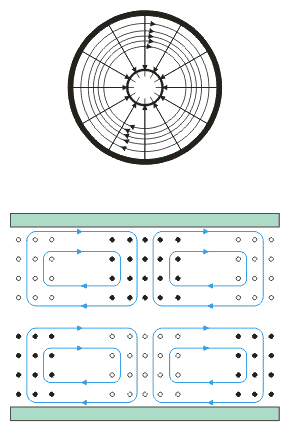
Vlna	TE01	TE11
příčný řez                   podélný řez
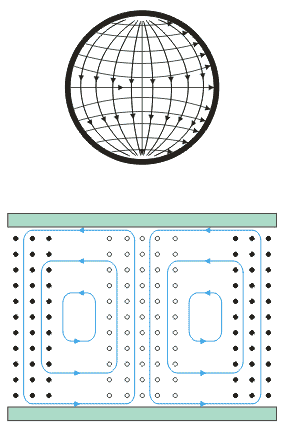složky	Hz, Hr, Ef	Hz, Hr, Hf, Er,Ef
l0	1,64a	3,41a

Obr.3.3.2 Vlna TM_01, TM₀₂, TM_11, TE_01, TE₁₁

Nebudeme zde opakovat  úvahy o konstrukci siločar, postup je stejný jako u vlnovodů obdélníkového průřezu. Na obr. 3.3.2 jest znázorněna struktura pole pro několik nejnižších vidů. Je zajímavé, že nejdelší kritickou vlnovou délku  má vlna TM₀₁ , jejíž struktura v rovině z = konst není nejsymetričtější (větší symetrii vykazují vlny  TM_01, TE₀₁).

<<< předchozí | hlavní stránka | další >>>