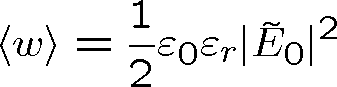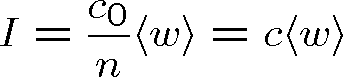1.6 Intenzita světla
V optice se často používá intenzita světla, která souvisí s hustotou výkonu přenášeného světelnou vlnou. Lze ji zavést pomocí Poyntingova vektoru. Poyntingův vektor je definován
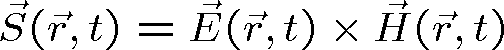 |
(1.67) |
Pro rovinné vlny (srov. rov. (1.35, 1.38)) je
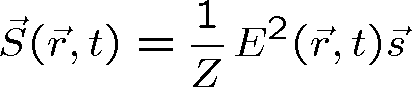 |
(1.68) |
míří tedy ve směru šíření vln. Například dosazením za velikost intenzity monochromatického elektrického pole (oscilujícího na frekvenci ω) ze vztahu (1.61) zjistíme, že velikost Poyntingova vektoru obsahuje časově neproměnnou část a část oscilující na frekvenci 2 ω. Intenzita světla se pro obecnou elektromagnetickou vlnu definuje jako časová střední hodnota velikosti Poyntingova vektoru, tedy jako časová střední hodnota hustoty výkonu dopadajícího na jednotkovou plochu kolmou na směr šíření vln
 (středování v čase odstraní oscilace na frekvenci 2 ω)
(středování v čase odstraní oscilace na frekvenci 2 ω)
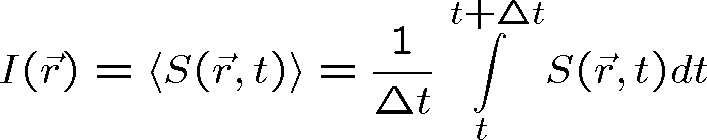 |
(1.69) |
Zde
 je doba středování. V případě rovinné vlny je podle rov. (1.68)
je doba středování. V případě rovinné vlny je podle rov. (1.68)
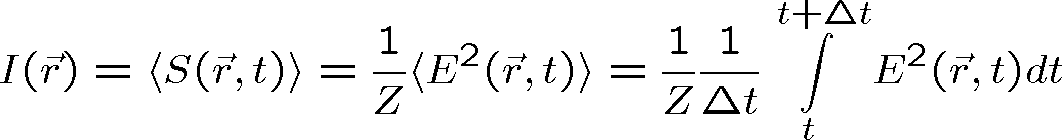 |
(1.70) |
Intenzitu světla pro harmonickou (tj. monochromatickou) rovinnou vlnu můžeme vyjádřit pomocí komplexní amplitudy elektrického pole, dosadíme-li do posledního vztahu vyjádření pole pomocí rov. (1.61). Rozvineme-li druhou mocninu a uvážíme-li, že časové střední hodnoty exponenciálních funkcí
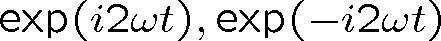 jsou nulové, máme
jsou nulové, máme
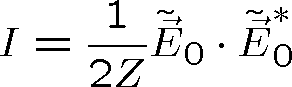 |
(1.71) |
Podle rov. (1.40) lze přepsat impedanci Z pomocí indexu lomu prostředí10
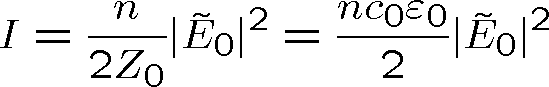 |
(1.72) |
Intenzitu světla můžeme vyjádřit pomocí střední časové hodnoty hustoty energie elektromagnetického pole spojeného s rovinnou světelnou vlnou w (
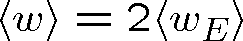 )
)
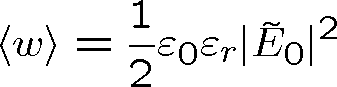 |
(1.73) |
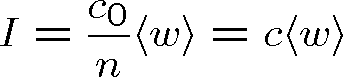 |
(1.74) |
Vyjádření intenzity světla jako střední časové hodnoty velikosti Poyntingova vektoru (1.69) je obecné, pro vlny se složitějšími prostorovými závislostmi může intenzita světla záviset na polohovém vektoru. Pokud se amplitudy vln mění v čase, může být i intenzita světla funkcí času (světelné záblesky, pulsy). Časové středování, jak jsme je popsali výše, je totiž třeba provádět tak, aby se vystředovaly časové změny související s oscilacemi polí na nosné frekvenci (ve viditelné oblasti doby řádově 10 -15 s). Při reálném sledování intenzity světla "se středuje" přes dobu danou časovou odezvou použitého detektoru (například fotodioda, oko).
Výrazy (1.72) a (1.74) pro intenzitu světla jsme získali pomocí vztahu mezi vektorem elektrického a magnetického pole příčné rovinné vlny. V kapitole 10 (odstavec 10.1.3) ukážeme, že platí i pro obecnější pole v aproximaci geometrické optiky. I ve většině dalších případů, s nimiž se v optice setkáváme, lze intenzitu světla vyjádřit s dobrou přesností pomocí rov. (1.72).
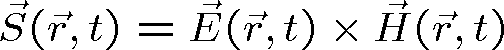
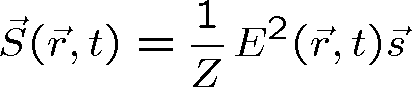
 (středování v čase odstraní oscilace na frekvenci 2 ω)
(středování v čase odstraní oscilace na frekvenci 2 ω)
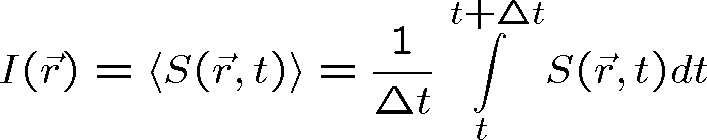
 je doba středování. V případě rovinné vlny je podle rov. (1.68)
je doba středování. V případě rovinné vlny je podle rov. (1.68)
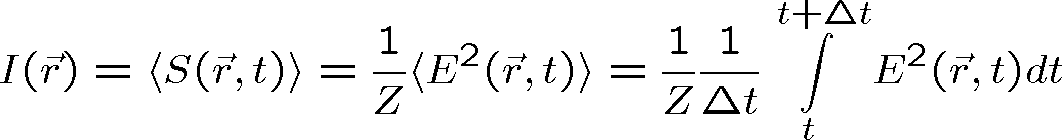
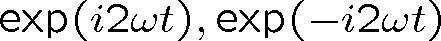 jsou nulové, máme
jsou nulové, máme
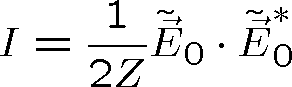
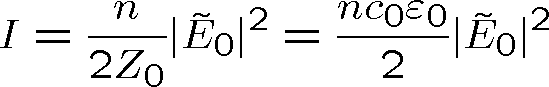
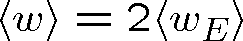 )
)