Rovnici (5.24) můžeme přepsat na tvar
 |
(5.25) |
Chová-li se plyn jako ideální, musí být pro látkové množství 1 mol (N = {NA}) součin tlaku p a molárního objemu Vm roven součinu molární plynové konstanty R a termodynamické teploty T(pVm = RT). Protože m0NA je molární hmotnost Mm plynu, můžeme termodynamickou teplotu plynu vyjádřit vztahem
 |
(5.26) |
Vztah (5.26) můžeme použít obráceně. Známe-li termodynamickou teplotu plynu, můžeme jednoznačně určit takzvanou střední kvadratickou rychlost vk
 |
(5.27) |
Největší střední kvadratickou rychlost při dané teplotě budou mít molekuly vodíku H2. Jejich molární hmotnost je Mm = 2 g . mol-1. Protože molární plynová konstanta R
 8,3 J . K-1 . mol-1, bude mít molekulový vodíkový plyn při teplotě 300 K střední kvadratickou rychlost asi 1,9 km . s-1.
8,3 J . K-1 . mol-1, bude mít molekulový vodíkový plyn při teplotě 300 K střední kvadratickou rychlost asi 1,9 km . s-1.
5.6 Teplota plynu a střední kvadratická rychlost molekul
než rychlost střely z pušky. Kdyby při průměrné teplotě vyšších vrstev atmosféry byla střední kvadratická rychlost molekul větší než I. kosmická rychlost, opouštěly by molekuly zemskou atmosféru.
V předchozím textu jsme uváděli důvody, proč střední hodnota druhé mocniny libovolné složky rychlosti je rovna právě jedné třetině střední hodnoty druhé mocniny rychlosti, např.
 . Střední hodnota druhé mocniny x-ové složky rychlosti je proto rovna
. Střední hodnota druhé mocniny x-ové složky rychlosti je proto rovna
 |
(5.28) |
kde k = R/NA je Boltzmannova konstanta k
 1,38 . 10-23 J . K-1. Veličinu v2 můžeme spočítat též podle vztahu (5.7c)
1,38 . 10-23 J . K-1. Veličinu v2 můžeme spočítat též podle vztahu (5.7c)
 |
(5.29) |
Hustotu pravděpodobnosti
 jsme vypočítali v článku 5.3. Porovnáním výsledku z (5.29) s hodnotou (5.28) určíme dosud přesně nespecifikované vyjádření rozptylu
jsme vypočítali v článku 5.3. Porovnáním výsledku z (5.29) s hodnotou (5.28) určíme dosud přesně nespecifikované vyjádření rozptylu
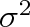 .
.
Po dosazení z (5.18) do (5.29) dostaneme výraz
 |
V článku 5.3 jsme vypočítali integrál
 |
; derivace
 |
. Použijeme-li tohoto výsledku, bude
pro

 |
(5.30) |
čili
 .
.
Střední hodnota druhé mocniny složky rychlosti je rovna rozptylu
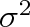 . Hustotu
. Hustotu
pravděpodobnosti můžeme s přihlédnutím ke vztahu (5.28) zapsat ve tvaru
 |
(5.31) |
S rostoucí teplotou se zvyšuje střední kvadratická rychlost a rozptyl a roste pravděpodobnost výskytu molekul s velkou absolutní hodnotou libovolné ze složek rychlosti. Střední hodnota složky rychlosti, která je zároveň i hodnotou
Vrátíme se ke stavové rovnici
 |
kde
 je střední kvadratická hodnota libovolné složky rychlosti
je střední kvadratická hodnota libovolné složky rychlosti
 |
kde jsme za
 použili Boltzmannovu konstantu (k = 1,38 10-23 J K-1).
použili Boltzmannovu konstantu (k = 1,38 10-23 J K-1).
Nyní můžeme přepsat vztah pro hustotu pravděpodobnosti složky rychlosti (5.18) do obvykle používaného tvar
 |
neboť jsme již dříve ukázali, že (viz. 5.8)
 |
Průběh hustoty pravděpodobnosti složky rychlosti je pro několik teplot zakreslen na obr. 5-3. Průběh odpovídá molekulám vodíku H2.
 Obr. 5-3
Obr. 5-3
Směr pohybu molekuly nás obvykle příliš nezajímá, chceme znát odpověd na otázku, jaká je pravděpodobnost, že velikost rychlosti bude z intervalu (v, v + dv).
Koncové body vektoru rychlosti vyplňují v tomto případě kulovou slupku o poloměru v a tloušťce dv. Její objem je 2nv2 dv. Hustota pravděpodobnosti
 je určena druhou mocninou rychlosti molekuly
je určena druhou mocninou rychlosti molekuly
 . Nevzniknou proto potíže, nahradíme-li elementární objem dvx, dvy, dvz, vyjádřený v pravoúhlých souřadnicích, elementárním objemem
. Nevzniknou proto potíže, nahradíme-li elementární objem dvx, dvy, dvz, vyjádřený v pravoúhlých souřadnicích, elementárním objemem
 vyjádřeným ve sférických souřadnicích. Hustota pravděpodobnosti, že molekula má rychlost z intervalu (v, v + dv), pak určuje výraz
vyjádřeným ve sférických souřadnicích. Hustota pravděpodobnosti, že molekula má rychlost z intervalu (v, v + dv), pak určuje výraz
 |
(5.62) |
Výraz představuje Maxwellovo-Boltzmannovo rozdělení rychlostí molekul.
Díky předexponenciálnímu členu, obsahujícímu v2, je hustota pravděpodobnosti pro v = 0 rovna nule. Molekuly nemohou mít zápornou velikost rychlosti, takže
 i pro v < 0. Hustota pravděpodobnosti je v tomto případě funkce nesymetrická. Její průběh je zakreslen na obr. 5-9. Měřítka na osách byla zvolena tak, že vynesená závislost odpovídá dusíku při teplotách vyznačených jako parametr u jednotlivých křivek.
i pro v < 0. Hustota pravděpodobnosti je v tomto případě funkce nesymetrická. Její průběh je zakreslen na obr. 5-9. Měřítka na osách byla zvolena tak, že vynesená závislost odpovídá dusíku při teplotách vyznačených jako parametr u jednotlivých křivek.
 Obr. 5-9
Obr. 5-9
Maximum křivek odpovídá nejpravděpodobnější hodnotě rychlosti v . Vzhledem k nesymetrii křivek není nejpravděpodobnější rychlost totožná se střední rychlostí. Stanovíme ji jako maximum funkce (5.62). V maximu musí být derivace
 nulová, tedy
nulová, tedy
 |
 |
(5.63) |
V maximu nabývá hustota pravděpodobnosti hodnoty
 |
(5.64) |
Další veličinou charakterizující rozdělení rychlostí je střední rychlost
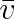 . Podle definice (5.7b) bude
. Podle definice (5.7b) bude
 |
Tento integrál je roven záporně vzaté derivaci integrálu
 |
podle parametru
 . Předchozí integrál není obtížný spočítat, prove-deme-li substituci
. Předchozí integrál není obtížný spočítat, prove-deme-li substituci
 . Protože
. Protože
 , bude
, bude
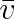 dáno výrazem
dáno výrazem
 |
(5.65) |