 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
a) Izochorický děj (V = konst.). Dodáme-li plynu teplo
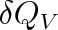, zvýší se jeho teplota o dT. Je-li CV tepelná kapacita plynu stálého objemu, je podle (3.9)
 |
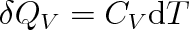(3.22) |
Dosazením (3.22) do (3.21), přičemž dV = 0, dostaneme
 |
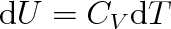(3.23) |
a současně
 |
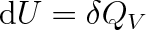(3.24) |
Po integraci (CV pokládáme za konstantu) obou rovnic obdržíme vztah
 |
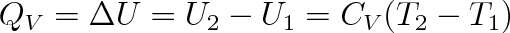(3.24a) |
kde T1 je počáteční a T2 konečná teplota plynu.
Teplo přijaté ideálním plynem při izochorickém ději se rovná přírůstku jeho vnitřní energie. Zvýšení vnitřní energie se projeví zvýšením teploty plynu, kterému odpovídá zvýšení tlaku (viz Charlesův zákon).
Integrujeme-li znovu rovnici (3.23), dostaneme že
 |
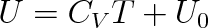(3.25) |
kde U0 je integrační konstanta. Pro T = 0 K je U0 = U. Položíme-li tuto hodnotu rovnou nule (na základě poznatků kinetické teorie plynů, viz 5. kapitola), můžeme říci, že:
Vnitřní energie ideálního plynu je přímo úměrná termodynamické teplotě plynu. Tato formulace je někdy označována jako termodynamická definice ideálního plynu.
Ze vztahu (3.25) také vyplývá, že vnitřní energie ideálního plynu nezávisí na objemu. To ale znamená, že můžeme první termodynamický zákon nyní zapsat
 |
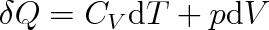(3.26) |
b) Izobarický děj (p = konst). Teplo Qp které musíme dodat plynu, aby při stálém tlaku zvýšil teplotu z Tl na T2 a zvětšil svůj objem z hodnoty Vl na V2, získáme integrací rovnice (3.26) v příslušných mezích. Takže
 |
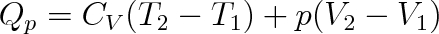(3.27) |
kde člen CV(T2-T1) na pravé straně je roven zvýšení vnitřní energie plynu o
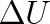a člen p(V2-V1) vyjadřuje práci vykonanou plynem proti vnějším silám.
Teplo přijaté ideálním plynem při izobarickém ději se rovná součtu přírůstku jeho vnitřní energie a práce, kterou plyn vykonal.
V souvislosti se změnami stavu plynu při izobarickém ději je účelné zavést další stavovou funkci. Za tím účelem rovnici (3.21)
 |
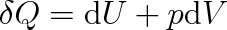upravíme na tvar
 |
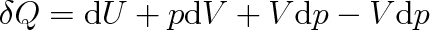Vyjádříme-li výraz p dV + V dp jako diferenciál d(pV), můžeme předchozí rovnici přepsat do tvaru
 |
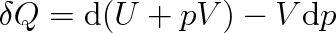Zavedeme-li stavovou funkci entalpie H definicí
 |
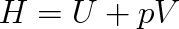(3.28) |
pak předchozí vztah přepíšeme na tvar
 |
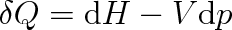(3.29) |
Pro elementární teplo
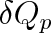izobarický dodané plynu (dp = 0) pak platí
 |
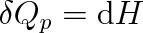(3.30) |
a odtud
 |
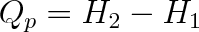(3.30a) |
kde H1 a H2 značí entalpii na počátku a na konci izobarického děje.
Teplo přijaté ideálním plynem při izobarickém ději se rovná přírůstku jeho entalpie.
Entalpie má pro izobarické děje stejný význam jako vnitřní energie pro děje izochorické. Svědčí o tom vztahy (3.30) a (3.30a), které jsou analogické vztahům (3.24) a (3.24a). Úzká analogie se projevuje i ve vztahu uvažovaných stavových funkcí U, H k tepelným kapacitám CV a Cp. Pro izobarický děj s ideálním plynem platí podle (3.30) a (3.9) vztah
 |
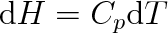(3.31) |
z něhož integrací získáme pro entalpii ideálního plynu výraz (pro T0 = 0 K)
 |
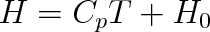(3.32) |
kde H0 je integrační konstanta s významem počáteční hodnoty entalpie. Tuto konstantu sice nedovedeme zjistit, ale protože nás zajímají pouze změny entalpie spojené s přechodem soustavy z jednoho stavu do druhého, není znalost konstanty H0 nutná.
c) Izotermický děj (T = konst.). Protože vnitřní energie ideálního plynu je pouze funkcí termodynamické teploty, je dU = 0. První termodynamický zákon má jednoduchý tvar
 |
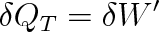kde
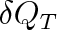je elementární teplo dodané izotermický plynu a
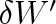elementární práce vykonaná plynem. Integrací dostaneme
 |
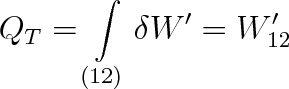(3.33) |
Teplo přijaté ideálním plynem při izotermickém ději je rovno práci, kterou plyn vykonal, aniž přitom změnil svou vnitřní energii. Pro elementární práci vykonanou plynem platí
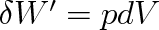, takže
 |
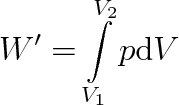(3.34) |
kde V1 a V2 je počáteční a konečný objem plynu při izotermickém ději. Protože
při tomto ději je p = p(V), dosadíme za p ve vztahu (3.34) ze stavové rovnice (2.16). Pro celkovou práci W vykonanou plynem dostaneme vztah
 |
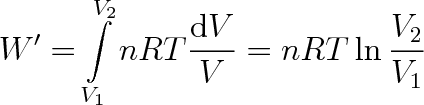(3.35) |
Při izotermické kompresi je Vl > V2 , což znamená W < 0, neboli W > 0. V tomto případě konají vnější síly na plynu práci W a plyn odevzdává do okolí stejně velké teplo Q'T .
d) Adiabatický děj (
) se uskutečňuje s plynem, který ani nepřijímá ani neodevzdává teplo. První termodynamický zákon zapíšeme pro tento děj ve tvaru
 |
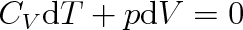a ponecháme v něm jen dvě proměnné stavové veličiny, např. p a V. To vyžaduje za dT dosadit z diferencované stavové rovnice (2.16) výraz (p dV + V dp)/nR. Po úpravě dostaneme rovnici
 |
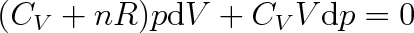Položíme-li podle (3.14) CV + nR = Cp a násobíme-li rovnici výrazem 1/pV, dostaneme
 |
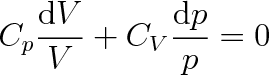Zavedeme-li do této rovnice ještě Poissonovu konstantu
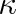podle (3.20), přejde předchozí rovnice do tvaru
 |
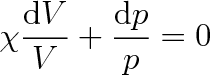Integrací této rovnice dostaneme
 |
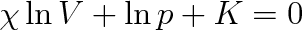Písmenem K je označena celková integrační konstanta. Tuto rovnici můžeme po jednoduché úpravě napsat ve tvaru
 |
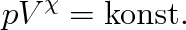(3.36) |
Dostali jsme matematický zápis Poissonova zákona, který udává závislost tlaku ideálního plynu na jeho objemu při adiabatickém ději. Rovnice (3.36) se také nazývá rovnicí adiabaty .
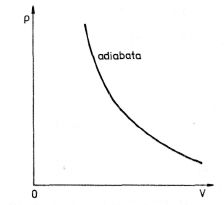Obr. 3-5
Při izotermickém ději je nutný dokonalý styk plynu s okolím (ohřívačem), při adiabatickém ději musí být naopak plyn dokonale tepelně izolován od okolí. Skutečné děje, které nazývá polytropické děje, probíhají mezi dějem adiabatic-kým a dějem izotermickým.
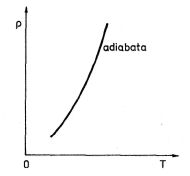Obr. 3-7
Tepelný kontakt zkoumaného plynu s okolím (ohřívačem) charakterizuje tepelná kapacita C, o které při polytropickém ději předpokládáme, že je konstantní.
Závislost stavových veličin p, V pro polytropický děj udává rovnice
 |
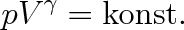(3.40) |
kde gamma je tzv. polytropický koeficient. Jeho hodnota leží v intervalu (1,
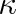) neboť je definován výrazem
 |
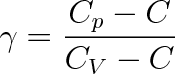(3.41) |
Grafem (3.40) je polytropa. Na obr. 3-8 představuje vyšrafovaná plocha soubor polytrop s
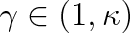. S použitím stavové rovnice ideálního plynu získáme polytropy v diagramech (V,T) a (T, p)
.
 |
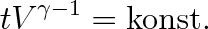(3.42) |
 |
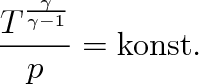(3.43) |
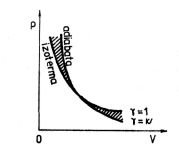Obr. 3-8
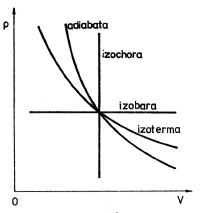Obr. 3-9b
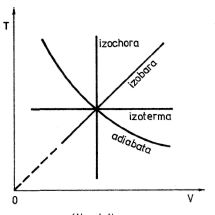Obr. 3-9a
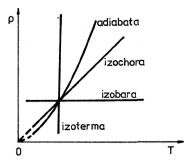Obr. 3-9c
|
|
|
|
|
|
|
|
|