Uvažujme termodynamicky homogenní soustavu ve stavu termodynamické rovnováhy. Stav této soustavy lze popsat tím, že udáme teplotu T a množinu x1, x2 . . . , xn vnějších parametrů charakterizujících vnější podmínky, v nichž se soustava nachází. Všechny vnitřní parametry yi charakterizující danou soustavu je možno vyjádřit pomocí stavových proměnných T, x1 ,x2 . . . , xn. Funkci ve tvaru
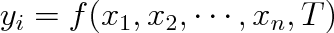 |
(2.13) |
nazýváme stavovou rovnicí termodynamicky homogenní soustavy ve stavu termodynamické rovnováhy.
Termodynamika určuje stavovou rovnici experimentálně. Teoretickým odvozením této rovnice se zabývá statistická fyzika.
Nejjednodušší tvar má stavová rovnice pro ideální plyn. Z hlediska kinetické teorie látek vyslovujeme o molekulách ideálního plynu následující předpoklady:
Molekuly určitého ideálního plynu (např. H2) mají všechny stejnou hmotnost.
Molekuly daného ideálního plynu mají kulový tvar, poloměr všech molekul je stejný (řádově 10-10 m). Přitom objem molekul ideálního plynu je zanedbatelný proti objemu, který plyn zaujímá.
Povrch molekul je dokonale hladký, takže tření při srážkách je nulové.
Při všech srážkách mezi sebou i se stěnami nádoby se molekuly chovají jako dokonale pružné, tj. splňují princip zachování energie a princip zachování hybnosti (celková energie a celková hybnost molekul podílejících se na srážce se při srážce nezmění).
Mimo okamžiky srážek na sebe molekuly ideálního plynu nepůsobí navzájem silami.
V době mezi vzájemnými srážkami a nárazy na stěnu se molekuly pohybují rovnoměrným přímočarým pohybem.
Zdůvodnění tohoto zjednodušeného modelu plynu je jediné - jeho úspěch. Experimenty potvrdily, že reálný plyn, ačkoliv má složité molekuly, se v mnoha případech chová jako ideální plyn. Je tomu tak při dostatečně vysokých teplotách a nízkých tlacích. Např. při normálních podmínkách lze většinu plynů s dostatečným stupněm přesnosti považovat za ideální plyny.
Vyslovené předpoklady o ideálním plynu (viz též čl. 5.1) umožňují vyslovit další jeho vlastnost: Poněvadž molekuly ideálního plynu nepůsobí na sebe navzájem silami (s výjimkou velmi krátkých okamžků jejich vzájemných srážek), je celková potenciální energie soustavy molekul ideálního plynu nulová (E = 0). Proto podle vztahu (2,2) je vnitřní energie ideálního plynu rovna celkové kinetické energii tepelného pohybu molekul (U = Ek). Jedná-li se o ideální plyn s jednoa-tomovými molekulami, je jeho vnitřní energie rovna součtu kinetických energií molekul pohybujících se neuspořádaným posuvným pohybem. Vnitřní energie ideálního plynu s víceatomovými molekulami zahrnuje kromě toho ještě energii rotační a vibrační (podrobněji viz čl. 5.7).
Ideální plyn je jednoduchou homogenní termodynamickou soustavou. Vnější parametr stačí zvolit jediný, a to objem plynu V, vnitřním parametrem je tlak p plynu. Potom stavová rovnice (2.13) je určena závislostí
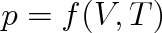 |
(2.14) |
Tvar této závislosti můžeme zjistit experimentálně .
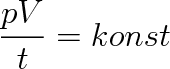 |
(2.15) |
Při stavové změně ideálního plynu stálé hmotnosti zůstává výraz pV/T konstantní.
Zjistíme-li hodnoty p, V, T pro libovolně zvolený rovnovážný stav plynu, můžeme ze stavové rovnice (2.15) vypočítat hodnotu konstanty. Zvolíme-li tímto stavem normální podmínky, při nichž p0 = 101 325 Pa a T0 = 273, 15 K a plyn bude mít látkové množství 1 mol, pak podle (1.11) je objem plynu Vmn — = 22,414 . 1(T-3 m3 . mol-1. To znamená, že konstanta z rovnice (2.15) má hodnotu
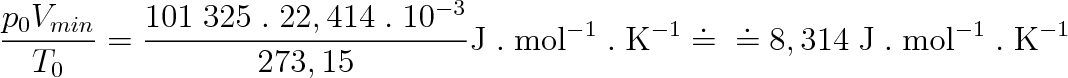 |
Konstanta R = 8,314 J . mol-1 . K-1 je pro všechny ideální plyny stejná a nazývá se molární plynová konstanta .
Pomocí této konstanty dostáváme :
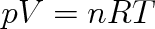 |
(2.16) |
Ze stavové rovnice dostáváme také vztahy pro případy, že jedna ze stavových veličin p, V, T zůstává konstantní při změně stavu ideálního plynu stálé hmotnosti. Jde o vztahy charakterizující 3 jednoduché děje :