---

---

1.3 Tečné a normálové zrychlení

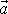Zrychlení bodu je možno rozložit na složku do směru rychlosti, kterou nazýváme  tečná složka zrychlení nebo stručně tečné zrychlení 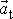, a na složku kolmou ke směru rychlosti, kterou nazýváme normálové zrychlení .

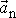Průmět a;a_v vektoru 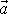do směru rychlosti získáme, vynásobíme-li skalárně vektor 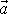jednotkovým vektorem 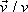ve směru a smyslu rychlosti bodu;

.

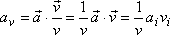(1,15)

Výraz a_iv_i v poslední úpravě rovnice (1,15) je vyjádření skalárního součinu vektoru zrychlení  a_i a vektoru rychlosti v_i ve složkové symbolice  (viz dodatek D.1). Ve složkové symbolice se užívá sčítací (sumační) pravidlo, dle kterého, vyskytuje-li se v součinu dvakrát stejný index, sčítá se přes něj. Výraz a_iv_i   symbolizuje součet součinů jednotlivých složek násobených vektorů tedy jejich skalární součin;

.

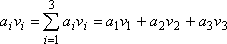Známe-li průmět  a_v zrychlení do směru rychlosti, získáme tečnou složku 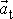zrychlení vynásobením průmětu a_v jednotkovým vektorem 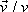ve směru a smyslu vektoru rychlosti;

.

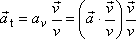(1,16)

Stejný   vzorec napsaný ve složkové symbolice má tvar

.

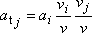(1,16´)

Výraz a_v  z rovnice (1,15) souvisí s velikostí a_t tečného zrychlení 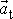jednoduchým vztahem a_v = ąa_t , kde kladné znaménko platí, je-li vektor 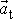souhlasně rovnoběžný (má stejný směr a smysl neboli stejnou orientaci) s vektorem 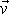, záporné znaménko platí pro nesouhlasně rovnoběžné vektory 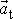a .

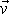Zrychlení 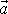je součtem tečného 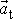a normálového zrychlení 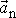; 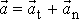. Ze známých hodnot 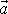a (viz rov. (1,16) ) můžeme pak normálové zrychlení stanovit jako

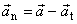(1,17)

nebo ve složkové symbolice

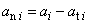(1,17´)

Tečné zrychlení charakterizuje změnu velikosti rychlosti s časem. Pro veličinu a_v = ą a_t , která udává hodnotu vektoru  tečného zrychlení 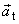 v přímce jeho působení (přímka proložená vektorem rychlosti a orientovaná souhlasně s ním), platí vztah

.

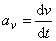(1,18)

Tečné zrychlení je rovno časové derivaci velikosti rychlosti. Stoupá-li velikost rychlosti, je tečné zrychlení orientováno souhlasně se směrem rychlosti bodu, klesá-li velikost rychlosti, jsou orientace tečného zrychlení a rychlosti opačné.

Podáme důkaz tvrzení (1,18) .

Velikost rychlosti 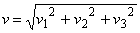, jejím derivováním dostaneme

.

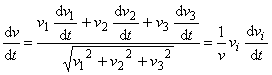Jelikož 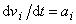, lze shora uvedený výraz pro dv/dt přepsat na tvar

,

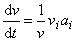jehož pravá strana je totožná s pravou stranou rovnice (1,15) . Tedy derivace velikosti rychlosti  dv/dt   se rovná průmětu  a_v  vektoru 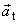  do směru rychlosti bodu; a_v= dv/dt . Tím je důkaz tvrzení (1,18) proveden.

Velikost normálového zrychlení  a_n   souvisí se zakřivením dráhy pohybu. Platí rovnice

,

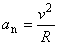(1,19)

kde  R   je poloměr oskulační kružnice dráhy bodu a  v  velikost rychlosti bodu v místě, pro které je určena hodnota  a_n .

Důkaz tvrzení (1,19) zde nemá smysl provádět, protože běžnému čtenáři nebude znám pojem oskulační kružnice (viz např. [24], str.263). Rovnici (1,19) může čtenář pokládat za definiční rovnici poloměru  R , případně se může spokojit s intuitivním tvrzením, že oskulační kružnice je taková kružnice, která se v daném bodě ze všech kružnic nejlépe přimyká k dráze bodu. Je-li drahou bodu kružnice, musí poloměr této kružnice být současně poloměrem oskulační kružnice. Pro pohyb po kružnici můžeme potom pravdivost tvrzení (1,19) ověřit, což provedeme v následujícím článku při rozboru nerovnoměrného kruhového pohybu (viz rov. (1,45) ).

---

---