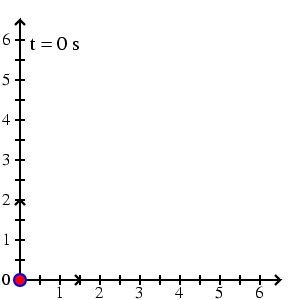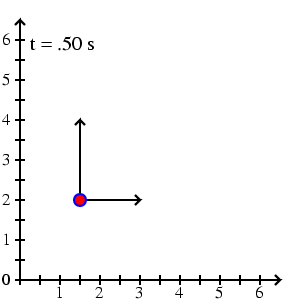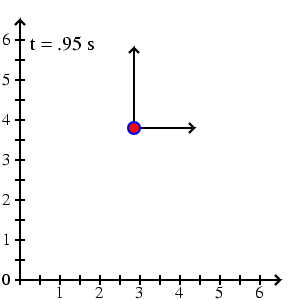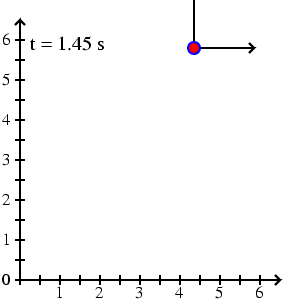
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Pohyb bodu se v mechanice zpravidla popisuje tak, že zvolíme soustavu souřadnic pevně spjatou s nějakými tělesy v okolí pohybujícího se bodu a sledujeme, jak se v této soustavě souřadné mění souřadnice bodu s časem. V trojrozměrném prostoru tak získáme tři funkce f1(t), f2(t), f3(t), které udávají, jak se jednotlivé souřadnice bodu mění s časem t. Pro nejčastěji užívané kartézské souřadnice tak dostáváme vyjádření
 . |
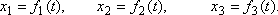(1,1) |
Funkce f1(t),f2(t), f3(t) tak udávají časový průběh průmětů hmotného bodu do třech vzájemně kolmých směrů, v kterých leží kartézské souřadnicové osy. Ve fyzice bývá zvykem pro funkční znak psát stejný symbol jako pro příslušnou veličinu, a tedy rovnice (1,1) psát v tvaru
 . |
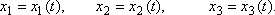(1,2) |
Z geometrie je známo (např. [24], kap.9), že rovnice (1,1) za jistých pro běžné pohyby obvykle splněných předpokladů kladených na funkce f1,f2,f3 popisují parametricky křivku. V mechanice přebíráme tento parametrický popis křivky. Parametr t však není libovolný, ale má přesný fyzikální význam: znamená čas.
Rovnice (1,2) , které kinematicky popisují pohyb bodu, nazýváme parametrickými rovnicemi pohybu bodu. Rovnice (1,2) popisují trajektorii pohybu bodu, tj. dráhu s uvážením času, v kterém se bod v určitém místě dráhy nachází. Zajímá-li nás tvar dráhy, po které se bod pohybuje, určíme jej vyloučením parametru t z rovnic (1,2) . Užijeme-li složkové symboliky (viz dodatek D.1), je možné rovnice (1,2) stručně zapsat jako
 . |
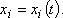(1,3) |
V mechanice bývá zvykem tři souřadnice xi bodu
pokládat za složky vektoru, pro který užíváme označení
a nazýváme jej polohovým vektorem bodu. Vektor
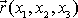můžeme geometricky znázornit orientovanou
úsečkou s počátkem v počátku souřadnicové soustavy a koncem
v místě, kde se nachází hmotný bod.
Pevné umístění počátku vektoru není ve shodě s matematickým pojmem vektor. Proto se pro takový vektor někdy zavádí (např. [ 14 ] , str. 100) označení umístěný vektor. U pojmu vektor obvykle vyšetřovaného v matematice na umístění počátku nezáleží ; dva vektory jsou shodné, když mají stejnou velikost a směr. Matematický vektor pak nazveme volný vektor.
V symbolice užívající polohového vektoru
lze rovnice
(1,2)
, resp.
(1,3)
psát ve tvaru
 . |
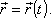(1,4) |
Pohyb daný parametrickými rovnicemi
 |
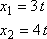(1,5) |
je pohybem po přímce
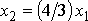(viz obr.1). Pohyb
 |
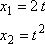(1,6) |
se koná po parabole o rovnici
. Na obr.2, na kterém je pohyb znázorněn, jsou stejně jako na obr.1 uvedeny časy,
v kterých se bod nachází v jednotlivých bodech dráhy. Úsek mezi
čárkami na osách odpovídá délkové jednotce.
|
|
|
|
|
|
|
|
|