---

---

2.3 Časová závislost vztahu deformace a napětí, viskoelastické látky

Ostrý přechod mezi kapalnou a pevnou fází nastává pouze pro jednoduché nízkomolekulární látky, které v pevné fázi vytvářejí pravidelnou krystalickou strukturu (viz např. [5], kap. 10). Avšak ani pro takové látky z reologického hlediska hranice mezi kapalinou a pevnou látkou není zcela ostrá. Např. voda při rychle probíhajících dějích vykazuje elastické vlastnosti, o čemž se můžeme nemile přesvědčit, skočíme-li do ní nešikovně z větší výšky, a led při dlouhodobém působení vnější síly trvale mění svůj tvar. Látky se složitější molekulární strukturou, jakými jsou různá skla, kaučuky, plastické hmoty, laky, asfalty, malty apod., nemají ostrý přechod mezi kapalnou a pevnou fází ani z termodynamického hlediska (viz zmínka o amorfních látkách v [5], čl. 10.1).

Pro reologický popis látek, které leží na pomezí mezi kapalinami a pevnými látkami, je nutno zavést modely kombinující vlastnosti obou druhů látek. Nejjednodušším takovým modelem je model lineární viskoelastické látky, který vznikne kombinací vlastností newtonovské viskózní kapaliny a hookovské elastické látky. Pro větší názornost přiřazujeme modelům reologických látek grafické symboly, jak jsme se o tom již zmínili při zavedení modelu hookovské a newtonovské látky. Vztah mezi napětím a deformací hookovské látky (rov. (2,46) a obr.22) je stejný jako vztah mezi silou protahující kovovou pružinu a relativním prodloužením této pružiny. Proto chování hookovské látky symbolizujeme spirálovou pružinou, pro níž užíváme grafický symbol znázorněný na obr.29a). Chování newtonovské látky se vystihuje pístem pohybujícím se ve viskózní kapalině; užívané symbolické označení pístu je znázorněno na obr.29b). Předpokládá se, že rychlost pohybu pístu je přímo úměrná síle na něj působící, což je závislost odpovídající vztahu mezi rychlostí deformace a napětím newtonovské látky (viz rov (2,52) a obr.27).

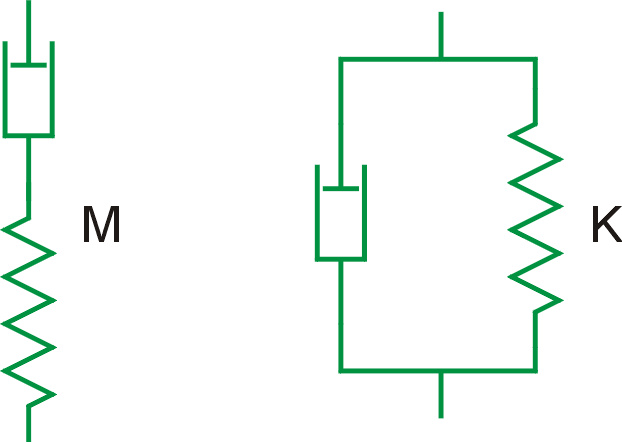Nejjednodušší modely visko-elastických látek získáme, spojíme-li sériově nebo paralelně modely hookovské a newtonovské látky. Tak vznikne model Maxwellův znázorněný na obr.30 a model Kelvinův (užívá se pro něj též názvu Voigtův) znázorněný na obr.31. Hookovskou pru-žinu jsme označili písmenem H, newtonovský píst písme-nem N, Maxwellův model M, Kelvinův model K, seriové spojení vodorovnou čarou - a paralelní spojení šikmou čarou /. Pro Maxwellův model M pak můžeme psát stručné označení M = H - N, které ukazuje, jak je model sestaven. Obdobně pro Kelvinův model dostáváme vyjádření K = H /N.

Každému modelu odpovídá reologická rovnice určující časovou závislost vztahu mezi napětím t a deformací g. Pro model hookovské látky H je to přímá úměrnost (2,46)

,

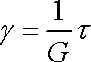(2,46)

pro model newtonovské látky přímá úměrnost mezi časovou derivací deformace a napětím (2,52)

.

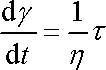(2,52)

Rovnice H-modelu (2,46) předpokládá, že deformace úměrná napětí se ustavuje v látce okamžitě. Změny deformace bezprostředně sledují změny napětí a naopak změny napětí bezprostředně vyvolávají deformaci. Časová závislost vztahu deformace a napětí vyjádřená rovnicí (2,52) je již složitější. Napětí a deformace mají vztah jako funkce a její derivace. Např. stálé deformaci odpovídá nulové napětí, stálému napětí odpovídá deformace zvětšující se konstantní rychlostí.

Jak získáme reologické rovnice odpovídající Maxwellovu modelu M (obr.30) a Kelvinovu modelu K (obr.31)? Při odvozování reologických rovnic neuvažujeme ani délku ani příčné rozměry jednotlivých částí modelu. Přiřazujeme-li dvěma částem modelu spojeným sériově deformace a , předpokládáme, že celému modelu přísluší deformace . Při sériovém spojení částí modelu pokládáme napětí t za stejné v celém modelu; . Při paralelním spojení předpokládáme, že napětí a působící v jednotlivých částech modelu se sčítají; a deformaci v obou částech modelu pokládáme za stejnou; .

Maxwellův model vznikne sériovým spojením Hookova členu H, pro jehož deformaci z rovnice (2,46) plyne

,

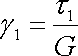(2,55)

s Newtonovým členem N, pro nějž dle (2,52)

.

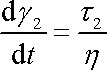(2,56)

Dle právě vyložených pravidel sériového spojování modelů platí

.

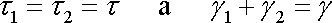(2,57)

Abychom mohli využít pravidlo o sčítání deformací, musíme nejprve zderivovat rovnici (2,55) dle času t, dostáváme

.

(2,58)

Derivace součtu se rovná součtu derivací, a tedy

,

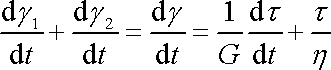když dle první z rovnic (2,57) napětí a označíme společnou hodnotou t.

Rovnice

(2,59)

je hledaná reologická rovnice Maxwellova modelu.

Reologickou rovnici Kelvinova modelu (obr.31) získáme, když na rovnice (2,46) a (2,52) aplikujeme pravidla pro paralelní spojování částí modelů: a . Vynásobíme-li rovnici (2,46) modulem pružnosti ve smyku G a rovnici (2,52) viskozitou h a obě rovnice sečteme, dostaneme

.

(2,60)

Rovnice (2,60) je reologická rovnice Kelvinova modelu.

Dle reologické rovnice zjistíme průběh jedné z veličin t nebo g, známe-li časovou závislost druhé. Je-li např. zadán časový průběh deformace pro látku popsanou Maxwellovým modelem, zderivujeme tuto závislost a získáme levou stranu rovnice (2,59) , kterou označíme . Rovnice (2,59) je pak diferenciální rovnicí

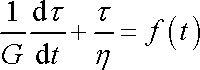(2,61)

pro neznámý průběh napětí. Při konstantní deformaci je a rovnice (2,61) je homogenní diferenciální rovnicí prvního řádu s konstantními koeficienty pro neznámou funkci ;

.

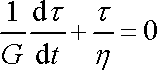(2,62)

Řešením rovnice (2,62) je (srov. např. s rov. (I4,24)) průběh napětí daný rovnicí

,

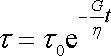(2,63)

kde je napětí v čase t = 0. Předpokládáme-li, že deformace byla vzorku v čase t = 0 udělena skokem, je . Je-li maxwellovská látka trvale deformována ( 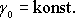), napětí v ní klesá s časem; mluvíme o relaxaci napětí[+]. Pro látku, jejíž reologické chování je popsáno Maxwellovým modelem, je relaxace napětí přesně exponenciální vyjádřená rovnicí (2,63) .

Působí-li na Maxwellův model stálé napětí , dostáváme po dosazení do rovnice (2,59)

,

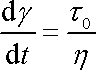a tedy

.

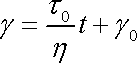Deformace je deformace v čase t = 0. Tato deformace, které říkáme okamžitá, je dána Hookovým členem Maxwellova modelu. Její velikost je tedy a pro celkovou deformaci g při stálém napětí dostáváme konečné vyjádření

.

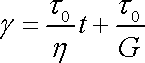(2,64)

Vzorek se okamžitě deformuje a poté rovnoměrně zvyšuje svou deformaci s časem. Časový průběh deformace je znázorněn v části a) obr.32 (počátek děje je posunut z času t = 0 do času t = ). Časovou závislost deformace při konstantní hodnotě napětí nazýváme tečením nebo též creepem (krípem). Tečení popsané rovnicí (2,64) s rostoucím časem neomezeně roste. Látka popsaná Maxwellovým modelem vykazuje při creepu okamžitou deformaci a neomezené tečení stálou rychlostí.

Creepové chování řady viskoelastických látek vystihuje Kelvinův model (obr.31). Vyšetříme, jak Kelvinův model popisuje creep, to znamená, že vypočteme jakou časovou závislost deformace model udává, aplikujeme-li na něj stálé napětí . Reologická rovnice modelu (2,60) v tomto případě zní

.

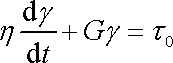(2,65)

Je to lineární diferenciální rovnice prvního řádu s konstantními koeficienty a nenulovou pravou stranou. Jejím řešením je součet obecného řešení rovnice homogenní (s nulou na pravé straně) a jednoho řešení rovnice nehomogenní, tj. celé rovnice i s nenulovou pravou stranou (srov. I, rov. (I4,118) a následující text). Řešení homogenní rovnice je analogické řešení (2,63) rov. (2,62) , tedy

.

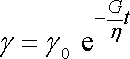(2,66)

Jedno řešení celé rovnice (2,65) dostaneme, když deformaci g položíme rovnu konstantě k, pro jejíž velikost z rovnice (2,65) plyne

.

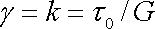(2,67)

Sečtením (2,66) a (2,67) dostáváme obecné řešení rovnice (2,65)

.

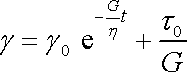(2,68)

Pro přirozenou počáteční podmínku plyne z (2,68) a hledaný časový průběh creepu pro Kelvinův model probíhá tedy dle rovnice

.

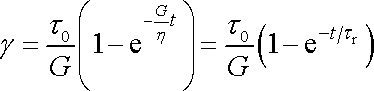(2,69)

Průběh funkce (2,69) je znázorněn na obr.32d). Deformace se v průběhu času (v obr. je počátek děje označen , ne 0 ) exponenciálně blíží své mezní hodnotě , tj. hodnotě, kdy pružina modelu kompenzuje působící napětí . V druhém vyjádření g na pravé straně rovnice (2,69) je zavedena relaxační doba , tj. čas, za který se creep přiblíží na jednu e-tinu ke své mezní hodnotě (srov. I, rov. (I4,113) ). Vyjádření vlastností viskoelastické látky dle relaxačních dob procesů, které v ní probíhají, je typické nejen pro viskoelasticitu, ale i pro další relaxační děje (viz pozn. pod čarou na str. 58).

V obr. 32 je creepové chování Maxwellova a Kelvinova modelu doplněno v části b) a c) creepovým chováním dvou poněkud složitějších modelů. Čtyři modely z obr.32 vystihují základní rysy chování čtyř typů viskoelastických látek. Při creepu se tyto typy liší tím, zda existuje okamžitá deformace a zda existuje neomezené tečení. Okamžitá deformace nastává u modelů z obr.32a) a 32b), neomezené tečení u modelů z obr.32a) a 32c), Kelvinův model (obr. 32d)) nevykazuje ani okamžitou deformaci ani neomezené tečení.

Všechny uvažované modely vystihují pouze základní charakter chování viskoelastických látek. Lze např. těžko předpokládat, že creep u skutečné látky bude probíhat přesně podle křivky znázorněné na obr.32a). Je-li však creep skutečné látky dán křivkou znázorněnou na obr. 33, jeho základní rysy jsou vystiženy hrubým modelem z obr.32a). Stejně tak pro málokterou reálnou látku relaxace napětí bude mít přesně exponenciální průběh daný rovnicí (2,63) , ale u řady látek bude napětí s časem postupně relaxovat od původní hodnoty až po hodnotu nulovou, což je typ relaxační závislosti vystižený Maxwellovým modelem.

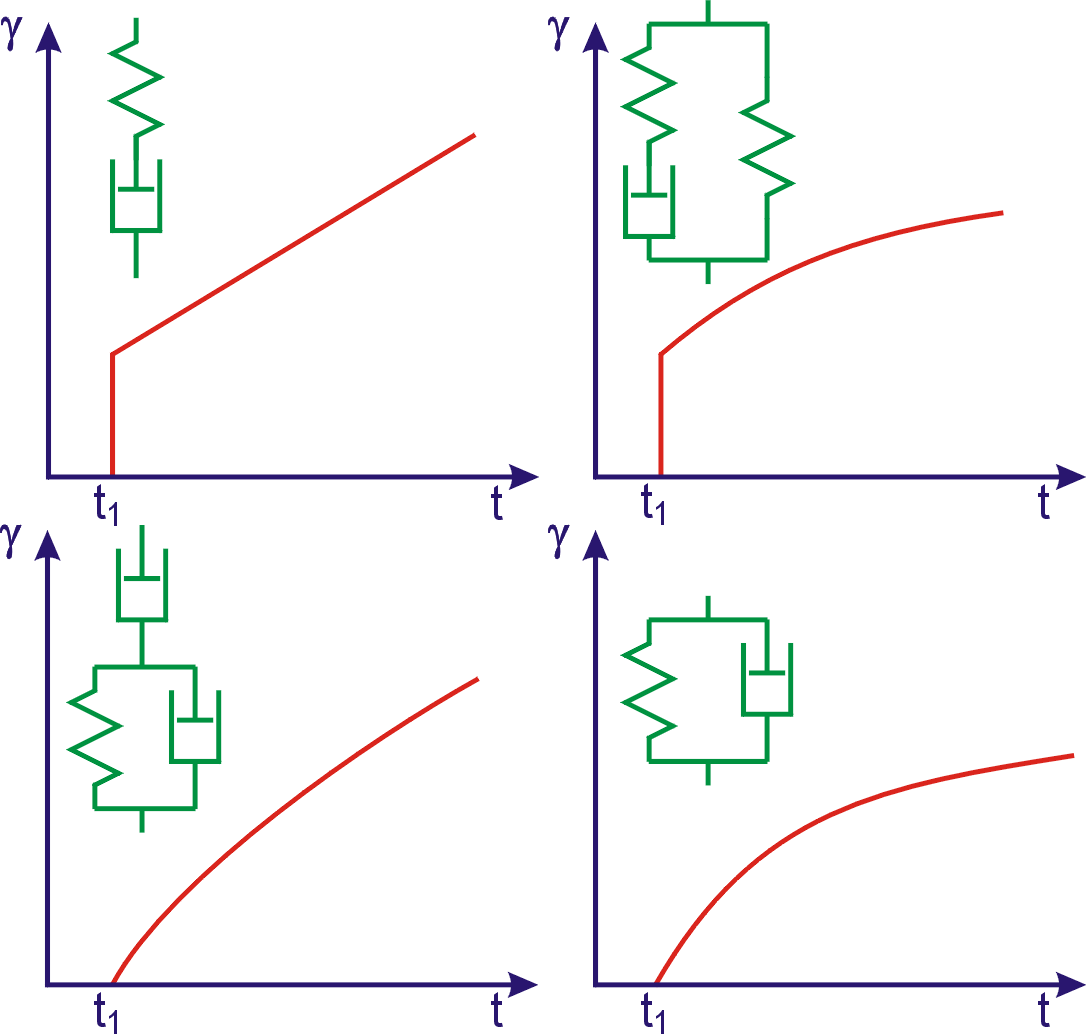
Obr. 32

V základních reologických modelech je látka charakterizována několika málo konstantami. V modelech na obr.32 jsou to dvě až tři konstanty. Chceme-li přesněji vystihnout chování reálné viskoelastické látky, musíme zvýšit počet konstant, kterými toto chování popisujeme.

Místo jednoduchých modelů užíváme modelů s více členy, např. modelu znázorněného na obr.34, který spojuje sériově několik Kelvinových ( v obrázku je počet označen číslem N ) a jeden Maxwellův model. Reologická rovnice odpovídající modelu z obr.34 je složitější než rovnice (2,59) nebo (2,60) a pro větší čísla N je obtížně řešitelná.

 

Viskoelasticitu není nutno budovat na základě modelů. Pro chování viskoelastické látky je charakteristický průběh vzájemného poměru napětí a deformace při různých druzích namáhání. Známe-li např. časový průběh 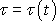napětí v látce při stálé deformaci , tj. známe-li relaxaci napětí ve vzorku, tento průběh látku viskoelasticky charakterizuje a průběh vztahu napětí a deformace při jiných druzích namáhání vzorku vypočteme integrálními transformacemi funkce . Takto budovaná teorie viskoelasticity se nazývá nemodelová a je popsána např. v [20], [24]. Zajímavé jsou analogie mezi teorií viskoelasticity a teorií elektrických sítí (viz např. [25], kap. 5, [42] ). Obojí totiž, omezíme-li se na lineární oblast, spadají pod obecnou teorii lineární odezvy.

 

Podobně jako teorie pružnosti (viz kap. 3) zkoumá namáhání hookovské látky při složitém geometrickém rozložení působících sil, je možno i pro viskoelastické látky zkoumat časový průběh namáhání pro složitější geometrické rozložení sil působících na vzorek, tedy pro případ dvou i trojrozměrného namáhání (viz např. [26] ).

 

Viskoelasticita vybudovaná na základě Hookova modelu H a Newtonova modelu N, stejně jako výše zmíněná nemodelová teorie, jsou teoriemi lineárními; mluvíme o lineární viskoelasticitě. Při daném druhu namáhání látky předpokládáme, že n-krát větší hodnota napětí způsobí ve stejném čase t n-krát větší hodnotu deformace a naopak n-krát větší deformace vyvolá n-krát větší napětí. Ani tento předpoklad nebývá často pro reálné látky splněn, zvláště jedná-li se o větší namáhání. K vystižení nelineárního chování viskoelastických látek se budují nelineární teorie viskoelastického chování (viz např. [20] ). Jsou to však matematicky složité teorie, do kterých se jen obtížně dosazují výstižné fyzikální charakteristiky zkoumaných materiálů. Proto experimentálních výsledků, kde zkoumaná látka by byla pokládána za nelineárně viskoelastickou, je málo. Provádí-li se strukturní výzkum viskoelastických látek, deformace se udržují co nejmenší, aby podmínky lineárně viskoelastického chování byly zachovány.

 

---

---