V příkladech 3.4.6a a 3.4.6b byla demonstrována souvislost mezi magnetickým dipólovým momentem a momentem hybnosti pro nabitou částici konající rovnoměrný kruhový pohyb a pro rotující nabitou kouli. Pro uvedené soustavy byla zavedena veličina zvaná gyromagnetický poměr. Experimentální zkušenost ukazuje, že vztah mezi těmito veličinami má hlubší fyzikální význam. Často totiž nastává situace, kdy daná magneticky aktivní soustava vytvářející magnetické pole, jež je možné popsat polem magnetického dipólu m , má rovněž určitý moment hybnosti L , přičemž mezi oběma momenty platí přímá úměrnost
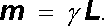 |
(6.36) |
Konstanta úměrnosti se nazývá gyromagnetický poměr a sama soustava se nazývá gyromagnetickou. Vedle makroskopických objektů mohou gyromagnetické vlastnosti jevit i objekty mikroskopické, a to jak elementární částice (například elektron), tak částice složené, například atomy či molekuly - viz článek 7.1.4.
Gyromagnetická částice je ve vnějším magnetickém poli B podrobena silovému působení. Moment síly M působící na částici o magnetickém momentu m je dán vztahem (3.108)

a její pohybová rovnice může být sestavena pomocí 2. impulsové věty, podle níž je časová změna momentu hybnosti rovna momentu vnějších sil. Tedy
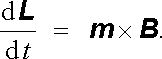 |
(6.37) |
Využitím vztahu (6.36) může být pohybová rovnice vyjádřena jen pomocí mag-netického momentu. Dostaneme tak konečný výsledek
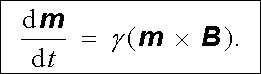 |
(6.38) |
Z tvaru rovnice (6.38) je na první pohled vidět gyroskopické chování částice. Zejména je vidět, že časová změna magnetického momentu d m /dt je vždy kolmá k oběma vektorům m , B . Ve speciálním případě nulového magnetického pole plyne z pohybové rovnice (6.38) m = konst. Magnetický moment je tedy v dané inerciální soustavě nehybný.
Nalezneme řešení pohybové rovnice (6.38) pro případ homogenního, časově neproměnného magnetického pole B 0, které nechť je orientováno v kladném směru osy z kartézské soustavy souřadné S ℜ ≡ (x, y, z), v níž provádíme zkoumání a o níž předpokládáme, že je inerciální. Platí tedy B 0 ℜ ≡ (0, 0, B0).
Hledané řešení lze nejsnáze a nejnázorněji získat přechodem k neinerciální soustavě S ℜ' ℜ ≡ (x ℜ' , y ℜ' , z ℜ' ) rotující konstantní úhlovou rychlostí ω kolem osy z. Pohybovou rovnici (6.38) lze do této soustavy snadno přetransformovat, vezmeme-li v úvahu způsob transformace časové derivace libovolné vektorové funkce času, který je znám z mechaniky (viz například [12]). Označíme-li δ m (t)/ δ t derivaci veličiny m (t) vztaženou k soustavě S ℜ' , platí
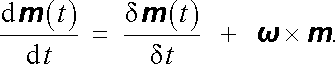 |
Po dosazení do (6.38) můžeme pohybovou rovnici ihned vyjádřit v rotující soustavě S ℜ' . Ponecháme-li obvyklé značení derivace (d/dt ) i v této soustavě, můžeme napsat
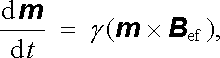 |
(6.39) |
přičemž jsme zavedli efektivní magnetické pole
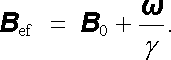 |
(6.40) |
Vidíme tedy, že v rotující soustavě souřadné má pohybová rovnice formálně shodný tvar jako v soustavě inerciální. Rozdíl je pouze v tom, že kromě skutečného pole B 0 v ní vystupuje ještě zdánlivé pole an> /γ . Částice se chová tak, jako kdyby na ni působilo efektivní pole dané vztahem (6.40) .
Na volbu úhlové rychlosti ω nebylo dosud kladeno žádné omezení. Její hodnota může tedy být zcela libovolná a může být určitým způsobem zvolena. Jednoduchá situace nastane, zvolíme-li pro ni hodnotu an> 0, pro niž je B ef = 0 . Tedy
(eq0056) (6.41)
V této speciálně zvolené rotující soustavě souřadné bude mít pohybová rovnice (6.39) triviální tvar a magnetický moment m bude podle článku 6.2.1 v této soustavě nehybný. Předpokládáme-li, že svírá s osou z ℜ' jistý úhel ϑ daný počátečními podmínkami, snadno určíme také pohyb v inerciální soustavě S. Vektor magnetického momentu m bude v této soustavě opisovat kuželovou plochu s vrcholovým úhlem 2ϑ ; bude tedy konat precesní pohyb s úhlovou frekvencí ω 0 danou vztahem (6.41) (viz obr. 6.7). Tento typ pohybu se nazývá Larmorova precese a frekvence ω 0 se nazývá Larmonova frekvence.