---

---

7.4 Metody zjednoduťovåní logických výrazů

7.4.1 Předmět a metody zjednodušování logických výrazů

V tomto odstavci se budeme zabĂ˝vat zjednoduĹĄovĂĄnĂ­m logickĂ˝ch vĂ˝razĹŻ z hlediska co nejmenĹĄĂ­ho počtu logickĂ˝ch členĹŻ, potřebnĂ˝ch k realizaci určitĂŠ logickĂŠ funkce. Toto hledisko je pouŞívĂĄno nejčastěji, neboĹĽ souvisĂ­ s nĂĄklady na realizaci přísluĹĄnĂŠ logickĂŠ funkce. Je vĹĄak třeba si uvědomit, Ĺže zde se budeme zabĂ˝vat pouze realizacĂ­ logickĂ˝ch funkcĂ­ pomocĂ­ hradel zĂĄkladnĂ­ logiky, tj. hradel AND, OR resp. NAND, NOR. V mnoha případech vĹĄak je moĹžnĂŠ poĹžadovanou logickou funkci realizovat pomocĂ­ integrovanĂ˝ch obvodĹŻ střednĂ­ nebo velkĂŠ integrace s nĂĄklady podstatně niŞťími, neĹž by byly nĂĄklady na jejĂ­ realizaci pomocĂ­ hradel zĂĄkladnĂ­ logiky. Představitelem integrovanĂŠho obvodu schopnĂŠho generovat prakticky libovolnou logickou funkci je jednočipovĂ˝ mikropočítač (viz kapitolu 7), k vytvořenĂ­ jednoduĹĄĹĄĂ­ch logickĂ˝ch funkcĂ­ mĹŻĹžeme pouŞít tzv. programovatelnĂĄ logickĂĄ pole (PLA - programable logical array). ProgramovatelnĂŠ logickĂŠ pole reprezentuje prakticky zĂĄpis logickĂŠ funkce v mintermech, tj. jako logickĂ˝ součet vĂ˝razĹŻ tvaru , kde buď a_i = X_i nebo a_i =; jednotlivĂĄ logickĂĄ pole se liĹĄĂ­ počtem proměnnĂ˝ch n a počtem mintermĹŻ v součtu. Na vĂ˝stupu je obvykle moĹžnĂŠ vytvořit jeĹĄtě inverzi takto vytvořenĂŠ logickĂŠ funkce, coĹž mĹŻĹže zjednoduĹĄit nĂĄvrh. ProgramovatelnĂŠ logickĂŠ pole je kombinačnĂ­ obvod, tj. odezva vĂ˝stupu PLA na změnu vstupnĂ­ch logickĂ˝ch proměnnĂ˝ch mĹŻĹže bĂ˝t podstatně rychlejĹĄĂ­ neĹž odezva systĂŠmu řízenĂŠho mikroprocesorem. Příprava logickĂŠ funkce k programovĂĄnĂ­ do PLA mĹŻĹže tak bĂ˝t příkladem pro algebraickou metodu zjednoduĹĄovĂĄnĂ­ popsanou nĂ­Ĺže.

Metody zjednoduĹĄovĂĄnĂ­ jsou v podstatě dvě: algebraickĂĄ a grafickĂĄ. PrvnĂ­ uŞívĂĄ řady identit Booleovy algebry k manipulaci s logickĂ˝mi vĂ˝razy obdobně jako se upravujĂ­ vĂ˝razy algebraickĂŠ. DruhĂĄ pouŞívĂĄ k nĂĄzornějĹĄĂ­mu zobrazenĂ­ logickĂ˝ch funkcĂ­ speciĂĄlnĂ­ch diagramĹŻ - tzv. KarnaughovĂ˝ch map, do kterĂ˝ch se zanese informace, kterou o logickĂŠ funkci vĂ­me a po ĂşpravĂĄch se z nich informace opět vybĂ­rĂĄ ve zjednoduĹĄenĂŠ formě. Obecně se dĂĄ říci, Ĺže algebraickĂĄ metoda vede rychleji k cĂ­li, vyĹžaduje vĹĄak určitou zkuĹĄenost v manipulaci s logickĂ˝mi vĂ˝razy, zatĂ­mco grafickĂŠ metody vyĹžadujĂ­ minimum předběžnĂŠ přípravy. Programy pro algebraickou manipulaci (Mathematica, Maple atd.) umoŞňujĂ­ automatizovat zjednoduĹĄovĂĄnĂ­ logickĂ˝ch vĂ˝razĹŻ. GrafickĂĄ metoda zjednoduĹĄovĂĄnĂ­, kterĂĄ by měla tuto operaci usnadnit, proto ztrĂĄcĂ­ na vĂ˝znamu. Algebraickou metodu uvĂĄdĂ­me proto, Ĺže je nĂĄzornĂ˝m příkladem vyuĹžitĂ­ identit platnĂ˝ch v Booleově algebře.

7.4.2 AlgebraickĂĄ metoda zjednoduĹĄovĂĄnĂ­

ObecnĂ˝ postup se dĂĄ charakterizovat nĂĄsledujĂ­cĂ­m zpĹŻsobem:

1. Je třeba získat Booleovský výraz pro požadovanou logickou funkci buď z popisu nebo z pravdivostní tabulky nebo ze schématu logické sítě.
2. ProvÊst vlastní zjednoduťení aplikací Booleovských identit, vytýkåním, substitucí apod.
3. Porovnat vĂ˝slednĂ˝ vztah s pĹŻvodnĂ­ pravdivostnĂ­ tabulkou.

Při provĂĄděnĂ­ Ăşprav logickĂ˝ch vĂ˝razĹŻ (ad 2) mĹŻĹžeme s vĂ˝hodou vyuŞít tabulky 7.3., kde jsou uvedeny nejdĹŻleĹžitějĹĄĂ­ identity platnĂŠ obecně v BooleovĂ˝ch algebrĂĄch.

T a b u l k a 7.3

Nejprve si vysvětlĂ­me, jakĂ˝m zpĹŻsobem si sestavĂ­me logickĂ˝ vĂ˝raz, je-li dĂĄna pravdivostnĂ­ tabulka. Obecně totiĹž mĹŻĹže bĂ˝t logickĂĄ funkce zadĂĄna tabulkou, popisem nebo zapojenĂ­m logickĂ˝ch členĹŻ. Je-li logickĂĄ funkce zadĂĄna popisem, snadno sestrojĂ­me z popisu pravdivostnĂ­ tabulku nebo přímo BooleovskĂ˝ vĂ˝raz. Pokud bychom vychĂĄzeli z danĂŠho zapojenĂ­ logickĂŠ sĂ­tě, nenĂ­ jistě sloĹžitĂŠ odvodit logickĂ˝ vĂ˝raz ze zapojenĂ­. Pokud mĂĄme pravdivostnĂ­ tabulku, překreslĂ­me ji nejprve tak, aby obsahovala jak vstupnĂ­ proměnnĂŠ, tak jejich komplementy. Pak si vĹĄĂ­mĂĄme jen řádkĹŻ, ve kterĂ˝ch mĂĄ vĂ˝sledek nabĂ˝t logickĂŠ jedničky a napĂ­ĹĄeme součin vĹĄech vstupnĂ­ch proměnnĂ˝ch nebo jejich komplementĹŻ, kterĂŠ nabĂ˝vajĂ­ v tomtĂŠĹž řádku hodnoty 1. Tento postup opakujeme pro vĹĄechny řádky, pro kterĂŠ je vĂ˝stup roven 1. Například pro 3 vstupnĂ­ logickĂŠ proměnnĂŠ mĂĄme dĂĄnu tabulku vlevo:

Tu přepíšeme užitím rovněž negovaných vstupních proměnných (vpravo):

A B C Y 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1

A B C Y 0 1 0 1 0 1 0 0 1 0 1 1 0 1 0 1 1 0 0 1 1 0 1 1 0 1 0 0 1 0 0 1 0 1 1 1 0 0 1 1 0 0 1 0 1 0 0 1 0 1 0 1 0 1 0 1

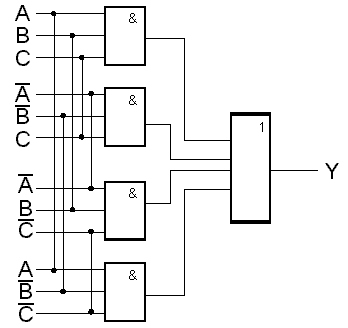
Logický obvod je znázorněn na obr. 7.25.a.

obr. 7.25a

NynĂ­ uplatnĂ­me svĂŠ znalosti identit platnĂ˝ch  Booleově algebře. Na vĂ˝raz

uplatnĂ­me zĂĄkon komutativnĂ­

vytkneme C event.

a pouĹžijeme identity

Substituce

,

zjednoduťí výraz na

.

PouĹžitĂ­m definice funkce EXCLUSIVE-OR zĂ­skĂĄme nakonec

Funkci Y tedy reprezentujĂ­ dvě hradla EXCLUSIVE-OR zapojenĂĄ v kaskĂĄdě jak je ukĂĄzĂĄno na obr. 7.25.b. Funkce Y je tĂŠĹž příkladem kombinačnĂ­ho logickĂŠho systĂŠmu.

obr. 7.25b

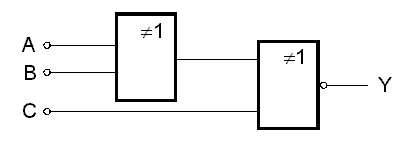
UvedenĂ˝ příklad nebyl vybrĂĄn nĂĄhodně. Reprezentuje obvod pro generaci, případně kontrolu tzv. parity. Parita je jednoduchĂ˝ zpĹŻsob odhalenĂ­ chyby při přenosu dat. ZaklĂĄdĂĄ se na předpokladu, Ĺže pravděpodobnost vĂ˝skytu chyby při přenosu je velmi malĂĄ, a pokud tedy k chybě dojde, bude pouze v jednom z přenesenĂ˝ch bitĹŻ. Kontrola paritou spočívĂĄ v přidĂĄnĂ­ dalĹĄĂ­ho, tzv. paritnĂ­ho, bitu k přenĂĄĹĄenĂ˝m bitĹŻm tak, aby celkovĂ˝ počet jedniček v přenĂĄĹĄenĂŠm slově (například bytu) spolu s paritnĂ­m bitem byl sudĂŠ nebo lichĂŠ číslo. Na přijĂ­macĂ­ straně se pak paritnĂ­ bit jednak přečte, jednak vygeneruje, a komparĂĄtorem porovnĂĄ; jsou-li oba případy stejnĂŠ, přeneslo se danĂŠ slovo sprĂĄvně (de-facto vĂ­me jen, Ĺže nenastala chyba v lichĂŠm počtu bitĹŻ, pokud by doĹĄlo k chybě ve dvou, čtyřech, atd. bitech, parita ji neodhalĂ­; proto je nutnĂ˝ předpoklad o spolehlivosti přenosu). Konstruujeme-li paritnĂ­ bit tak, aby ĹĄlo o lichĂŠ číslo, hovoříme o lichĂŠ paritě, v opačnĂŠm případě o sudĂŠ paritě. V naĹĄem případě je paritnĂ­ bit volen tak, aby celkovĂ˝ počet jedniček v danĂŠm čtyřbitovĂŠm slově byl sudĂ˝. JednĂĄ se tedy na vysĂ­lacĂ­ straně o generĂĄtor, případně, na straně přijĂ­mače, o ověřovač sudĂŠ parity. S paritou se setkĂĄvĂĄme při nastavovĂĄnĂ­ seriovĂ˝ch rozhranĂ­ osobnĂ­ho počítače, při komunikaci pomocĂ­ modemu apod.

---

---